Does Compare Mean Math Terms have you puzzled? This comprehensive guide, brought to you by COMPARE.EDU.VN, unravels the meaning of “compare” in mathematical contexts, exploring its applications and benefits. Discover how COMPARE.EDU.VN can help you make informed decisions by providing detailed analyses and evaluations, ensuring you find the best fit for your needs.
1. Understanding “Compare” in Mathematics
In mathematics, “compare” signifies determining the similarities and differences between two or more quantities, values, or mathematical objects. This involves assessing their relative magnitude, order, or characteristics to establish relationships and draw meaningful conclusions. Understanding this concept is crucial for anyone delving into mathematical problem-solving, decision-making, and analytical reasoning.
1.1. Basic Definitions and Symbols
The process of comparing in mathematics relies heavily on specific symbols and notations that convey the relationships between numbers or expressions. These symbols provide a concise and standardized way to express whether one quantity is greater than, less than, or equal to another. Here’s a rundown of the basic definitions and symbols used in mathematical comparisons:
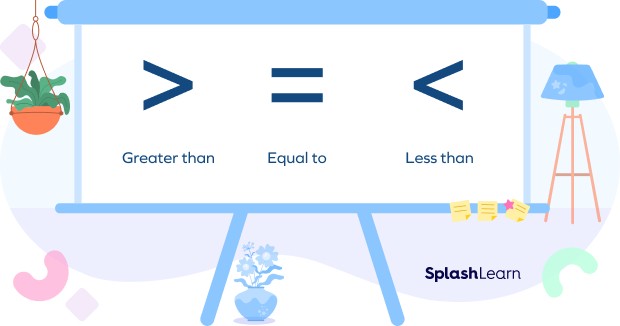
- Greater Than (>): Indicates that the value on the left side of the symbol is larger than the value on the right side. For example, 5 > 3 means 5 is greater than 3.
- Less Than (<): Indicates that the value on the left side of the symbol is smaller than the value on the right side. For example, 2 < 7 means 2 is less than 7.
- Equal To (=): Indicates that the values on both sides of the symbol are the same. For example, 4 = 4 means 4 is equal to 4.
- Greater Than or Equal To (≥): Indicates that the value on the left side of the symbol is either larger than or equal to the value on the right side. For example, x ≥ 5 means x can be 5 or any number greater than 5.
- Less Than or Equal To (≤): Indicates that the value on the left side of the symbol is either smaller than or equal to the value on the right side. For example, y ≤ 10 means y can be 10 or any number less than 10.
- Not Equal To (≠): Indicates that the values on both sides of the symbol are not the same. For example, 6 ≠ 8 means 6 is not equal to 8.
These symbols are fundamental in expressing mathematical relationships and are used across various branches of mathematics, from basic arithmetic to advanced calculus.
1.2. Comparing Numbers: A Foundational Skill
Comparing numbers is a basic yet vital skill in mathematics. It involves determining the relative size or value of two or more numbers. This skill is essential for various mathematical operations, problem-solving, and real-world applications. Here’s a more detailed explanation:
Methods for Comparing Numbers
- Number Line: A number line is a visual tool where numbers are placed in order. Numbers to the right are always greater than numbers to the left.
- Place Value: This involves comparing digits in each place value (ones, tens, hundreds, etc.). If the digits in the largest place value are the same, move to the next smaller place value until a difference is found.
- Subtraction: Subtracting one number from another can determine which is larger. If the result is positive, the first number is larger. If negative, the second number is larger. If zero, the numbers are equal.
Examples of Comparing Numbers
- Comparing Whole Numbers: To compare 456 and 523, start by looking at the hundreds place. Since 5 is greater than 4, 523 is larger.
- Comparing Decimals: To compare 3.25 and 3.4, notice that the ones place is the same. Compare the tenths place: 4 is greater than 2, so 3.4 is larger.
- Comparing Fractions: To compare 1/2 and 2/5, find a common denominator. Convert 1/2 to 5/10 and 2/5 to 4/10. Since 5 is greater than 4, 1/2 is larger.
1.3. Types of Mathematical Comparisons
Mathematical comparisons extend beyond simple numerical values. They encompass various mathematical entities, each with its own rules and methods for comparison. Here are some key types of mathematical comparisons:
- Comparing Real Numbers: Real numbers include all rational and irrational numbers. Comparison involves determining whether one number is greater than, less than, or equal to another on the number line.
- Comparing Integers: Integers are whole numbers (positive, negative, and zero). Positive integers are always greater than negative integers. For negative integers, the number with the smaller absolute value is greater.
- Comparing Fractions: Fractions can be compared by finding a common denominator or by cross-multiplication. The fraction with the larger numerator (when denominators are the same) is greater.
- Comparing Decimals: Decimals are compared by aligning the decimal points and comparing digits from left to right. If the whole number parts are the same, compare the tenths, hundredths, and so on.
- Comparing Algebraic Expressions: Algebraic expressions are compared by simplifying and then evaluating them for given values of variables. The expression with the larger value is greater.
- Comparing Sets: Sets are compared by determining whether they are equal (contain the same elements), equivalent (have the same number of elements), or whether one is a subset of the other.
- Comparing Geometric Shapes: Geometric shapes can be compared by their properties, such as area, perimeter, volume, or angles. Comparison often involves calculating these properties and then comparing the results.
2. Applications of Comparison in Mathematics
The concept of comparison is not merely theoretical; it has practical applications across various mathematical fields and real-world scenarios. From solving equations to making informed decisions, comparison plays a pivotal role.
2.1. Solving Inequalities
Inequalities in mathematics are statements that compare two expressions using symbols like >, <, ≥, or ≤. Solving inequalities involves finding the range of values that satisfy the given comparison. This process is fundamental in algebra and calculus and has wide-ranging applications.
Basic Principles of Solving Inequalities:
- Addition/Subtraction: Adding or subtracting the same number from both sides of an inequality does not change the direction of the inequality.
- Multiplication/Division by a Positive Number: Multiplying or dividing both sides of an inequality by a positive number does not change the direction of the inequality.
- Multiplication/Division by a Negative Number: Multiplying or dividing both sides of an inequality by a negative number reverses the direction of the inequality.
Examples of Solving Inequalities:
-
Example 1: Solve (x + 3 > 5)
Subtract 3 from both sides:
(x + 3 – 3 > 5 – 3)
(x > 2)
-
Example 2: Solve (2x – 1 leq 7)
Add 1 to both sides:
(2x – 1 + 1 leq 7 + 1)
(2x leq 8)
Divide both sides by 2:
(x leq 4)
-
Example 3: Solve (-3x + 4 < 10)
Subtract 4 from both sides:
(-3x < 6)
Divide both sides by -3 (and reverse the inequality):
(x > -2)
2.2. Optimization Problems
Optimization problems involve finding the best solution from a set of possible solutions. This often requires comparing different scenarios to identify the maximum or minimum value of a function. Calculus and linear programming are key tools in solving optimization problems.
Optimization Techniques:
- Calculus: In calculus, optimization involves finding critical points of a function by setting its derivative equal to zero. The second derivative test is then used to determine whether each critical point is a maximum, minimum, or saddle point.
- Linear Programming: This technique is used to optimize a linear objective function subject to linear constraints. The feasible region is determined by the constraints, and the optimal solution lies at one of the vertices of this region.
Examples of Optimization Problems:
-
Example 1: Maximize Profit
A company wants to maximize its profit by producing two products, A and B. The profit function is (P = 3x + 5y), where (x) is the number of units of product A and (y) is the number of units of product B. The production is subject to the constraints (x + y leq 100) and (2x + y leq 150). Using linear programming, the company can determine the optimal number of units of each product to maximize profit.
-
Example 2: Minimize Cost
A farmer wants to minimize the cost of feeding his livestock. He needs to provide a certain amount of nutrients, which can be obtained from two types of feed. The cost function is (C = 2x + 3y), where (x) is the amount of feed type 1 and (y) is the amount of feed type 2. The nutrient requirements impose constraints on the amounts of each feed type. The farmer can use linear programming to find the optimal amounts of each feed to minimize cost while meeting nutrient requirements.
2.3. Statistical Analysis
In statistical analysis, comparison is used to assess the differences between data sets, groups, or variables. This involves using statistical tests to determine whether observed differences are significant or due to chance.
Common Statistical Comparison Techniques:
- T-Tests: Used to compare the means of two groups to determine if there is a significant difference.
- ANOVA (Analysis of Variance): Used to compare the means of three or more groups to determine if there is a significant difference.
- Chi-Square Tests: Used to compare categorical data to determine if there is a significant association between variables.
- Regression Analysis: Used to model the relationship between a dependent variable and one or more independent variables, allowing for comparisons of the effects of different variables.
Examples of Statistical Comparison:
-
Example 1: Comparing Test Scores
A teacher wants to compare the test scores of two classes. She uses a t-test to determine if the mean scores of the two classes are significantly different.
-
Example 2: Comparing Treatment Effects
A researcher wants to compare the effectiveness of three different treatments for a medical condition. He uses ANOVA to determine if there is a significant difference in the outcomes of the three treatments.
-
Example 3: Analyzing Survey Data
An analyst wants to determine if there is an association between gender and preference for a particular product. He uses a chi-square test to analyze the survey data.
3. Real-World Applications of Mathematical Comparison
Mathematical comparison is not confined to the classroom or academic research; it is a ubiquitous tool in everyday life and various professional fields.
3.1. Financial Decisions
Making informed financial decisions often involves comparing different options to maximize returns or minimize costs. Whether it’s choosing between investment opportunities or comparing loan options, mathematical comparison is essential.
Examples in Financial Decisions:
- Investment Options: Comparing the potential returns, risks, and fees associated with different investment opportunities, such as stocks, bonds, and mutual funds.
- Loan Options: Comparing interest rates, repayment terms, and fees for different loan options, such as mortgages, auto loans, and personal loans.
- Budgeting: Comparing income and expenses to ensure financial stability and identify areas for potential savings.
- Insurance Plans: Comparing premiums, coverage, and deductibles for different insurance plans to find the best value for your needs.
3.2. Consumer Choices
Consumers routinely use comparison to make purchasing decisions, assessing factors such as price, quality, features, and reviews to determine the best value.
Examples in Consumer Choices:
- Electronics: Comparing the features, specifications, and prices of different smartphones, laptops, or televisions to find the best option.
- Appliances: Comparing the energy efficiency, capacity, and features of different refrigerators, washing machines, or ovens.
- Cars: Comparing the fuel efficiency, safety ratings, and features of different car models to make an informed purchase.
- Services: Comparing the prices, terms, and reviews of different service providers, such as internet, phone, or cable companies.
3.3. Business Strategy
Businesses use comparison to analyze market trends, assess competitor performance, and make strategic decisions that drive growth and profitability.
Examples in Business Strategy:
- Market Analysis: Comparing market trends, consumer preferences, and competitor strategies to identify opportunities and threats.
- Performance Metrics: Comparing key performance indicators (KPIs) such as sales, revenue, and customer satisfaction to track progress and identify areas for improvement.
- Investment Decisions: Comparing the potential returns, costs, and risks of different investment opportunities, such as new product development, market expansion, or mergers and acquisitions.
- Pricing Strategies: Comparing the pricing strategies of competitors to determine the optimal pricing for products and services.
4. Strategies for Effective Mathematical Comparison
To ensure accurate and meaningful mathematical comparisons, it’s important to follow a structured approach. Here are some strategies for effective comparison:
4.1. Define the Criteria
Clearly define the criteria for comparison to ensure that the analysis is focused and relevant. This involves identifying the key factors or characteristics that will be used to evaluate the options.
Steps for Defining Criteria:
- Identify the Objectives: Determine the goals or objectives of the comparison. What are you trying to achieve or evaluate?
- List the Factors: List all the factors or characteristics that are relevant to the comparison. These could include numerical values, qualitative features, or performance metrics.
- Prioritize the Factors: Prioritize the factors based on their importance. Some factors may be more critical than others in achieving the objectives.
- Define Measurement Metrics: Define how each factor will be measured or evaluated. This could involve using specific units, scales, or ratings.
4.2. Use Standardized Metrics
Standardized metrics provide a consistent and objective basis for comparison, reducing bias and ensuring accuracy.
Examples of Standardized Metrics:
- Units of Measurement: Use consistent units of measurement for all values being compared. For example, use meters instead of feet when comparing lengths.
- Scales and Ratings: Use standardized scales or ratings for qualitative factors. For example, use a Likert scale (1-5) to rate customer satisfaction.
- Financial Ratios: Use standardized financial ratios, such as return on investment (ROI) or debt-to-equity ratio, to compare the financial performance of different companies.
4.3. Consider Context
Always consider the context in which the comparison is being made. This includes understanding the assumptions, limitations, and potential biases that could influence the results.
Factors to Consider:
- Assumptions: Identify any assumptions that are being made in the comparison. Are these assumptions valid and reasonable?
- Limitations: Recognize any limitations of the data or methods being used. Are there any factors that are not being taken into account?
- Biases: Be aware of potential biases that could influence the results. Are there any subjective factors that could skew the comparison?
- External Factors: Consider any external factors that could affect the comparison, such as market conditions, regulatory changes, or technological advancements.
5. Common Pitfalls to Avoid
Even with a structured approach, there are common pitfalls that can undermine the accuracy and validity of mathematical comparisons. Being aware of these pitfalls can help you avoid them.
5.1. Apples to Oranges
Comparing dissimilar items or values without proper adjustment can lead to misleading conclusions. Make sure you are comparing like with like.
Strategies to Avoid:
- Standardize the Metrics: Use standardized metrics that allow for a fair comparison between dissimilar items.
- Adjust for Differences: Adjust the values to account for any significant differences between the items being compared.
- Focus on Relevant Factors: Focus on the factors that are most relevant to the comparison and ignore irrelevant differences.
5.2. Ignoring Scale
Failing to account for differences in scale can distort the comparison and lead to incorrect interpretations.
Strategies to Avoid:
- Use Relative Measures: Use relative measures, such as percentages or ratios, to compare values that are on different scales.
- Normalize the Data: Normalize the data by scaling the values to a common range, such as 0 to 1.
- Use Logarithmic Scales: Use logarithmic scales to compare values that vary over several orders of magnitude.
5.3. Confirmation Bias
Seeking out information that confirms pre-existing beliefs while ignoring contradictory evidence can undermine objectivity and lead to biased comparisons.
Strategies to Avoid:
- Seek Diverse Information: Actively seek out information from a variety of sources, including those that may challenge your pre-existing beliefs.
- Be Open to Changing Your Mind: Be open to changing your mind if the evidence supports a different conclusion.
- Use Objective Criteria: Use objective criteria for evaluating the information and avoid relying on subjective opinions or feelings.
6. Tools and Resources for Mathematical Comparison
A variety of tools and resources can assist in performing mathematical comparisons, from simple calculators to sophisticated software.
6.1. Calculators and Spreadsheets
Basic calculators and spreadsheet software like Microsoft Excel or Google Sheets can be used for simple numerical comparisons.
How to Use Calculators and Spreadsheets:
- Perform Basic Calculations: Use calculators to perform basic arithmetic operations, such as addition, subtraction, multiplication, and division.
- Create Tables and Charts: Use spreadsheets to create tables and charts that visualize the data and make it easier to compare.
- Use Formulas and Functions: Use formulas and functions to perform more complex calculations, such as calculating percentages, averages, and standard deviations.
6.2. Statistical Software
Statistical software packages like SPSS, SAS, or R provide advanced tools for statistical analysis and comparison.
Features of Statistical Software:
- Statistical Tests: Perform a wide range of statistical tests, such as t-tests, ANOVA, and chi-square tests.
- Regression Analysis: Conduct regression analysis to model the relationship between variables and compare the effects of different variables.
- Data Visualization: Create sophisticated data visualizations, such as histograms, scatter plots, and box plots.
6.3. Online Comparison Tools
Numerous online comparison tools are available for comparing products, services, and other options.
Examples of Online Comparison Tools:
- Product Comparison Websites: Websites that allow you to compare the features, prices, and reviews of different products.
- Financial Comparison Websites: Websites that allow you to compare interest rates, fees, and terms for different financial products, such as loans and credit cards.
- Service Comparison Websites: Websites that allow you to compare the prices, terms, and reviews of different service providers, such as internet, phone, and cable companies.
7. COMPARE.EDU.VN: Your Partner in Informed Decision-Making
At COMPARE.EDU.VN, we understand the importance of making informed decisions. Our website is designed to provide you with comprehensive comparisons across a wide range of topics, from educational programs to consumer products.
7.1. Comprehensive Comparisons
We offer detailed comparisons that cover all the essential aspects of the options you are considering. Our comparisons are based on thorough research and objective analysis, ensuring that you have all the information you need to make the right choice.
Features of Our Comparisons:
- Detailed Analysis: We provide a detailed analysis of each option, covering its strengths, weaknesses, features, and benefits.
- Objective Evaluation: Our evaluations are based on objective criteria and data, ensuring that you receive an unbiased assessment.
- Up-to-Date Information: We keep our information up-to-date to ensure that you have the latest data and insights.
7.2. User-Friendly Interface
Our website features a user-friendly interface that makes it easy to find and compare the information you need. You can quickly search for specific topics, filter the results based on your preferences, and view the comparisons in a clear and concise format.
Benefits of Our User-Friendly Interface:
- Easy Navigation: Our website is easy to navigate, allowing you to quickly find the information you need.
- Clear Presentation: We present the comparisons in a clear and concise format, making it easy to understand the key differences between the options.
- Customizable Filters: You can customize the filters to focus on the factors that are most important to you.
7.3. Wide Range of Topics
Whether you’re comparing educational programs, consumer products, or financial services, COMPARE.EDU.VN has you covered. We offer comparisons across a wide range of topics, ensuring that you can find the information you need to make informed decisions.
Examples of Topics We Cover:
- Education: Compare universities, colleges, and online courses to find the best fit for your academic goals.
- Consumer Products: Compare electronics, appliances, and other consumer products to find the best value for your money.
- Financial Services: Compare loans, credit cards, and investment options to make informed financial decisions.
- Software and Technology: Compare software applications, cloud services, and other technology solutions to find the best tools for your needs.
8. FAQs About Mathematical Comparisons
8.1. Why is comparing numbers important in our daily lives?
Comparing numbers is important in our daily lives because it helps us make informed decisions. Whether it’s comparing prices at the grocery store, evaluating loan options, or assessing different job offers, the ability to compare numbers allows us to make choices that align with our goals and values.
8.2. How is comparing numbers different from ordering numbers?
Comparing numbers involves determining the relative size or value of two or more numbers. Ordering numbers, on the other hand, involves arranging a set of numbers in a specific sequence, such as ascending or descending order. While comparing numbers focuses on pairwise relationships, ordering numbers focuses on the overall sequence.
8.3. What is the quick way for comparing numbers?
The quickest way to compare numbers depends on the context. For whole numbers, you can start by comparing the number of digits. For decimals, you can align the decimal points and compare the digits from left to right. For fractions, you can find a common denominator and compare the numerators.
8.4. How do you compare rational numbers?
Comparing rational numbers is similar to comparing fractions. You can find a common denominator and compare the numerators. Alternatively, you can convert the rational numbers to decimals and compare the decimal values.
8.5. What are some common mistakes when comparing numbers?
Some common mistakes when comparing numbers include comparing dissimilar items, ignoring scale, and confirmation bias. To avoid these mistakes, it’s important to define the criteria, use standardized metrics, consider the context, and seek diverse information.
9. Conclusion: Empowering Your Decisions with COMPARE.EDU.VN
Understanding “compare” in math terms is essential for informed decision-making in various aspects of life. By mastering the strategies and avoiding common pitfalls, you can make accurate and meaningful comparisons that lead to better outcomes.
Don’t let the complexity of choices overwhelm you. Visit COMPARE.EDU.VN at 333 Comparison Plaza, Choice City, CA 90210, United States or contact us via Whatsapp at +1 (626) 555-9090, and let us help you navigate the world of comparisons with confidence. Whether you’re a student, a consumer, or a professional, compare.edu.vn is your trusted partner in making smart, well-informed decisions. Start exploring today and discover the power of comparison!