Unlocking insights into complex data analysis, post hoc comparisons are vital for understanding relationships between variables. COMPARE.EDU.VN is your go-to source for mastering these comparisons, offering comprehensive resources and expert guidance. Delve into the nuances of post hoc analysis and make data-driven decisions with confidence, exploring related concepts like ANOVA and statistical significance to enhance your analytical skills.
1. What Are Post Hoc Comparisons and Why Are They Important?
Post hoc comparisons, also known as post-hoc tests or multiple comparison procedures, are statistical tests conducted after a significant result has been obtained from an Analysis of Variance (ANOVA) test. They are essential for determining exactly which groups differ significantly from each other.
1.1. Why Are Post Hoc Comparisons Necessary?
- Specificity: ANOVA tells us if there’s a significant difference somewhere among the group means, but not where the differences lie. Post hoc tests pinpoint those specific differences.
- Controlling Type I Error: Performing multiple t-tests to compare all possible pairs of groups inflates the risk of committing a Type I error (false positive). Post hoc tests control for this increased risk.
- Avoiding Misinterpretation: Without post hoc tests, interpreting ANOVA results can be misleading, leading to inaccurate conclusions.
1.2. Key Concepts Related to Post Hoc Comparisons
- ANOVA (Analysis of Variance): A statistical test that compares the means of two or more groups. Factorial ANOVA extends this to multiple independent variables.
- Type I Error (False Positive): Rejecting the null hypothesis when it is actually true.
- Familywise Error Rate: The probability of making at least one Type I error when performing multiple hypothesis tests.
- Statistical Significance: A result is statistically significant if it is unlikely to have occurred by chance.
- Dependent Variable: The variable being measured or tested in an experiment.
- Independent Variable: The variable that is manipulated or changed in an experiment.
2. Understanding the Role of Post Hoc Tests in ANOVA
Post hoc tests are an integral part of ANOVA when dealing with more than two groups. They help refine the broad conclusions of ANOVA into specific, actionable insights.
2.1. The ANOVA Foundation
ANOVA is used to determine if there are any statistically significant differences between the means of two or more independent groups. The null hypothesis in ANOVA is that all group means are equal.
Example: Imagine a study comparing the effectiveness of three different teaching methods on student test scores. ANOVA can tell us if there is a significant difference in test scores across the three methods.
2.2. Why Not Just Use Multiple T-Tests?
While t-tests can compare the means of two groups, using multiple t-tests after ANOVA is problematic. Each t-test carries a risk of a Type I error (typically 5%). When conducting multiple t-tests, the overall probability of making at least one Type I error increases, leading to a higher chance of false positives.
2.3. Post Hoc Tests to the Rescue
Post hoc tests are designed to control the familywise error rate, ensuring that the overall risk of making a Type I error across all comparisons remains at the desired level (usually 5%).
Example: In the teaching method study, post hoc tests would compare Method A vs. Method B, Method A vs. Method C, and Method B vs. Method C, all while controlling for the inflated risk of Type I error.
3. Do Post Hoc Comparisons Compare Between Dependent Variables?
No, post hoc comparisons do not compare between dependent variables. They are designed to compare the means of different groups within a single dependent variable after an ANOVA test has shown a significant difference. Let’s break this down:
- Dependent Variable Focus: Post hoc tests operate within the context of a single dependent variable. They analyze how the means of this variable differ across various groups defined by one or more independent variables.
- Group Comparisons: The core purpose of post hoc tests is to identify which specific pairs of groups have significantly different means for the dependent variable.
Analogy: Imagine you’re analyzing the effect of different fertilizers (independent variable) on plant height (dependent variable). Post hoc tests would tell you which fertilizers resulted in significantly different plant heights compared to each other.
3.1. Clarifying the Misconception
It’s important to distinguish between:
- Post Hoc Tests: Compare group means within a single dependent variable.
- Multivariate Analysis (MANOVA): Compares groups across multiple dependent variables simultaneously.
If your research question involves comparing groups across multiple dependent variables, MANOVA is the appropriate statistical method, not post hoc tests.
3.2. Examples to Illustrate the Point
-
Scenario 1: Comparing Exam Scores:
- Dependent Variable: Exam Score (one variable)
- Independent Variable: Study Method (e.g., Group A, Group B, Group C)
- Post Hoc Tests: Determine which study methods led to significantly different exam scores.
-
Scenario 2: Comparing Plant Growth:
- Dependent Variable: Plant Height (one variable)
- Independent Variable: Fertilizer Type (e.g., Fertilizer X, Fertilizer Y, Control)
- Post Hoc Tests: Determine which fertilizer types resulted in significantly different plant heights.
In both scenarios, post hoc tests are used to compare group means for a single dependent variable.
4. Common Types of Post Hoc Tests
Several post hoc tests are available, each with its own strengths and weaknesses. The choice of test depends on the specific research question and the characteristics of the data.
4.1. Popular Post Hoc Tests
- Tukey’s Honestly Significant Difference (HSD): A widely used test that provides a good balance between power and control of Type I error. It is particularly suitable when all pairwise comparisons are of interest.
- Bonferroni Correction: A conservative method that adjusts the significance level for each comparison. It is simple to apply but can be overly conservative, especially with a large number of comparisons.
- Scheffé’s Method: The most conservative post hoc test, suitable for complex comparisons beyond pairwise comparisons. It has low power but provides strong control of Type I error.
- Newman-Keuls: A stepwise procedure that compares means in order of magnitude. It has more power than Tukey’s HSD but less control of Type I error.
- Dunnett’s Test: Used when comparing multiple treatment groups to a single control group.
- Fisher’s Least Significant Difference (LSD): The least conservative test, equivalent to performing multiple t-tests without correction. It has the highest power but the poorest control of Type I error and should only be used with caution.
4.2. Choosing the Right Test
- Equal Variances Assumed: If the variances of the groups are approximately equal, Tukey’s HSD or Newman-Keuls are good choices.
- Unequal Variances: If the variances are unequal, consider using Games-Howell.
- Specific Comparisons: If you have specific comparisons in mind, Dunnett’s test may be appropriate.
- Conservative Approach: If controlling Type I error is paramount, Bonferroni or Scheffé’s method are suitable, albeit at the cost of reduced power.
5. How to Perform Post Hoc Tests
Post hoc tests are typically performed using statistical software packages such as SPSS, R, or SAS. The specific steps vary depending on the software and the chosen post hoc test.
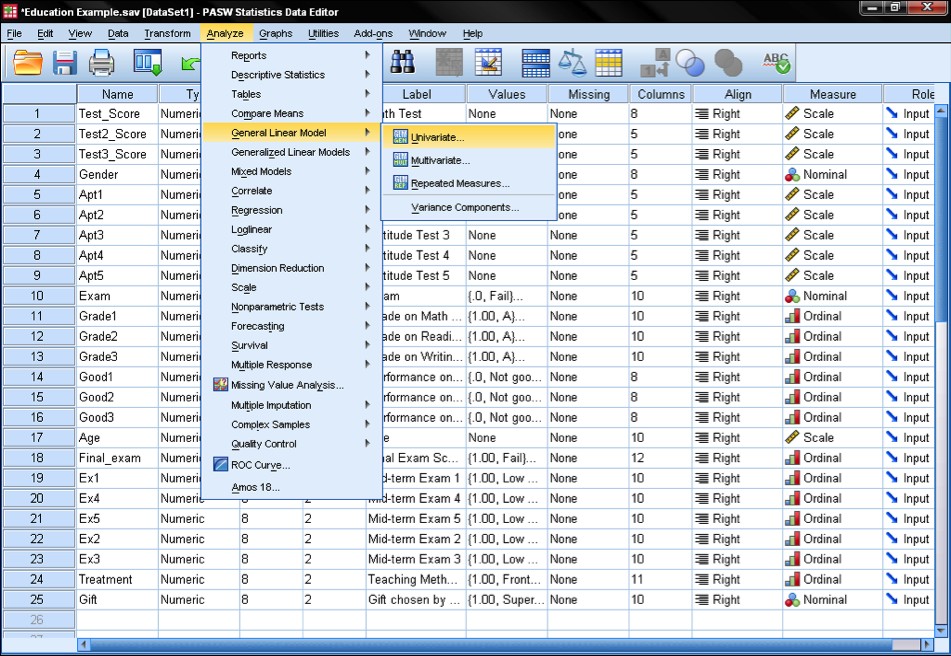
5.1. Post Hoc Tests in SPSS
- Run ANOVA: Perform the ANOVA test in SPSS.
- Specify Post Hoc Tests: In the ANOVA dialog box, select the “Post Hoc” option.
- Choose Test(s): Select the desired post hoc test(s) from the list.
- Run Analysis: Execute the analysis.
- Interpret Results: SPSS will output tables showing the pairwise comparisons, p-values, and significance levels.
5.2. Interpreting Post Hoc Results
- P-Value: The p-value indicates the probability of observing the data if there is no true difference between the group means. A p-value less than the chosen significance level (e.g., 0.05) indicates a statistically significant difference.
- Significance Level: The threshold for determining statistical significance (typically 0.05).
- Pairwise Comparisons: The post hoc test output will show the results of each pairwise comparison between the groups.
Example: If Tukey’s HSD test shows a significant difference between Group A and Group B (p < 0.05), it means that the means of these two groups are significantly different from each other.
6. Real-World Applications of Post Hoc Comparisons
Post hoc comparisons are used in a wide range of fields to analyze data and draw meaningful conclusions.
6.1. Examples Across Disciplines
- Medicine: Comparing the effectiveness of different treatments for a disease.
- Education: Evaluating the impact of various teaching methods on student performance.
- Marketing: Analyzing the effectiveness of different advertising campaigns.
- Psychology: Investigating the effects of various therapies on mental health.
- Agriculture: Comparing the yields of different crop varieties.
6.2. Case Study: A Marketing Example
A marketing team wants to compare the effectiveness of four different advertising campaigns on sales. They run an ANOVA and find a significant difference in sales across the campaigns. To determine which campaigns are significantly different from each other, they perform Tukey’s HSD post hoc test.
The results show that Campaign A significantly outperformed Campaign B and Campaign C, but not Campaign D. This information helps the marketing team focus their efforts on the most effective campaigns.
7. Advantages and Disadvantages of Post Hoc Comparisons
Like any statistical method, post hoc comparisons have their advantages and disadvantages.
7.1. Advantages
- Specificity: Pinpoint which groups differ significantly.
- Type I Error Control: Control the familywise error rate.
- Meaningful Insights: Provide more detailed and actionable insights than ANOVA alone.
7.2. Disadvantages
- Complexity: Can be complex to choose the appropriate test and interpret the results.
- Reduced Power: Some tests can be conservative and have reduced power.
- Misinterpretation: Potential for misinterpretation if not used correctly.
8. Common Mistakes to Avoid When Using Post Hoc Comparisons
Avoiding common pitfalls can ensure accurate and reliable results.
8.1. Mistakes to Watch Out For
- Using Without Significant ANOVA: Performing post hoc tests when the initial ANOVA is not significant.
- Choosing the Wrong Test: Selecting a post hoc test that is not appropriate for the data.
- Misinterpreting Results: Misinterpreting the p-values and significance levels.
- Ignoring Assumptions: Ignoring the assumptions of the post hoc tests.
8.2. Best Practices
- Run ANOVA First: Always perform ANOVA before conducting post hoc tests.
- Check Assumptions: Ensure that the assumptions of the ANOVA and post hoc tests are met.
- Choose Wisely: Select the most appropriate post hoc test based on the research question and data characteristics.
- Interpret Carefully: Carefully interpret the results and consider the limitations of the tests.
9. The Future of Post Hoc Comparisons
Statistical methods are continuously evolving, and post hoc comparisons are no exception.
9.1. Emerging Trends
- Bayesian Approaches: Bayesian methods are gaining popularity for post hoc comparisons.
- Non-Parametric Tests: Non-parametric post hoc tests are being developed for data that do not meet the assumptions of parametric tests.
- Adaptive Methods: Adaptive methods that adjust the significance level based on the data are being explored.
9.2. The Role of Technology
Statistical software is becoming more user-friendly, making it easier to perform and interpret post hoc tests. Advanced visualization techniques are also helping researchers to better understand the results.
10. FAQ About Post Hoc Comparisons
10.1. When should I use post hoc tests?
Use post hoc tests after you have run an ANOVA and found a statistically significant difference between the means of your groups. They help you determine which specific groups differ significantly from each other.
10.2. What is the difference between ANOVA and post hoc tests?
ANOVA tells you if there is a significant difference somewhere between the means of two or more groups. Post hoc tests tell you exactly where those differences lie.
10.3. Why can’t I just use multiple t-tests instead of post hoc tests?
Performing multiple t-tests inflates the risk of committing a Type I error (false positive). Post hoc tests control for this increased risk.
10.4. Which post hoc test should I use?
The choice of post hoc test depends on the specific research question and the characteristics of the data. Common options include Tukey’s HSD, Bonferroni correction, Scheffé’s method, Newman-Keuls, and Dunnett’s test.
10.5. What does a significant p-value in a post hoc test mean?
A significant p-value (typically p < 0.05) in a post hoc test indicates that there is a statistically significant difference between the means of the two groups being compared.
10.6. Can I use post hoc tests if my data is not normally distributed?
If your data is not normally distributed, you may need to use non-parametric alternatives to ANOVA and post hoc tests.
10.7. Are post hoc tests used to compare dependent variables?
No, post hoc tests are used to compare the means of different groups within a single dependent variable. If you want to compare groups across multiple dependent variables, you should use MANOVA.
10.8. What is the familywise error rate?
The familywise error rate is the probability of making at least one Type I error when performing multiple hypothesis tests. Post hoc tests are designed to control this rate.
10.9. How do I interpret the results of post hoc tests?
Carefully examine the p-values and significance levels for each pairwise comparison. If the p-value is less than the chosen significance level, the difference between the group means is statistically significant.
10.10. Where can I learn more about post hoc tests?
COMPARE.EDU.VN offers a wealth of resources and expert guidance on post hoc comparisons and other statistical methods. Visit our website to explore our comprehensive content and enhance your data analysis skills.
Unlock the Power of Post Hoc Comparisons with COMPARE.EDU.VN
Post hoc comparisons are a powerful tool for analyzing data and drawing meaningful conclusions. By understanding the principles and techniques discussed in this article, you can effectively use post hoc tests to gain deeper insights from your data.
Don’t struggle with complex statistical comparisons. Visit COMPARE.EDU.VN today for comprehensive resources, expert guidance, and easy-to-understand explanations. Make data-driven decisions with confidence and unlock the full potential of your research.
Ready to take your data analysis skills to the next level?
Visit COMPARE.EDU.VN now and explore our comprehensive collection of articles, tutorials, and expert insights on post hoc comparisons and other essential statistical methods.
Address: 333 Comparison Plaza, Choice City, CA 90210, United States.
Whatsapp: +1 (626) 555-9090.
Website: compare.edu.vn.
Illustration of the GLM procedure dialog in SPSS, showcasing the specification of a full-factorial model with “Math Test” as the dependent variable and “Exam” and “Gender” as independent variables, highlighting the settings for statistical analysis.
Visualization of the Post Hoc Tests dialog box in SPSS, emphasizing the configuration options for conducting separate comparisons between factor levels, specifically highlighting the Student-Newman-Keuls (SNK) test for improved reliability in post hoc comparison by increasing sample size.