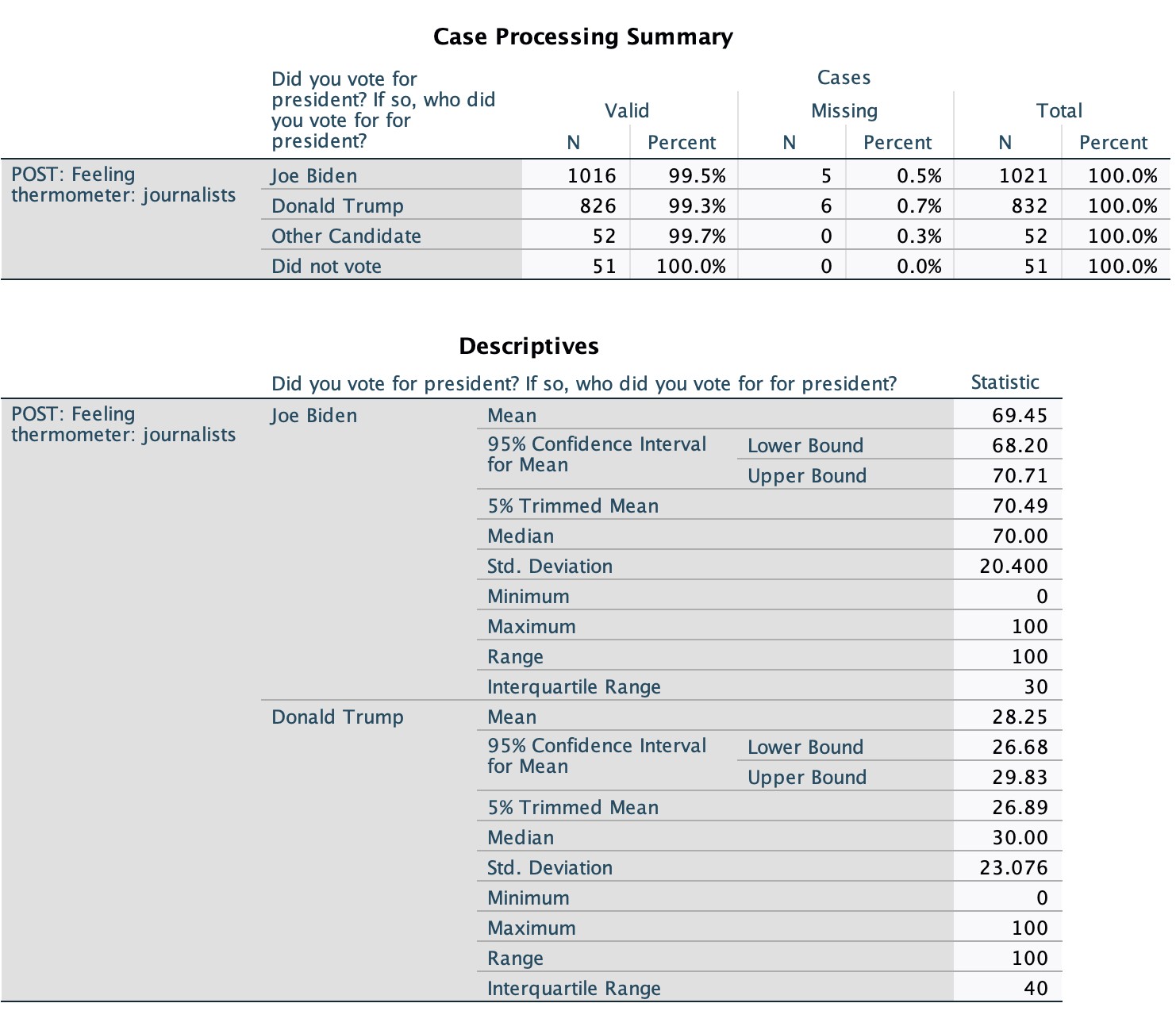
Confidence intervals are essential statistical tools, but Can We Compare Confidence Intervals effectively? Yes, confidence intervals can be compared to determine if there are statistically significant differences between the means of two or more populations. At COMPARE.EDU.VN, we provide a comprehensive guide on how to interpret and utilize confidence intervals for meaningful data analysis. Understanding the nuances of confidence interval comparisons is crucial for making informed decisions and drawing accurate conclusions from research data.
1. What Is A Confidence Interval And Why Is It Important?
A confidence interval is a range of values that estimates an unknown population parameter with a certain level of confidence. The confidence level represents the percentage of times that the interval would contain the true population parameter if the same population were sampled repeatedly. Confidence intervals are vital because they provide more information than a single point estimate, offering a range of plausible values and an indication of the precision of the estimate.
1.1 Definition Of A Confidence Interval
A confidence interval is a range of values, calculated from sample data, that is likely to contain the true value of an unknown population parameter. It is associated with a confidence level, which specifies the probability that the interval contains the true parameter.
- Example: A 95% confidence interval for the mean height of adult women might be 5’4” to 5’6”. This means we are 95% confident that the true average height of all adult women falls within this range.
1.2 Key Components Of A Confidence Interval
Understanding the key components helps in the accurate interpretation of confidence intervals.
- Sample Statistic: This is the point estimate calculated from the sample data (e.g., sample mean).
- Margin of Error: This value accounts for the uncertainty in the sample estimate. It is calculated using the standard error and a critical value.
- Confidence Level: The probability that the interval contains the true population parameter (e.g., 95%, 99%).
- Standard Error: A measure of the statistical accuracy of an estimate, equal to the standard deviation of the theoretical distribution of a large population of such estimates.
1.3 Importance Of Confidence Intervals In Statistical Analysis
Confidence intervals are invaluable in statistical analysis for several reasons:
- Precision of Estimates: They provide a range of plausible values, indicating the precision of the estimate. A narrow interval suggests higher precision.
- Hypothesis Testing: Confidence intervals can be used to perform hypothesis tests. If the interval does not contain the null hypothesis value, the null hypothesis can be rejected.
- Decision Making: They assist in making informed decisions by providing a range of likely outcomes.
- Comparing Groups: Confidence intervals can be compared to assess whether the differences between group means are statistically significant.
2. Understanding The Basics Of Confidence Interval Comparison
Comparing confidence intervals involves determining whether the ranges of the intervals overlap and assessing the magnitude of the difference between the point estimates. The goal is to ascertain if the observed differences are statistically significant or simply due to random variation.
2.1 What Does It Mean To Compare Confidence Intervals?
Comparing confidence intervals means assessing whether the ranges of two or more intervals overlap and evaluating the practical significance of any observed differences. It helps determine if the underlying population parameters are truly different.
- Example: If the 95% confidence interval for the average test score of Class A is 70-75, and for Class B is 72-78, comparing these intervals helps determine if there is a significant difference in the average performance of the two classes.
2.2 Key Principles For Comparing Confidence Intervals
Several key principles guide the comparison of confidence intervals:
- Overlap: The extent to which confidence intervals overlap is a primary indicator of potential differences. Non-overlapping intervals suggest a significant difference.
- Magnitude of Difference: Consider the size of the difference between the point estimates relative to the margin of error. A large difference indicates a more substantial effect.
- Confidence Level: Ensure the confidence levels are the same when comparing intervals. For instance, comparing two 95% confidence intervals provides a consistent basis.
- Sample Size: Larger sample sizes generally result in narrower confidence intervals, providing more precise estimates and more reliable comparisons.
2.3 Common Mistakes To Avoid When Comparing Confidence Intervals
Avoiding common mistakes ensures accurate interpretation of comparisons:
- Ignoring the Margin of Error: Focus not only on the point estimates but also on the margin of error, which reflects the uncertainty in the estimate.
- Assuming Non-Overlap Always Indicates Significance: While non-overlap often suggests significance, it is not a definitive rule. Further statistical tests might be necessary.
- Forgetting the Context: Always consider the context of the data and the practical implications of the findings.
- Equating Statistical Significance with Practical Significance: A statistically significant difference may not always be practically important in real-world applications.
3. Scenarios Where Comparing Confidence Intervals Is Useful
Confidence interval comparisons are valuable in various scenarios across different fields, helping to make informed decisions based on data analysis.
3.1 Comparing Means Of Two Independent Groups
One of the most common uses is to compare the means of two independent groups to determine if there is a statistically significant difference between them.
- Example: A pharmaceutical company might compare the effectiveness of a new drug against a placebo. Confidence intervals for the mean improvement in symptoms for each group can be compared.
3.2 Comparing Proportions Of Two Populations
Confidence intervals can be used to compare proportions, helping to determine if there is a significant difference in the occurrence of a certain characteristic in two populations.
- Example: A political analyst might compare the proportion of voters who support a particular candidate in two different demographic groups.
3.3 Monitoring Changes Over Time
By comparing confidence intervals at different time points, it is possible to monitor changes in a variable over time and assess whether these changes are statistically significant.
- Example: An environmental agency might monitor changes in air quality by comparing confidence intervals for pollution levels at different times of the year.
3.4 Assessing The Impact Of Interventions
Confidence intervals can be used to assess the impact of interventions by comparing the outcomes before and after the intervention.
- Example: A school district might assess the impact of a new teaching method by comparing confidence intervals for student test scores before and after the implementation of the method.
4. Techniques For Comparing Confidence Intervals
Several techniques can be used to compare confidence intervals effectively, each with its own strengths and applications.
4.1 Visual Inspection Of Overlap
A simple method is to visually inspect whether the confidence intervals overlap. Non-overlapping intervals suggest a statistically significant difference, while overlapping intervals indicate the difference may not be significant.
- Example: If the 95% confidence interval for the mean score of Group A is [10, 15] and for Group B is [16, 20], the non-overlapping intervals suggest a significant difference between the means of the two groups.
4.2 Calculating The Difference Between Means And Its Confidence Interval
Another technique involves calculating the difference between the means of two groups and constructing a confidence interval for this difference. If the confidence interval for the difference does not include zero, the difference is statistically significant.
- Example: Suppose the mean test score for Group A is 75 with a 95% confidence interval of [70, 80], and for Group B is 82 with a 95% confidence interval of [77, 87]. The difference in means is 7, and if the 95% confidence interval for this difference does not include zero, it suggests a significant difference.
4.3 Using Hypothesis Tests In Conjunction With Confidence Intervals
Hypothesis tests can be used in conjunction with confidence intervals to provide a more rigorous assessment of statistical significance. The confidence interval can be used to estimate the effect size, while the hypothesis test provides a p-value to assess the strength of the evidence against the null hypothesis.
- Example: Perform a t-test to compare the means of two groups. If the p-value is less than 0.05 and the confidence interval for the difference in means does not include zero, there is strong evidence of a significant difference.
4.4 Effect Size And Practical Significance
In addition to statistical significance, it is important to consider the effect size and practical significance of the findings. Effect size measures the magnitude of the difference between groups, while practical significance refers to whether the difference is meaningful in a real-world context.
- Example: Even if a study finds a statistically significant difference in test scores between two teaching methods, the difference might be small (e.g., a 2-point difference on a 100-point scale). This difference might not be practically significant if the new teaching method is more expensive or difficult to implement.
5. Factors Affecting The Width Of Confidence Intervals
Several factors influence the width of confidence intervals, which in turn affects the precision of the estimates and the ability to detect significant differences.
5.1 Sample Size
Larger sample sizes generally lead to narrower confidence intervals because they provide more information about the population.
- Explanation: As the sample size increases, the standard error decreases, which reduces the margin of error and narrows the confidence interval.
- Example: A study with 1000 participants will generally produce a narrower confidence interval than a study with 100 participants, assuming all other factors are equal.
5.2 Confidence Level
Higher confidence levels (e.g., 99% vs. 95%) result in wider confidence intervals because they require a larger margin of error to ensure a higher probability of capturing the true population parameter.
- Explanation: Increasing the confidence level requires a larger critical value, which increases the margin of error and widens the confidence interval.
- Example: A 99% confidence interval will be wider than a 95% confidence interval for the same data.
5.3 Variability In The Data
Higher variability in the data (as measured by the standard deviation) leads to wider confidence intervals because it increases the uncertainty in the estimate.
- Explanation: As the standard deviation increases, the standard error also increases, which widens the confidence interval.
- Example: A dataset with a standard deviation of 20 will produce a wider confidence interval than a dataset with a standard deviation of 10, assuming all other factors are equal.
5.4 Population Size
In some cases, especially when sampling without replacement from a finite population, the population size can affect the width of the confidence interval. However, this effect is typically negligible when the sample size is small relative to the population size.
- Explanation: When the sample size is a large proportion of the population size, a finite population correction factor is applied, which reduces the standard error and narrows the confidence interval.
- Example: If you are sampling 500 students from a school of 1000 students, the population size will have a noticeable effect on the width of the confidence interval. However, if you are sampling 500 people from a city of 1 million, the effect will be negligible.
6. Practical Examples Of Confidence Interval Comparison
To illustrate the concepts, consider the following practical examples of comparing confidence intervals in various fields.
6.1 Healthcare: Comparing Treatment Effectiveness
In healthcare, confidence intervals are often used to compare the effectiveness of different treatments.
- Scenario: A clinical trial compares a new drug to a standard treatment for reducing blood pressure. The mean reduction in systolic blood pressure is 15 mmHg with a 95% confidence interval of [12, 18] for the new drug, and 10 mmHg with a 95% confidence interval of [8, 12] for the standard treatment.
- Analysis: Since the confidence intervals do not overlap, and the entire interval for the new drug is above the interval for the standard treatment, there is strong evidence that the new drug is more effective in reducing blood pressure.
6.2 Marketing: Comparing Customer Satisfaction
In marketing, confidence intervals can be used to compare customer satisfaction levels for different products or services.
- Scenario: A company surveys customers about their satisfaction with two different products. The mean satisfaction score (on a scale of 1 to 10) is 7.5 with a 95% confidence interval of [7.0, 8.0] for Product A, and 8.2 with a 95% confidence interval of [7.8, 8.6] for Product B.
- Analysis: The confidence intervals overlap, but the entire interval for Product B is generally higher than that of Product A. This suggests that Product B might have slightly higher customer satisfaction, but the difference may not be statistically significant without further analysis.
6.3 Education: Comparing Student Performance
In education, confidence intervals are used to compare student performance across different schools or teaching methods.
- Scenario: A school district compares the mean test scores of students in two different schools. School A has a mean score of 78 with a 95% confidence interval of [75, 81], and School B has a mean score of 82 with a 95% confidence interval of [79, 85].
- Analysis: The confidence intervals do not overlap, suggesting that there is a statistically significant difference in the mean test scores between the two schools. School B appears to have higher student performance on average.
6.4 Environmental Science: Monitoring Pollution Levels
In environmental science, confidence intervals are used to monitor changes in pollution levels over time or compare pollution levels between different locations.
- Scenario: An environmental agency monitors air quality at two different locations. Location X has a mean pollution level of 45 ppm with a 95% confidence interval of [42, 48], and Location Y has a mean pollution level of 50 ppm with a 95% confidence interval of [47, 53].
- Analysis: The confidence intervals overlap, suggesting that the difference in pollution levels between the two locations may not be statistically significant. However, further analysis might be needed to confirm this, especially if there are concerns about the potential health impacts of even small differences in pollution levels.
7. Advanced Considerations In Confidence Interval Comparison
Beyond the basics, several advanced considerations can enhance the accuracy and interpretation of confidence interval comparisons.
7.1 Bonferroni Correction For Multiple Comparisons
When comparing multiple confidence intervals, the risk of making a Type I error (false positive) increases. The Bonferroni correction is a method to adjust the significance level to account for multiple comparisons.
- Explanation: The Bonferroni correction divides the desired alpha level (e.g., 0.05) by the number of comparisons being made. This reduces the risk of falsely concluding that there is a significant difference.
- Example: If you are comparing the means of 5 different groups, you would divide 0.05 by 5, resulting in a new alpha level of 0.01. This means that a p-value would need to be less than 0.01 to be considered statistically significant.
7.2 Bayesian Confidence Intervals (Credible Intervals)
Bayesian confidence intervals, also known as credible intervals, provide a different approach to estimating population parameters. They are based on Bayesian statistics, which incorporate prior knowledge or beliefs into the analysis.
- Explanation: Bayesian credible intervals represent the range of values in which the parameter is believed to lie with a certain probability, given the observed data and prior beliefs.
- Example: A Bayesian analysis might incorporate prior knowledge about the effectiveness of a drug when estimating its effect on a particular condition.
7.3 Non-Parametric Confidence Intervals
Non-parametric confidence intervals are used when the data do not meet the assumptions of parametric tests (e.g., normality). These methods do not rely on specific distributional assumptions and are therefore more robust.
- Explanation: Non-parametric methods, such as bootstrapping, can be used to construct confidence intervals for medians or other non-parametric measures.
- Example: If you have data on income levels, which are often not normally distributed, you might use a non-parametric method to construct a confidence interval for the median income.
7.4 Confidence Intervals For Regression Coefficients
In regression analysis, confidence intervals are used to estimate the uncertainty in the estimated regression coefficients. These intervals provide a range of plausible values for the true effect of the predictor variables on the outcome variable.
- Explanation: The confidence interval for a regression coefficient indicates the range in which the true coefficient is likely to fall, given the data.
- Example: If you are analyzing the relationship between education level and income, the confidence interval for the regression coefficient associated with education level would indicate the range of plausible values for the effect of each additional year of education on income.
8. Real-World Case Studies
Examining real-world case studies provides a deeper understanding of how confidence interval comparisons are applied in practice.
8.1 Case Study 1: Comparing Marketing Campaign Effectiveness
- Background: A marketing company runs two different advertising campaigns to promote a new product. They want to determine which campaign is more effective in increasing sales.
- Data: After one month, Campaign A resulted in an average sales increase of 15% with a 95% confidence interval of [12%, 18%], and Campaign B resulted in an average sales increase of 10% with a 95% confidence interval of [8%, 12%].
- Analysis: The confidence intervals do not overlap, suggesting that Campaign A is significantly more effective than Campaign B in increasing sales. The marketing company can confidently conclude that Campaign A is the better choice for promoting the product.
8.2 Case Study 2: Evaluating Educational Interventions
- Background: A school district implements a new reading program in one group of schools and compares the results to a control group of schools that did not receive the intervention.
- Data: At the end of the school year, the intervention group shows an average improvement in reading scores of 8 points with a 95% confidence interval of [6, 10], while the control group shows an average improvement of 3 points with a 95% confidence interval of [1, 5].
- Analysis: The confidence intervals do not overlap, indicating that the new reading program is significantly more effective in improving reading scores compared to the standard curriculum.
8.3 Case Study 3: Assessing Medical Device Performance
- Background: A medical device company is testing a new heart monitor. They compare its performance to an existing monitor in terms of accuracy in detecting heart rate abnormalities.
- Data: The new monitor has an average accuracy rate of 98% with a 95% confidence interval of [96%, 100%], while the existing monitor has an average accuracy rate of 95% with a 95% confidence interval of [93%, 97%].
- Analysis: The confidence intervals overlap, but the lower bound of the new monitor’s interval is higher than the lower bound of the existing monitor’s interval. This suggests that the new monitor may be more accurate, but further analysis and larger sample sizes might be needed to confirm this.
8.4 Case Study 4: Analyzing Customer Satisfaction In Retail
- Background: A retail chain wants to compare customer satisfaction scores between two of its store locations to identify areas for improvement.
- Data: Store A has an average customer satisfaction score of 4.2 out of 5 with a 95% confidence interval of [4.0, 4.4], while Store B has an average customer satisfaction score of 3.9 out of 5 with a 95% confidence interval of [3.7, 4.1].
- Analysis: The confidence intervals overlap, indicating that the difference in customer satisfaction scores between the two stores may not be statistically significant. The retail chain should investigate other factors, such as specific customer service issues or product availability, to identify areas for improvement in both stores.
9. Tools And Resources For Confidence Interval Comparison
Several tools and resources can assist in calculating and comparing confidence intervals, making the process more efficient and accurate.
9.1 Statistical Software Packages (SPSS, R, SAS)
Statistical software packages like SPSS, R, and SAS provide functions for calculating and comparing confidence intervals.
- Description: These packages offer a wide range of statistical tools, including functions for calculating confidence intervals for means, proportions, and regression coefficients.
- Benefits: They provide accurate calculations and allow for complex analyses, such as adjusting for multiple comparisons or conducting non-parametric tests.
9.2 Online Confidence Interval Calculators
Online confidence interval calculators provide a quick and easy way to calculate confidence intervals for simple scenarios.
- Description: These calculators typically require the user to input the sample size, sample mean, and standard deviation, and they will calculate the confidence interval.
- Benefits: They are convenient and accessible, making them useful for quick calculations and basic analyses.
9.3 Spreadsheets (Excel, Google Sheets)
Spreadsheets like Excel and Google Sheets can be used to calculate confidence intervals, although they may require more manual calculations.
- Description: These tools can perform basic statistical calculations, such as calculating the sample mean and standard deviation, and can be used to calculate the margin of error and confidence interval using formulas.
- Benefits: They are widely available and easy to use, making them a good option for simple analyses and data visualization.
9.4 Educational Resources And Tutorials
Numerous educational resources and tutorials are available online to help users understand how to calculate and compare confidence intervals.
- Description: These resources include textbooks, online courses, and tutorials that provide step-by-step instructions and examples for calculating and interpreting confidence intervals.
- Benefits: They provide a comprehensive understanding of the concepts and methods, enabling users to perform accurate and meaningful analyses.
10. Conclusion: Making Informed Decisions With Confidence Interval Comparison
Comparing confidence intervals is a valuable technique for assessing statistical significance and making informed decisions based on data analysis. By understanding the principles, techniques, and factors that affect confidence intervals, you can draw accurate conclusions and avoid common mistakes.
10.1 Recap Of Key Points
- Confidence intervals provide a range of plausible values for an unknown population parameter.
- Comparing confidence intervals involves assessing whether the ranges overlap and evaluating the practical significance of any observed differences.
- Non-overlapping intervals suggest a statistically significant difference, while overlapping intervals indicate the difference may not be significant.
- Factors such as sample size, confidence level, and variability in the data affect the width of confidence intervals.
- Tools and resources such as statistical software packages, online calculators, and educational materials can assist in calculating and comparing confidence intervals.
10.2 Final Thoughts On The Importance Of Statistical Rigor
Statistical rigor is essential for ensuring the validity and reliability of research findings. By using confidence intervals correctly and considering all relevant factors, you can make more informed decisions and draw more accurate conclusions from data.
10.3 Encouragement To Explore Further At COMPARE.EDU.VN
We encourage you to explore further resources at COMPARE.EDU.VN to enhance your understanding of confidence interval comparison and other statistical techniques. Our website provides a wealth of information and tools to help you make informed decisions based on data analysis.
10.4 Call To Action
Ready to make smarter comparisons? Visit COMPARE.EDU.VN today to discover comprehensive comparisons and insightful data analysis that will empower you to make the best choices. Whether you’re comparing products, services, or ideas, COMPARE.EDU.VN offers the resources you need to succeed. For more information, contact us at:
- Address: 333 Comparison Plaza, Choice City, CA 90210, United States
- WhatsApp: +1 (626) 555-9090
- Website: compare.edu.vn
FAQ: Understanding Confidence Interval Comparison
1. What is the primary goal of comparing confidence intervals?
The primary goal is to determine if there are statistically significant differences between the means or proportions of two or more populations. This involves assessing whether the confidence intervals overlap and evaluating the practical significance of any observed differences.
2. How does the overlap of confidence intervals affect the interpretation of results?
Non-overlapping confidence intervals generally suggest a statistically significant difference between the groups being compared. Overlapping intervals indicate that the difference may not be statistically significant.
3. What factors can influence the width of a confidence interval?
The width of a confidence interval is influenced by several factors, including sample size, confidence level, and variability in the data. Larger sample sizes and lower variability lead to narrower intervals, while higher confidence levels result in wider intervals.
4. Can you use confidence intervals to compare more than two groups?
Yes, confidence intervals can be used to compare more than two groups. However, it is important to adjust for multiple comparisons to avoid an increased risk of Type I errors (false positives). Methods such as the Bonferroni correction can be used for this purpose.
5. What is the Bonferroni correction, and when should it be used?
The Bonferroni correction is a method to adjust the significance level when making multiple comparisons. It divides the desired alpha level (e.g., 0.05) by the number of comparisons being made. This correction should be used whenever you are comparing multiple confidence intervals to reduce the risk of falsely concluding that there is a significant difference.
6. What is the difference between statistical significance and practical significance?
Statistical significance refers to whether the observed difference between groups is likely to be due to chance. Practical significance refers to whether the difference is meaningful in a real-world context. A statistically significant difference may not always be practically important, and vice versa.
7. How do you calculate the difference between means and its confidence interval?
To calculate the difference between means, subtract the mean of one group from the mean of the other group. The confidence interval for this difference can be calculated using the standard error of the difference and a critical value from the t-distribution or z-distribution, depending on the sample size and whether the population standard deviations are known.
8. What are Bayesian confidence intervals, and how do they differ from traditional confidence intervals?
Bayesian confidence intervals, also known as credible intervals, are based on Bayesian statistics and incorporate prior knowledge or beliefs into the analysis. Unlike traditional confidence intervals, which are based solely on sample data, credible intervals represent the range of values in which the parameter is believed to lie with a certain probability, given the observed data and prior beliefs.
9. When should you use non-parametric confidence intervals?
Non-parametric confidence intervals should be used when the data do not meet the assumptions of parametric tests (e.g., normality). These methods do not rely on specific distributional assumptions and are therefore more robust.
10. Where can I find tools and resources for calculating and comparing confidence intervals?
Tools and resources for calculating and comparing confidence intervals include statistical software packages (SPSS, R, SAS), online confidence interval calculators, spreadsheets (Excel, Google Sheets), and educational resources and tutorials available online. These tools can help you perform accurate and meaningful analyses.