What Is the Difference Between Rope Tension Compared to Weight?

Tension in a rope and weight are both forces, but they act in different ways. Rope tension is a pulling force transmitted through a rope or cable, while weight is the force of gravity acting on an object’s mass. This article from COMPARE.EDU.VN delves into the nuances, exploring how these forces interact and influence various scenarios. Understanding these differences is crucial in fields like physics, engineering, and even everyday activities like lifting objects or securing loads. We will also compare and discuss related topics such as Free-body diagrams, Newton’s laws of motion and force vectors.

1. Defining Tension and Weight

To understand how “Can Rope Tension Compared To Weight,” it’s essential to define each term clearly. Tension and weight are both forces, but they originate from different sources and act in different directions.

1.1. What is Tension?

Tension is the pulling force transmitted axially through a rope, cable, string, or similar object, or by each end of a rod, truss member, or similar three-dimensional object. Tension is often described as the force that is transmitted through a string, rope, cable or wire when it is pulled tight by forces acting from opposite ends. The tension force is directed along the length of the wire and pulls equally on the objects on the opposite ends of the wire.

• Definition: Tension is the force transmitted through a rope, string, cable, or wire when pulled tight by forces acting from opposite ends.
• Direction: Tension always acts along the direction of the rope or cable, pulling equally on the objects attached to its ends.
• Units: Measured in Newtons (N) in the metric system or pounds (lbs) in the imperial system.
• Examples:
  • A rope pulling a box across the floor.
  • A cable suspending an elevator.
  • A string holding a kite in the air.

1.2. What is Weight?

Weight is the force exerted on an object due to gravity. It is directly proportional to the object’s mass and the acceleration due to gravity.

• Definition: Weight is the force exerted on an object due to gravity.
• Direction: Weight always acts vertically downward, towards the center of the Earth (or the center of the celestial body exerting the gravitational pull).
• Units: Measured in Newtons (N) in the metric system or pounds (lbs) in the imperial system, the same as force.
• Formula: Weight (W) = mass (m) × acceleration due to gravity (g), where g is approximately 9.81 m/s² on Earth.
• Examples:
  • A book resting on a table.
  • A person standing on the ground.
  • An apple falling from a tree.

1.3 Tension Force

The tension force is a pulling force that is transmitted through a rope, cable, string, or similar object when it is pulled tight by forces acting from opposite ends. It is always directed along the length of the rope or cable and pulls equally on the objects on the opposite ends.

The magnitude of the tension force can vary depending on the forces acting on the rope or cable. For example, if a rope is used to lift a heavy object, the tension in the rope will be equal to the weight of the object. However, if the rope is also being pulled horizontally, the tension in the rope will be greater than the weight of the object.

The tension force is an important concept in physics and engineering. It is used to analyze the forces acting on objects in a variety of situations, such as when lifting objects, towing vehicles, and suspending bridges.

1.4. Weight Force

The weight force is the force exerted on an object due to gravity. It is directly proportional to the object’s mass and the acceleration due to gravity. The formula for weight is:

Weight = mass × acceleration due to gravity

On Earth, the acceleration due to gravity is approximately 9.8 meters per second squared. So, the weight of an object on Earth is equal to its mass multiplied by 9.8 meters per second squared.

For example, a 10-kilogram object on Earth has a weight of 98 Newtons.

The weight force is always directed downwards, towards the center of the Earth. It is an important concept in physics and engineering. It is used to analyze the forces acting on objects in a variety of situations, such as when calculating the stability of structures and the motion of projectiles.

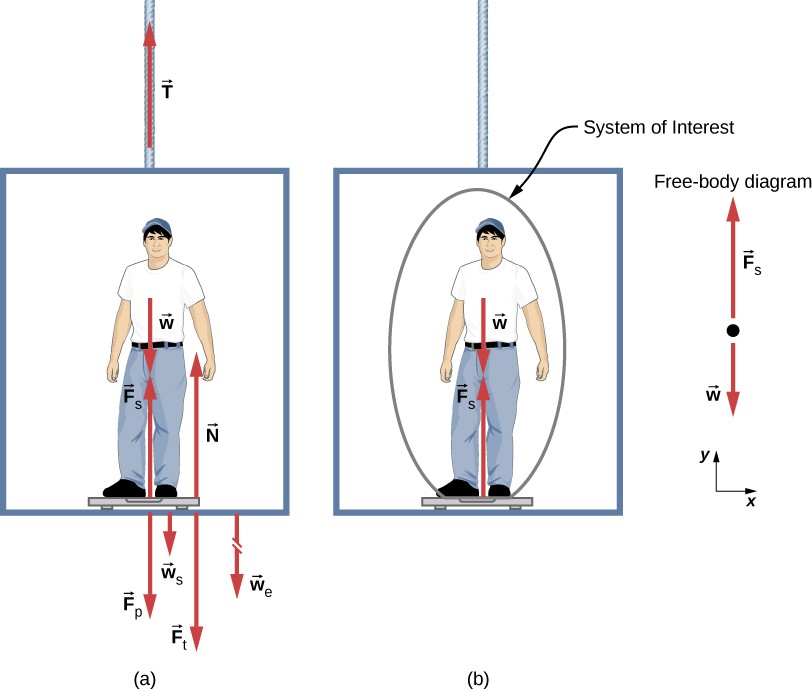Forces acting on a person in an elevator, including tension in the cable and the person's weight.

2. Key Differences Between Tension and Weight

Understanding “can rope tension compared to weight” requires identifying their differences, here’s a comparison in tabular form:

Feature	Tension	Weight
Definition	Pulling force transmitted through a rope, cable, or similar object.	Force exerted on an object due to gravity.
Direction	Along the direction of the rope or cable.	Vertically downward, towards the center of the Earth.
Source	External forces pulling on the rope or cable.	Gravitational attraction between the object and the Earth (or other celestial body).
Dependence	Depends on the applied forces and the properties of the rope/cable.	Depends on the object’s mass and the acceleration due to gravity.
Formula	Varies depending on the situation; often calculated using free-body diagrams and Newton’s laws.	W = m × g (Weight = mass × acceleration due to gravity).
Object Contact	Requires direct contact via a rope or cable.	Acts on the object whether it’s in contact with anything or not.

3. How Tension and Weight Interact

Tension and weight often interact in various physical scenarios. Understanding these interactions is vital in solving physics problems and designing engineering structures.

3.1. Static Equilibrium

In static equilibrium, an object is at rest, and the net force acting on it is zero. This means that all forces, including tension and weight, must balance each other.

• Example: A lamp suspended from the ceiling by a rope.
  • The weight of the lamp acts downward.
  • The tension in the rope acts upward.
  • In equilibrium, the tension in the rope equals the weight of the lamp.

3.2. Dynamic Equilibrium

Dynamic equilibrium occurs when an object moves at a constant velocity, meaning there is no acceleration. Again, the net force acting on the object must be zero.

• Example: An elevator moving upward at a constant speed.
  • The weight of the elevator acts downward.
  • The tension in the cable acts upward.
  • In dynamic equilibrium, the tension in the cable equals the weight of the elevator.

3.3. Accelerating Systems

When an object is accelerating, the net force acting on it is not zero. According to Newton’s second law (F = ma), the net force is equal to the mass of the object times its acceleration.

• Example: An elevator accelerating upward.
  • The weight of the elevator acts downward.
  • The tension in the cable acts upward.
  • The tension in the cable must be greater than the weight of the elevator to produce the upward acceleration.
  • Mathematically: T – W = ma, where T is tension, W is weight, m is mass, and a is acceleration.

4. Factors Affecting Tension in a Rope

Several factors can affect the tension in a rope, including the weight of the object being supported, any acceleration of the system, and the angle at which the rope is pulled.

4.1. Weight of the Object

The weight of the object being supported by the rope directly affects the tension in the rope. The heavier the object, the greater the tension required to support it.

• Example: Lifting a heavy box versus lifting a light box. The rope will experience more tension when lifting the heavy box.

4.2. Acceleration of the System

If the system is accelerating, the tension in the rope will be different from the weight of the object. As seen in the elevator example, upward acceleration increases tension, while downward acceleration decreases it.

• Example: A person in an accelerating elevator. The tension in the elevator cable changes depending on whether the elevator is accelerating upward or downward.

4.3. Angle of the Rope

The angle at which the rope is pulled also affects the tension. When a rope is pulled at an angle, only a component of the tension force acts to balance the weight.

• Example: A tug-of-war game. The angle at which each team pulls the rope affects the tension in the rope. A smaller angle (closer to horizontal) requires more tension to achieve the same effect.

5. Calculating Tension in Different Scenarios

Calculating tension involves applying Newton’s laws of motion and understanding the forces acting on the system.

5.1. Simple Vertical Suspension

When an object is suspended vertically by a rope, the tension in the rope is equal to the weight of the object, assuming the system is in equilibrium (not accelerating).

• Formula: T = W = m × g
• Example: A mass of 5 kg hanging from a rope.
  • Weight (W) = 5 kg × 9.81 m/s² = 49.05 N
  • Tension (T) = 49.05 N

5.2. Inclined Plane

On an inclined plane, the weight of the object is resolved into components parallel and perpendicular to the plane. The tension in the rope (if the object is being held in place or pulled up the plane) will balance the component of the weight parallel to the plane.

• Formula: T = m × g × sin(θ), where θ is the angle of inclination.
• Example: A block of mass 10 kg on a 30-degree incline, held by a rope.
  • T = 10 kg × 9.81 m/s² × sin(30°)
  • T = 10 kg × 9.81 m/s² × 0.5 = 49.05 N

5.3. Horizontal Pull

When an object is pulled horizontally by a rope, and there is friction, the tension in the rope must overcome both the frictional force and any component of weight acting against the motion.

• Formula: T = f + m × a, where f is the frictional force, m is mass, and a is acceleration.
• Example: Pulling a 20 kg box horizontally with a coefficient of friction of 0.2 and an acceleration of 1 m/s².
  • Frictional force (f) = μ × N = 0.2 × (20 kg × 9.81 m/s²) = 39.24 N
  • Tension (T) = 39.24 N + (20 kg × 1 m/s²) = 59.24 N

6. Real-World Applications

The concepts of tension and weight are fundamental to many real-world applications, from engineering design to everyday activities.

6.1. Engineering and Construction

In engineering and construction, understanding tension and weight is crucial for designing safe and stable structures.

• Bridges: Suspension bridges rely on cables to support the weight of the bridge deck and traffic. Engineers must calculate the tension in these cables to ensure they can withstand the load.
• Buildings: The weight of the building materials and the loads they support create tension in the structural members, such as beams and columns.
• Cranes: Cranes use cables and pulleys to lift heavy objects. The tension in the cables must be carefully calculated to prevent them from breaking.

6.2. Sports and Recreation

Tension and weight also play a role in various sports and recreational activities.

• Rock Climbing: Climbers use ropes to support their weight and manage tension while ascending rock faces.
• Sailing: The tension in the sails and rigging of a sailboat is essential for harnessing the wind and propelling the boat forward.
• Weightlifting: Weightlifters must overcome the weight of the barbell by applying an upward force, creating tension in their muscles and supporting structures.

6.3. Everyday Life

Even in everyday life, we encounter situations where tension and weight are important.

• Hanging Clothes: When you hang clothes on a clothesline, the tension in the line supports the weight of the clothes.
• Using an Elevator: The tension in the elevator cable supports the weight of the elevator car and its occupants.
• Carrying Groceries: The tension in the handles of grocery bags supports the weight of the items inside.

7. Common Misconceptions

There are several common misconceptions about tension and weight that can lead to confusion.

7.1. Tension is Only in Ropes

While tension is commonly associated with ropes, it can also exist in other objects, such as cables, wires, and even solid materials under tensile stress.

7.2. Weight is the Same as Mass

Weight and mass are related but distinct concepts. Mass is a measure of the amount of matter in an object, while weight is the force exerted on that mass due to gravity. Weight can change depending on the gravitational field, while mass remains constant.

7.3. Tension is Always Equal to Weight

Tension is only equal to weight in specific situations, such as when an object is suspended vertically and at rest. In other scenarios, such as accelerating systems or angled ropes, tension and weight are not equal.

8. Advanced Concepts Related to Tension and Weight

To gain a deeper understanding of tension and weight, it is helpful to explore some advanced concepts.

8.1. Free-Body Diagrams

A free-body diagram is a visual tool used to analyze the forces acting on an object. It involves drawing a diagram of the object and representing each force acting on it as a vector. This helps in applying Newton’s laws of motion to solve for unknown forces, such as tension.

• How to create a free-body diagram:
  1. Identify the object of interest.
  2. Draw a point representing the object.
  3. Draw vectors representing each force acting on the object, including tension, weight, normal force, friction, etc.
  4. Label each force vector with its magnitude and direction.

8.2. Newton’s Laws of Motion

Newton’s laws of motion are fundamental principles that govern the behavior of objects under the influence of forces.

• Newton’s First Law (Law of Inertia): An object at rest stays at rest, and an object in motion stays in motion with the same speed and in the same direction unless acted upon by a force.
• Newton’s Second Law: The acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass (F = ma).
• Newton’s Third Law: For every action, there is an equal and opposite reaction.

8.3. Vector Components

Forces are vector quantities, meaning they have both magnitude and direction. When dealing with forces at angles, it is often necessary to resolve them into horizontal and vertical components.

• How to resolve a force into components:
  • Use trigonometry to find the horizontal (x) and vertical (y) components of the force.
  • Fx = F × cos(θ), where F is the magnitude of the force and θ is the angle relative to the horizontal.
  • Fy = F × sin(θ), where F is the magnitude of the force and θ is the angle relative to the horizontal.

9. Practical Examples and Exercises

To reinforce your understanding of tension and weight, let’s consider some practical examples and exercises.

9.1. Example Problem: Hanging Sign

A sign weighing 50 N is hung from a ceiling by two ropes that make an angle of 30 degrees with the horizontal. What is the tension in each rope?

• Solution:
  1. Draw a free-body diagram of the sign.
  2. Resolve the tension in each rope into horizontal and vertical components.
  3. Apply equilibrium conditions:
     • ∑Fx = 0 (horizontal forces balance)
     • ∑Fy = 0 (vertical forces balance)
  4. Solve for the tension in each rope.
  5. Tension in each rope ≈ 28.87 N

9.2. Exercise: Block on an Inclined Plane

A 10 kg block rests on an inclined plane with an angle of 45 degrees. A rope is attached to the block and pulled parallel to the incline to prevent the block from sliding down. What is the tension in the rope?

• Steps to solve:
  1. Draw a free-body diagram of the block.
  2. Resolve the weight of the block into components parallel and perpendicular to the incline.
  3. Set the tension in the rope equal to the component of weight parallel to the incline.
  4. Calculate the tension.

9.3. Example Problem: Elevator Acceleration

A 500 kg elevator is accelerating upwards at a rate of 2 m/s². What is the tension in the cable supporting the elevator?

• Solution:

1. Identify the forces:
   • Weight of the elevator (W) = m g = 500 kg 9.8 m/s² = 4900 N (downwards)
   • Tension in the cable (T) – upwards
2. Apply Newton’s Second Law:
   • F_net = m * a
   • T – W = m * a
   • T – 4900 N = 500 kg * 2 m/s²
3. Solve for Tension (T):
   • T = 500 kg * 2 m/s² + 4900 N
   • T = 1000 N + 4900 N
   • T = 5900 N

Therefore, the tension in the cable supporting the elevator is 5900 N.

9.4. Exercise: Two Blocks Connected by a Rope

Two blocks are connected by a rope over a pulley. Block A has a mass of 5 kg and rests on a horizontal surface with a coefficient of kinetic friction of 0.2. Block B has a mass of 3 kg and hangs vertically. Determine the tension in the rope and the acceleration of the system.

• Steps to solve:

1. Draw free-body diagrams for both blocks.
2. Identify all forces acting on each block.
3. Apply Newton’s Second Law to each block.
4. Solve the system of equations to find the tension and acceleration.

By working through these examples and exercises, you can develop a better understanding of how tension and weight interact in various situations.

10. Conclusion: Mastering the Concepts of Tension and Weight

Understanding “can rope tension compared to weight” is fundamental to comprehending mechanics and force interactions. Tension is a pulling force transmitted through ropes or cables, while weight is the force of gravity acting on an object’s mass. These forces interact in various scenarios, from static equilibrium to accelerating systems.

By grasping these concepts, you can better analyze and solve problems related to engineering, physics, and everyday life. COMPARE.EDU.VN provides comprehensive resources and comparisons to further enhance your understanding and decision-making in various fields.

Are you still struggling to compare and analyze different scenarios involving tension and weight? Do you need a clearer, more objective comparison to make informed decisions? Visit COMPARE.EDU.VN today! Our detailed comparisons will help you understand the nuances and make confident choices.

Contact us at:

Address: 333 Comparison Plaza, Choice City, CA 90210, United States

WhatsApp: +1 (626) 555-9090

Website: compare.edu.vn

FAQ: Frequently Asked Questions About Tension and Weight

1. Is tension a scalar or a vector quantity?

Tension is a vector quantity because it has both magnitude and direction. The direction of tension is always along the direction of the rope or cable.

2. Can tension be negative?

No, tension is always a pulling force and cannot be negative. However, in certain problem-solving contexts, you might assign a negative sign to tension if it acts in the opposite direction to your chosen positive direction.

3. How does friction affect tension in a rope?

Friction can increase the tension required in a rope, especially when pulling an object horizontally. The tension must overcome the frictional force to move the object.

4. What happens to the tension in a rope if it is cut?

If a rope is cut, the tension in the rope becomes zero. The two ends of the rope will no longer exert a pulling force on each other.

5. How does the length of a rope affect the tension?

The length of a rope does not directly affect the tension, assuming the weight and other forces acting on the rope remain constant.

6. Can tension exist in a rigid object?

Yes, tension can exist in a rigid object under tensile stress. Tensile stress is the force per unit area that causes the object to stretch.

7. How does acceleration affect tension in a cable?

Acceleration can significantly affect the tension in a cable. If an object is accelerating upwards, the tension in the cable will be greater than the weight of the object. If the object is accelerating downwards, the tension will be less than the weight.

8. What is the difference between tension and compression?

Tension is a pulling force that tends to stretch an object, while compression is a pushing force that tends to compress an object.

9. How do pulleys affect tension in a rope?

Pulleys can change the direction of the tension force and reduce the amount of force needed to lift an object. A system of pulleys can provide a mechanical advantage, allowing you to lift heavy objects with less effort.

10. Is the tension the same throughout a rope?

In an ideal rope (massless and frictionless), the tension is the same throughout the rope. However, in real-world scenarios, the tension can vary slightly due to the weight of the rope and friction.