A Ratio Comparing Two Quantities With Different Units, often referred to as a rate, expresses the relationship between these quantities. COMPARE.EDU.VN offers detailed comparisons to help you understand and apply this concept effectively in various scenarios. By exploring unit rates and unit prices, you can make informed decisions in everyday life. Enhance your decision-making with comprehensive comparative analyses and insightful ratio evaluations.
1. Understanding Ratios
1.1. Defining Ratios and Their Importance
A ratio is a comparison of two quantities using division. It can be expressed in several ways:
- With the word “to”: 3 to 4
- As a fraction: (frac{3}{4})
- With a colon: 3:4
Ratios are fundamental in mathematics and are widely used across various disciplines, from finance to physics. Understanding ratios helps in making proportional comparisons and informed decisions.
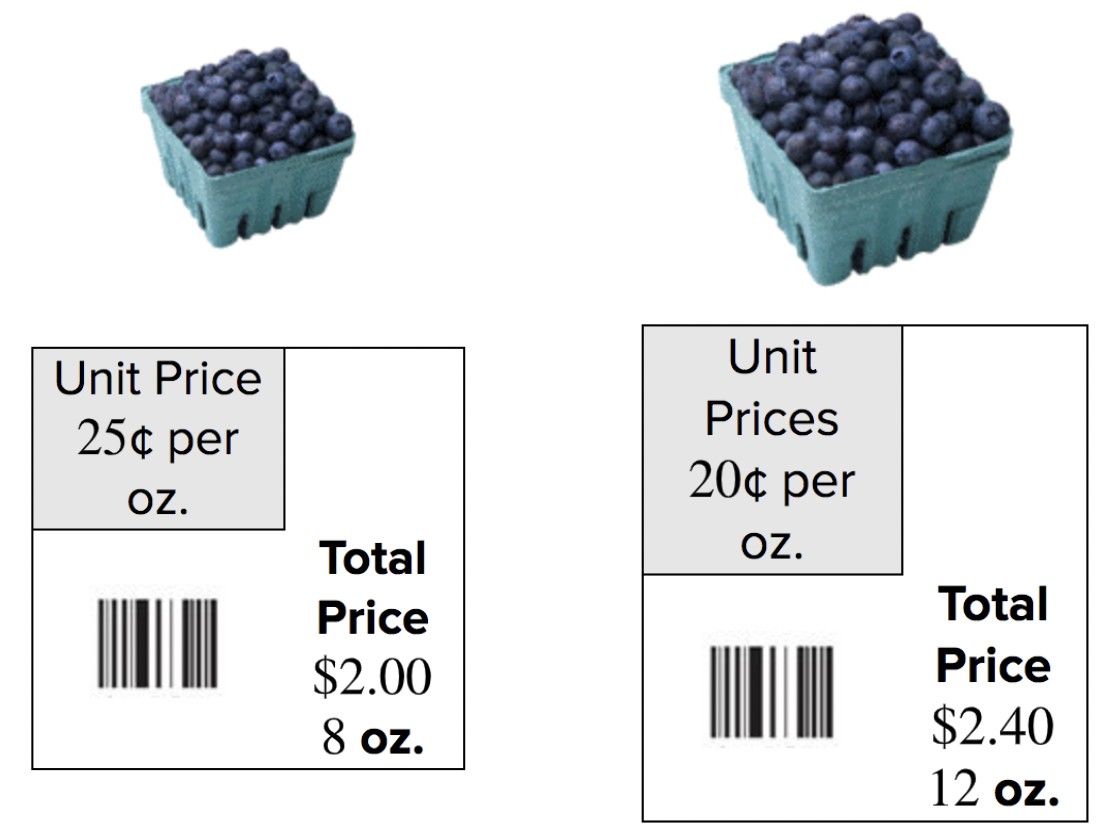ratio-example
Alt text: Two containers of blueberries with different prices and quantities, used to illustrate the concept of unit price.
1.2. Expressing Ratios in Simplest Form
A ratio is simplified when it is equivalent to a fraction that has been reduced to its lowest terms. Simplifying ratios makes it easier to understand and compare different relationships. For instance, the ratio 20:30 can be simplified to 2:3 by dividing both numbers by their greatest common divisor, which is 10.
1.3. Examples of Ratios in Everyday Life
Ratios are prevalent in everyday scenarios:
- Cooking: A recipe might call for a ratio of 1 part water to 2 parts rice.
- Mixing: Mixing paint might require a ratio of 1 part pigment to 5 parts base.
- Scaling: Adjusting a recipe from serving 4 people to serving 8 people requires understanding ratios.
- Sports: The ratio of wins to losses for a sports team.
Understanding these ratios helps in performing tasks accurately and efficiently.
2. Delving Into Rates
2.1. What is a Rate?
A rate is a special type of ratio that compares two quantities with different units of measure. Examples include:
- Speed: Miles per hour (mph) or kilometers per hour (km/h).
- Wages: Dollars per hour ($/hr).
- Prices: Dollars per gallon ($/gallon) or euros per liter (€/liter).
The word “per” is often used to indicate a rate, highlighting the relationship between two different units. For example, if a car travels 120 miles in 2 hours, the rate is 60 miles per hour.
2.2. How Rates Differ from Ratios
The key difference between rates and ratios lies in the units of measure:
- Ratios compare quantities with the same units. For example, the ratio of apples to oranges in a basket.
- Rates compare quantities with different units. For example, the cost of gasoline per gallon.
This distinction is crucial because rates provide a way to relate dissimilar quantities, offering insights into real-world phenomena like speed, cost, and efficiency.
2.3. Practical Examples of Rates
Rates are essential in various practical applications:
- Transportation: Calculating fuel efficiency (miles per gallon) for vehicles.
- Finance: Determining interest rates on loans or investments (percent per year).
- Healthcare: Measuring heart rate (beats per minute).
- Manufacturing: Assessing production rates (units per hour).
These examples underscore the importance of rates in understanding and managing different aspects of daily life and professional fields.
3. Unit Rates: A Closer Look
3.1. Definition of Unit Rate
A unit rate compares a quantity to one unit of measure. It simplifies comparisons by providing a standardized measure. The denominator of a unit rate is always one.
3.2. How to Calculate Unit Rates
To calculate a unit rate, divide both the numerator and the denominator of the rate by the denominator’s value. For example, if a store sells 5 apples for $2.50, the unit rate is calculated as follows:
(frac{$2.50}{5 text{ apples}} = frac{$2.50 div 5}{5 text{ apples} div 5} = frac{$0.50}{1 text{ apple}})
The unit rate is $0.50 per apple.
3.3. Real-World Applications of Unit Rates
Unit rates are used extensively in:
- Shopping: Comparing prices of different products to find the best deal.
- Travel: Calculating the time it takes to travel a certain distance at a constant speed.
- Cooking: Adjusting recipe quantities based on the number of servings.
- Sports: Determining a player’s scoring rate (points per game).
These applications illustrate how unit rates help in making informed decisions and optimizing performance.
4. The Significance of Unit Prices
4.1. Defining Unit Price
A unit price is a unit rate that expresses the price of something per single unit. It is used to compare the cost-effectiveness of different products.
4.2. Finding the Best Deals with Unit Prices
To find the best deal using unit prices, calculate the price per unit for each option and compare them. The option with the lowest unit price offers the best value.
For instance, consider two options for buying cereal:
- Option A: A 10-ounce box for $3.00
- Option B: A 15-ounce box for $4.20
Calculating the unit prices:
- Option A: (frac{$3.00}{10 text{ ounces}} = $0.30 text{ per ounce})
- Option B: (frac{$4.20}{15 text{ ounces}} = $0.28 text{ per ounce})
Option B has a lower unit price ($0.28 per ounce) and is therefore the better deal.
4.3. Examples of Unit Price in Shopping
Unit prices are commonly displayed in grocery stores to help consumers compare products:
- Canned Goods: Comparing the price per ounce of different brands of canned vegetables.
- Dairy Products: Determining the cost per gallon of milk.
- Cleaning Supplies: Assessing the price per load of laundry detergent.
- Snacks: Comparing the cost per ounce of different snack foods.
By using unit prices, shoppers can make more economical choices and maximize their purchasing power.
5. Step-by-Step Examples of Calculating Ratios and Rates
5.1. Example 1: Calculating the Ratio of Students to Teachers
A school has 1,200 students and 60 teachers. Calculate the ratio of students to teachers.
- Identify the Quantities: Number of students = 1,200, Number of teachers = 60
- Write the Ratio: (frac{1200 text{ students}}{60 text{ teachers}})
- Simplify the Ratio: (frac{1200 div 60}{60 div 60} = frac{20}{1})
The ratio of students to teachers is 20:1, meaning there are 20 students for every teacher.
5.2. Example 2: Determining the Rate of Travel
A car travels 360 miles in 6 hours. Calculate the rate of travel in miles per hour.
- Identify the Quantities: Distance = 360 miles, Time = 6 hours
- Write the Rate: (frac{360 text{ miles}}{6 text{ hours}})
- Simplify the Rate: (frac{360 div 6}{6 div 6} = frac{60 text{ miles}}{1 text{ hour}})
The rate of travel is 60 miles per hour.
5.3. Example 3: Calculating the Unit Price of Eggs
A dozen eggs costs $3.60. Calculate the unit price per egg.
- Identify the Quantities: Total cost = $3.60, Number of eggs = 12
- Write the Rate: (frac{$3.60}{12 text{ eggs}})
- Simplify the Rate: (frac{$3.60 div 12}{12 div 12} = frac{$0.30}{1 text{ egg}})
The unit price is $0.30 per egg.
6. Advanced Applications of Ratios and Rates
6.1. Using Ratios in Financial Analysis
In finance, ratios are used to analyze a company’s performance:
- Debt-to-Equity Ratio: Measures a company’s financial leverage.
- Profit Margin: Indicates how much profit a company makes for every dollar of revenue.
- Current Ratio: Assesses a company’s ability to pay short-term obligations.
These ratios provide insights into a company’s financial health and performance.
6.2. Rates in Scientific Measurements
Rates are fundamental in scientific measurements:
- Reaction Rates: In chemistry, the speed at which a chemical reaction occurs.
- Flow Rates: In physics, the volume of fluid that passes through a point per unit time.
- Growth Rates: In biology, the rate at which a population increases.
These rates are essential for understanding and predicting natural phenomena.
6.3. Ratios and Rates in Data Analysis
In data analysis, ratios and rates are used to:
- Conversion Rates: The percentage of website visitors who complete a desired action.
- Click-Through Rates: The percentage of people who click on a specific link.
- Error Rates: The percentage of errors in a dataset.
These metrics are crucial for evaluating performance and making data-driven decisions.
7. Common Mistakes to Avoid When Working with Ratios and Rates
7.1. Misunderstanding Units
A common mistake is failing to pay attention to the units of measure. Always ensure that the units are consistent when comparing ratios or rates.
7.2. Incorrect Simplification
Incorrectly simplifying ratios or rates can lead to inaccurate comparisons. Double-check your calculations to ensure the ratio or rate is in its simplest form.
7.3. Confusing Ratios and Rates
Remember that ratios compare quantities with the same units, while rates compare quantities with different units. Confusing the two can lead to misinterpretations.
8. Proven Methodologies for Mastering Ratios and Rates
8.1. Structured Learning Approaches
Follow a structured curriculum that systematically covers ratios and rates, including their definitions, properties, and applications. This approach ensures a solid foundation and progressive understanding.
8.2. Hands-On Practice with Real-World Scenarios
Engage in hands-on activities involving real-world scenarios to apply the concepts learned. This includes solving practical problems related to finance, shopping, cooking, and other relevant areas.
8.3. Utilizing Interactive Tools and Resources
Leverage interactive tools and resources, such as online calculators, simulations, and educational games, to enhance your understanding and skills in working with ratios and rates.
9. Maximizing the Benefits of Ratios and Rates in Decision-Making
9.1. Identifying Key Performance Indicators (KPIs)
Learn to identify and use relevant Key Performance Indicators (KPIs) that involve ratios and rates to track progress, measure performance, and make data-driven decisions in various domains.
9.2. Comparative Analysis Techniques
Develop skills in comparative analysis by comparing different options using ratios and rates. This enables informed decision-making when evaluating products, services, or strategies.
9.3. Risk Assessment and Mitigation Strategies
Apply ratios and rates to assess and mitigate risks in financial and operational contexts. This includes evaluating debt-to-equity ratios, profit margins, and other relevant metrics to make informed risk management decisions.
10. How to Use COMPARE.EDU.VN to Enhance Your Understanding
10.1. Accessing Detailed Comparison Articles
Visit COMPARE.EDU.VN to access detailed comparison articles that provide comprehensive analyses of various products, services, and ideas using ratios and rates.
10.2. Utilizing Interactive Comparison Tools
Take advantage of interactive comparison tools available on the website to compare different options based on your specific criteria and preferences, ensuring informed decision-making.
10.3. Engaging with Expert Reviews and Recommendations
Explore expert reviews and recommendations on COMPARE.EDU.VN to gain valuable insights and guidance from industry professionals, helping you make well-informed choices.
FAQ About Ratios and Rates
11.1. What is the difference between a ratio and a proportion?
A ratio compares two quantities, while a proportion is an equation stating that two ratios are equal.
11.2. How do you convert a ratio to a percentage?
To convert a ratio to a percentage, divide the first quantity by the second quantity and multiply by 100.
11.3. Can a ratio have more than two terms?
Yes, a ratio can have more than two terms. For example, a ratio of 1:2:3 compares three quantities.
11.4. What is a compound rate?
A compound rate is a rate that changes over time, often used in financial calculations like compound interest.
11.5. How are rates used in cooking?
Rates are used to adjust recipe quantities. For example, if a recipe calls for 2 cups of water per 1 cup of rice, the rate is 2:1.
11.6. What is the importance of unit price in budgeting?
Unit price helps in making informed purchasing decisions, ensuring you get the best value for your money.
11.7. How do you calculate the unit rate when the quantities are in different units?
Ensure both quantities are in the same unit before calculating the unit rate. Convert the units if necessary.
11.8. What is the role of rates in scientific experiments?
Rates help in measuring and analyzing changes over time, such as reaction rates or growth rates.
11.9. How can ratios and rates help in sports analysis?
Ratios and rates can be used to calculate player statistics, such as scoring rates or win-loss ratios, providing insights into performance.
11.10. What are some examples of rates in environmental science?
Examples include pollution rates (e.g., parts per million), deforestation rates (e.g., hectares per year), and species extinction rates.
12. Conclusion
Understanding ratios and rates, especially “a ratio comparing two quantities with different units,” is essential for making informed decisions in various aspects of life. Whether you’re comparing prices while shopping, analyzing financial data, or interpreting scientific measurements, these concepts provide valuable insights. For more detailed comparisons and expert advice, visit COMPARE.EDU.VN at 333 Comparison Plaza, Choice City, CA 90210, United States. Contact us via WhatsApp at +1 (626) 555-9090.
Are you struggling to make informed decisions due to the complexity of comparing different options? Do you find it challenging to objectively evaluate products, services, or ideas? Visit COMPARE.EDU.VN today to discover comprehensive comparisons and make confident choices. Our detailed analyses and user-friendly tools simplify the decision-making process, helping you find the best solutions for your needs. Don’t stay confused—explore compare.edu.vn now and make smarter decisions!
