A ratio is a ratio that compares two quantities, providing a way to understand their relative sizes. COMPARE.EDU.VN offers comprehensive comparisons to help you make informed decisions. Understanding ratios, proportional relationships and equivalent ratios is crucial in various fields from mathematics to everyday life. Explore different quantities and proportional reasoning with us.
1. Understanding the Essence of Ratios
Ratios play a fundamental role in mathematics and everyday life, offering a way to compare two quantities. Whether you’re comparing ingredients in a recipe or analyzing data sets, understanding ratios is essential.
1.1. Defining a Ratio: The Basics
A ratio is a ratio that compares two quantities, illustrating their relative sizes. It can be expressed in several ways, including fractions, decimals, and percentages, depending on the context and desired level of precision. Understanding this fundamental concept allows for insightful comparisons and informed decision-making. Ratios are used to express the size of a number in relation to another number.
 Sugar Cookie vs Chocolate Chip Cookies Ratio
Sugar Cookie vs Chocolate Chip Cookies Ratio
1.2. Different Ways to Express a Ratio
Ratios can be expressed in three primary ways:
- Fraction: (frac{a}{b}), where ‘a’ and ‘b’ are the quantities being compared.
- Colon: a : b, indicating the relationship between ‘a’ and ‘b’.
- Words: “a to b,” clearly stating the comparison between the two quantities.
1.3. Ratio vs. Rate: What’s the Difference?
While both ratios and rates compare quantities, rates specifically compare quantities with different units. For example, miles per hour is a rate, whereas the number of apples to oranges is a ratio.
2. Real-World Applications of Ratios
Ratios are not just theoretical concepts; they are practical tools used in various fields to make comparisons and inform decisions.
2.1. Ratios in Cooking: Getting the Recipe Right
In cooking, ratios are essential for maintaining the correct proportions of ingredients. For instance, a cake recipe might require a ratio of 2:1 for flour to sugar, ensuring the desired texture and taste.
2.2. Ratios in Business: Analyzing Financial Data
Businesses use ratios to analyze financial data, such as debt-to-equity ratios or current ratios, to assess their financial health and make strategic decisions.
2.3. Ratios in Science: Understanding Proportions
Scientists use ratios to understand proportions in experiments and observations. For example, the ratio of reactants in a chemical reaction or the ratio of species in an ecosystem.
3. Calculating and Simplifying Ratios
Calculating and simplifying ratios involves understanding how to reduce them to their simplest form, making comparisons easier.
3.1. How to Calculate a Ratio
To calculate a ratio, divide one quantity by the other and express the result as a fraction, decimal, or percentage. The choice depends on the context and the level of detail required.
3.2. Simplifying Ratios to Their Simplest Form
Simplifying a ratio involves finding the greatest common divisor (GCD) of the two quantities and dividing both by it. This reduces the ratio to its simplest form, making it easier to understand and compare.
3.3. Working with Ratios in Different Units
When working with ratios involving different units, it’s essential to convert them to the same unit before calculating the ratio. This ensures accurate comparisons and meaningful results.
4. Proportions: Understanding Equal Ratios
Proportions are statements of equality between two ratios. Understanding proportions is crucial for solving problems involving scaling, conversions, and other real-world scenarios.
4.1. What is a Proportion?
A proportion is an equation that states that two ratios are equal. It can be written as (frac{a}{b} = frac{c}{d}), indicating that the ratio of ‘a’ to ‘b’ is equal to the ratio of ‘c’ to ‘d’.
4.2. Solving Proportions Using Cross Multiplication
Cross multiplication is a technique used to solve proportions. It involves multiplying the numerator of one ratio by the denominator of the other and setting the products equal to each other.
4.3. Real-Life Examples of Proportions
Proportions are used in various real-life scenarios, such as scaling recipes, converting currencies, and calculating distances on maps.
5. Unit Rates: A Special Type of Ratio
Unit rates are a special type of ratio that compares a quantity to one unit of another quantity. They are commonly used to express prices, speeds, and other rates in a standardized way.
5.1. Defining Unit Rate
A unit rate expresses the amount of one item, such as a product, to a single measurement of another item. It can be used to describe things such as passengers per subway car.
( frac{300 text { miles}{div5 }}{5 text { hours}{div5 }}=frac{60 text { miles }}{1 text { hour }})
5.2. Calculating Unit Rates
To calculate a unit rate, divide the quantity by the number of units. For example, if a car travels 300 miles in 5 hours, the unit rate is 60 miles per hour.
5.3. Applications of Unit Rates in Everyday Life
Unit rates are used in everyday life to compare prices, calculate speeds, and make informed decisions. For example, when shopping for groceries, comparing unit prices can help you find the best deal.
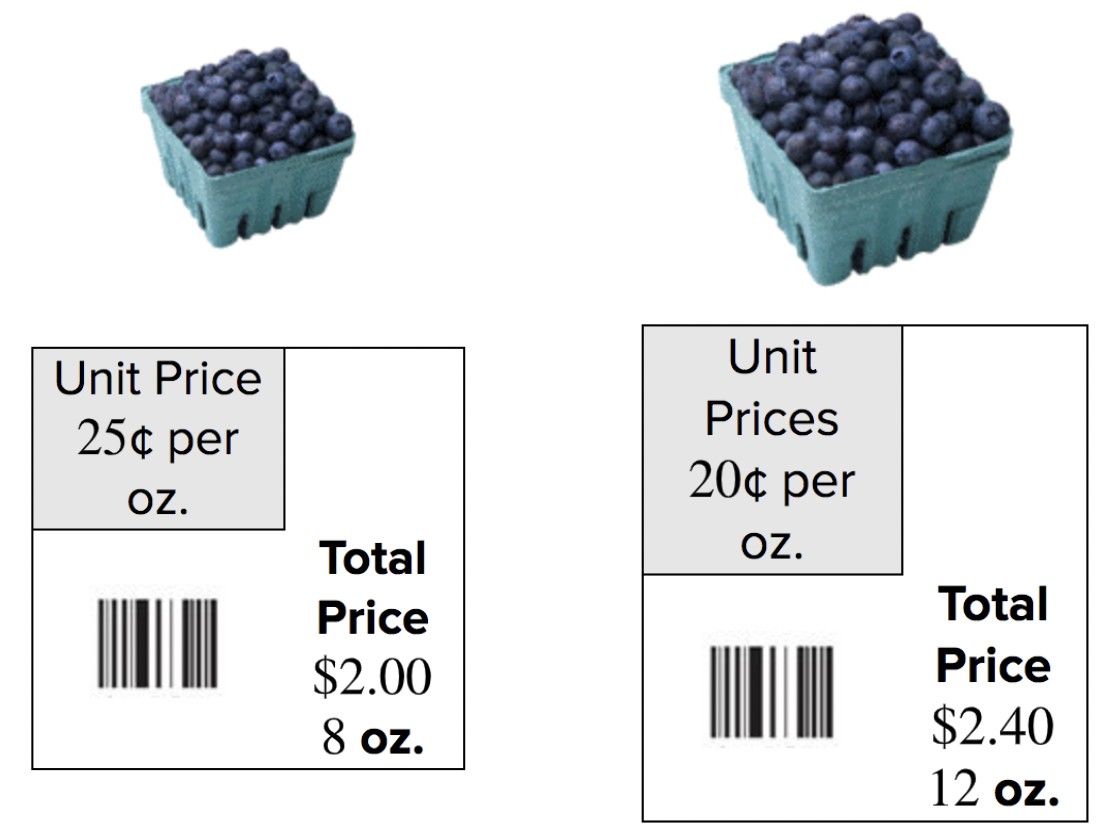
6. Unit Price: Making Smart Purchasing Decisions
Unit price is a specific type of unit rate that expresses the price of one unit of a product. It is a valuable tool for making smart purchasing decisions and comparing the value of different products.
6.1. Understanding Unit Price
A unit price is a unit rate that expresses the price of one unit of a product. It allows consumers to compare the cost of different products based on a standardized unit of measure.
6.2. Calculating Unit Price
To calculate the unit price, divide the total price by the number of units. For example, if a 10-pound bag of rice costs $10, the unit price is $1 per pound.
6.3. Comparing Products Using Unit Price
Unit price is a valuable tool for comparing products and making informed purchasing decisions. By comparing the unit prices of different products, consumers can determine which offers the best value for their money.
7. Common Mistakes to Avoid When Working with Ratios
Working with ratios can be tricky, and it’s easy to make mistakes if you’re not careful. Here are some common mistakes to avoid:
7.1. Mixing Up the Order of Quantities
When expressing a ratio, it’s essential to maintain the correct order of quantities. Reversing the order can lead to incorrect comparisons and misleading results.
7.2. Forgetting to Simplify Ratios
Failing to simplify ratios can make them difficult to compare and understand. Always simplify ratios to their simplest form to ensure clarity and accuracy.
7.3. Not Converting Units to the Same Measure
When working with ratios involving different units, it’s essential to convert them to the same unit before calculating the ratio. Failing to do so can lead to inaccurate comparisons and flawed conclusions.
8. Advanced Ratio Concepts
For those looking to deepen their understanding of ratios, here are some advanced concepts to explore:
8.1. Ratios and Scale Drawings
Scale drawings use ratios to represent objects or spaces at a different size. Understanding ratios is essential for interpreting and creating accurate scale drawings.
8.2. Ratios and Probability
Probability uses ratios to express the likelihood of an event occurring. Understanding ratios is crucial for calculating and interpreting probabilities accurately.
8.3. Ratios and Statistics
Statistics uses ratios to analyze data and draw conclusions. Understanding ratios is essential for interpreting statistical data and making informed decisions.
9. Practical Exercises to Improve Your Ratio Skills
To improve your ratio skills, here are some practical exercises to try:
9.1. Recipe Scaling
Scale a recipe up or down by adjusting the quantities of ingredients based on ratios. This exercise will help you understand how ratios are used in cooking and baking.
9.2. Financial Analysis
Analyze financial data using ratios to assess the financial health of a company. This exercise will help you understand how ratios are used in business and finance.
9.3. Map Reading
Use ratios to calculate distances on a map and plan a route. This exercise will help you understand how ratios are used in geography and navigation.
10. Leveraging COMPARE.EDU.VN for Informed Decisions
At COMPARE.EDU.VN, we understand the importance of informed decision-making. That’s why we provide comprehensive comparisons to help you make the right choices.
10.1. How COMPARE.EDU.VN Simplifies Comparisons
COMPARE.EDU.VN simplifies comparisons by providing detailed information on products, services, and ideas, making it easier for you to evaluate your options.
10.2. Using Ratios in Decision-Making with COMPARE.EDU.VN
You can use ratios to make informed decisions with COMPARE.EDU.VN. By comparing the ratios of different factors, you can identify the best option for your needs.
10.3. Success Stories: Real People, Smart Choices
Discover how others have used COMPARE.EDU.VN to make smart choices and achieve their goals. Our success stories demonstrate the value of informed decision-making.
11. Rates: Measuring Change and Speed
Rates are a fundamental concept in mathematics and physics, used to measure change and speed. They provide a way to quantify how one quantity changes in relation to another.
11.1. Definition and Importance of Rates
A rate is a ratio that compares two quantities with different units of measurement. Rates are commonly used to express speed, such as miles per hour, or prices, such as dollars per pound. Understanding rates is essential for solving problems involving motion, finance, and other real-world scenarios.
11.2. Calculating Average Speed
Average speed is calculated by dividing the total distance traveled by the total time taken. This calculation provides a measure of how quickly an object is moving on average over a given period.
11.3. Understanding Acceleration
Acceleration is the rate at which an object’s velocity changes over time. It is calculated by dividing the change in velocity by the time taken for the change to occur. Understanding acceleration is essential for analyzing the motion of objects in physics.
12. Proportional Relationships: Connecting Ratios and Rates
Proportional relationships exist when two quantities vary directly with each other, maintaining a constant ratio. Understanding proportional relationships is crucial for solving problems involving scaling, conversions, and other real-world scenarios.
12.1. Identifying Proportional Relationships
To identify proportional relationships, look for a constant ratio between two quantities. If the ratio remains constant as the quantities change, then a proportional relationship exists.
12.2. Solving Problems Involving Proportionality
Problems involving proportionality can be solved using cross multiplication or by setting up a proportion equation. These techniques allow you to find unknown quantities in proportional relationships.
12.3. Graphs of Proportional Relationships
The graph of a proportional relationship is a straight line that passes through the origin. The slope of the line represents the constant ratio between the two quantities.
13. Equivalent Ratios: Different Forms, Same Value
Equivalent ratios are ratios that have the same value, even though they may be expressed with different numbers. Understanding equivalent ratios is essential for simplifying ratios and making accurate comparisons.
13.1. Finding Equivalent Ratios
To find equivalent ratios, multiply or divide both quantities in the ratio by the same number. This will create a new ratio that has the same value as the original ratio.
13.2. Using Equivalent Ratios to Solve Problems
Equivalent ratios can be used to solve problems involving scaling, conversions, and other real-world scenarios. By setting up equivalent ratios, you can find unknown quantities and make accurate comparisons.
13.3. Simplifying Complex Ratios
Simplifying complex ratios involves finding equivalent ratios that have smaller, whole number quantities. This makes the ratio easier to understand and compare.
14. Scaling Recipes: Adjusting Ingredients Proportionally
Scaling recipes involves adjusting the quantities of ingredients proportionally to make a larger or smaller batch. Understanding ratios is essential for scaling recipes accurately and maintaining the desired taste and texture.
14.1. Determining the Scaling Factor
The scaling factor is the number by which you multiply or divide the original quantities to get the new quantities. It is calculated by dividing the desired quantity by the original quantity.
14.2. Adjusting Ingredient Quantities
To adjust ingredient quantities, multiply or divide each ingredient by the scaling factor. This will ensure that the proportions of ingredients remain the same, even as the batch size changes.
14.3. Tips for Successful Recipe Scaling
- Use accurate measurements to ensure precise scaling.
- Consider the impact of scaling on cooking times and temperatures.
- Adjust seasonings and spices to taste, as needed.
15. Financial Ratios: Analyzing Company Performance
Financial ratios are used to analyze a company’s financial performance and assess its financial health. Understanding financial ratios is essential for investors, lenders, and other stakeholders.
15.1. Key Financial Ratios
- Liquidity Ratios: Measure a company’s ability to meet its short-term obligations.
- Profitability Ratios: Measure a company’s ability to generate profits.
- Solvency Ratios: Measure a company’s ability to meet its long-term obligations.
15.2. Interpreting Financial Ratios
Interpreting financial ratios involves comparing them to industry averages and historical trends. This allows you to assess a company’s financial performance relative to its peers and over time.
15.3. Using Financial Ratios for Investment Decisions
Financial ratios can be used to make informed investment decisions. By analyzing a company’s financial ratios, you can assess its risk and potential return.
16. Ratios in Geometry: Understanding Shapes and Sizes
Ratios play a crucial role in geometry, helping us understand the relationships between shapes and sizes. From scaling figures to understanding trigonometric ratios, ratios are fundamental to geometric concepts.
16.1. Similar Figures
Similar figures are figures that have the same shape but different sizes. The corresponding sides of similar figures are proportional, meaning they have the same ratio.
16.2. Scaling Figures
Scaling figures involves changing their size while maintaining their shape. This is done by multiplying or dividing the dimensions of the figure by a scaling factor.
16.3. Trigonometric Ratios
Trigonometric ratios, such as sine, cosine, and tangent, are used to relate the angles and sides of right triangles. These ratios are essential for solving problems involving angles and distances.
17. Ratios in Statistics: Analyzing Data and Trends
Statistics uses ratios to analyze data and identify trends. From calculating proportions to analyzing rates of change, ratios are essential for statistical analysis.
17.1. Proportions
Proportions are used to express the fraction of a population that has a certain characteristic. They are calculated by dividing the number of individuals with the characteristic by the total population size.
17.2. Rates of Change
Rates of change measure how quickly a quantity is changing over time. They are calculated by dividing the change in the quantity by the time taken for the change to occur.
17.3. Using Ratios to Make Inferences
Ratios can be used to make inferences about a population based on a sample. By analyzing the ratios in the sample, you can estimate the ratios in the population.
18. Practical Tips for Mastering Ratio Problems
Mastering ratio problems requires practice and a solid understanding of the underlying concepts. Here are some practical tips to help you improve your ratio skills:
18.1. Practice Regularly
The more you practice ratio problems, the better you will become at solving them. Set aside time each day to work on ratio problems and track your progress.
18.2. Understand the Concepts
Make sure you have a solid understanding of the basic concepts of ratios, proportions, and rates. This will make it easier to solve more complex problems.
18.3. Use Real-World Examples
Relate ratio problems to real-world examples to make them more meaningful and easier to understand. This will help you see how ratios are used in everyday life.
19. Addressing Common Misconceptions About Ratios
There are several common misconceptions about ratios that can lead to errors and confusion. Here are some of the most common misconceptions and how to avoid them:
19.1. Ratios Are Always Fractions
While ratios can be expressed as fractions, they can also be expressed as decimals, percentages, or using a colon. It’s important to understand that ratios are not always fractions.
19.2. Ratios Must Be in Simplest Form
While it’s often helpful to simplify ratios to their simplest form, it’s not always necessary. The most important thing is to maintain the correct proportions and make accurate comparisons.
19.3. Ratios Only Compare Whole Numbers
Ratios can compare any two quantities, including fractions, decimals, and mixed numbers. It’s important to be comfortable working with ratios involving different types of numbers.
20. Final Thoughts: Embracing the Power of Ratios
Ratios are a powerful tool for comparing quantities, analyzing data, and making informed decisions. By understanding the basic concepts of ratios, proportions, and rates, you can unlock their potential and improve your problem-solving skills.
20.1. The Ubiquity of Ratios in Daily Life
Ratios are everywhere in daily life, from cooking and shopping to finance and science. By recognizing and understanding ratios, you can make better decisions and improve your understanding of the world around you.
20.2. Encouragement to Explore Further
We encourage you to continue exploring the world of ratios and discover their many applications. By practicing and applying your knowledge, you can become a master of ratios and unlock their full potential.
20.3. A Final Word from COMPARE.EDU.VN
At COMPARE.EDU.VN, we are committed to providing you with the tools and resources you need to make informed decisions. Explore our website to discover more ways to use ratios and other mathematical concepts to improve your life.
Ready to make smarter choices? Visit COMPARE.EDU.VN today and discover how our comprehensive comparisons can help you make informed decisions. Whether you’re comparing products, services, or ideas, COMPARE.EDU.VN provides the insights you need to choose with confidence. Contact us at 333 Comparison Plaza, Choice City, CA 90210, United States, Whatsapp: +1 (626) 555-9090 or visit our website COMPARE.EDU.VN.
Frequently Asked Questions (FAQs) About Ratios
1. What is a ratio?
A ratio is a ratio that compares two quantities, showing their relative sizes. It can be expressed as a fraction, with a colon, or using words.
2. How do you simplify a ratio?
To simplify a ratio, divide both quantities by their greatest common divisor (GCD).
3. What is a proportion?
A proportion is an equation stating that two ratios are equal. It is often written as a/b = c/d.
4. What is a unit rate?
A unit rate is a ratio that compares a quantity to one unit of another quantity. For example, miles per hour is a unit rate.
5. How do you calculate a unit price?
To calculate the unit price, divide the total price by the number of units.
6. What are equivalent ratios?
Equivalent ratios are ratios that have the same value, even though they may be expressed with different numbers.
7. How do you scale a recipe using ratios?
To scale a recipe, multiply or divide all ingredient quantities by the same scaling factor to maintain the correct proportions.
8. What are financial ratios used for?
Financial ratios are used to analyze a company’s financial performance and assess its financial health.
9. How do ratios relate to geometry?
Ratios are used in geometry to understand the relationships between shapes and sizes, such as similar figures and trigonometric ratios.
10. Where can I find reliable comparisons to make informed decisions?
Visit compare.edu.vn for comprehensive comparisons of products, services, and ideas to help you make the best choices.