A Fraction That Compares Two Quantities Measured In Units is called a rate. At compare.edu.vn, we help you understand and utilize rates effectively. Understanding rates is crucial for making informed decisions in various real-life scenarios, from calculating speed to comparing prices. This guide will provide a comprehensive look at rates, including how they are written, simplified, and used in practical applications.
1. Understanding Ratios and Their Representation
Ratios are fundamental to understanding rates. A ratio compares two quantities by division, illustrating the relationship between them.
1.1 Defining Ratios
A ratio compares two quantities using division, expressed in various ways:
- Words: “3 to 4”
- Fraction: (frac{3}{4})
- Colon: 3:4
Simplifying a ratio involves reducing it to its simplest form, similar to simplifying fractions.
For instance, if a bakery has 15 chocolate cupcakes and 25 vanilla cupcakes, the ratio of chocolate to vanilla cupcakes is:
(frac{text{chocolate cupcakes}}{text{vanilla cupcakes}} = frac{15}{25})
Simplifying this ratio:
(frac{15}{25} = frac{15 div 5}{25 div 5} = frac{3}{5})
This can be expressed as “3 to 5” or “3:5,” meaning for every 3 chocolate cupcakes, there are 5 vanilla cupcakes.
1.2 Example: Basketball Player’s Shots
Consider a basketball player who takes 60 shots and makes 36. The ratio of shots made to shots taken is:
(frac{text{shots made}}{text{shots taken}} = frac{36}{60})
Simplifying the ratio:
(frac{36}{60} = frac{36 div 12}{60 div 12} = frac{3}{5})
This can be written as 3:5 or 3 to 5.
1.3 Comparing Calories in Fast Food
Suppose one fast food restaurant’s burger has 600 calories, while another’s has 400 calories. Comparing the calories:
(frac{text{calories in Restaurant A}}{text{calories in Restaurant B}} = frac{600}{400})
Simplifying the ratio:
(frac{600}{400} = frac{600 div 200}{400 div 200} = frac{3}{2})
This can be expressed as 3:2, showing that Restaurant A’s burger has 1.5 times the calories of Restaurant B’s burger.
1.4 Comparing Part to Part vs. Part to Whole
In a group of 30 people, 12 are adults and 18 are children. The ratio of adults to children is:
(frac{text{adults}}{text{children}} = frac{12}{18})
Simplifying the ratio:
(frac{12}{18} = frac{12 div 6}{18 div 6} = frac{2}{3})
The ratio of adults to the total number of people is:
(frac{text{adults}}{text{total people}} = frac{12}{30})
Simplifying this ratio:
(frac{12}{30} = frac{12 div 6}{30 div 6} = frac{2}{5})
This shows the distinction between comparing a part to a part versus a part to the whole.
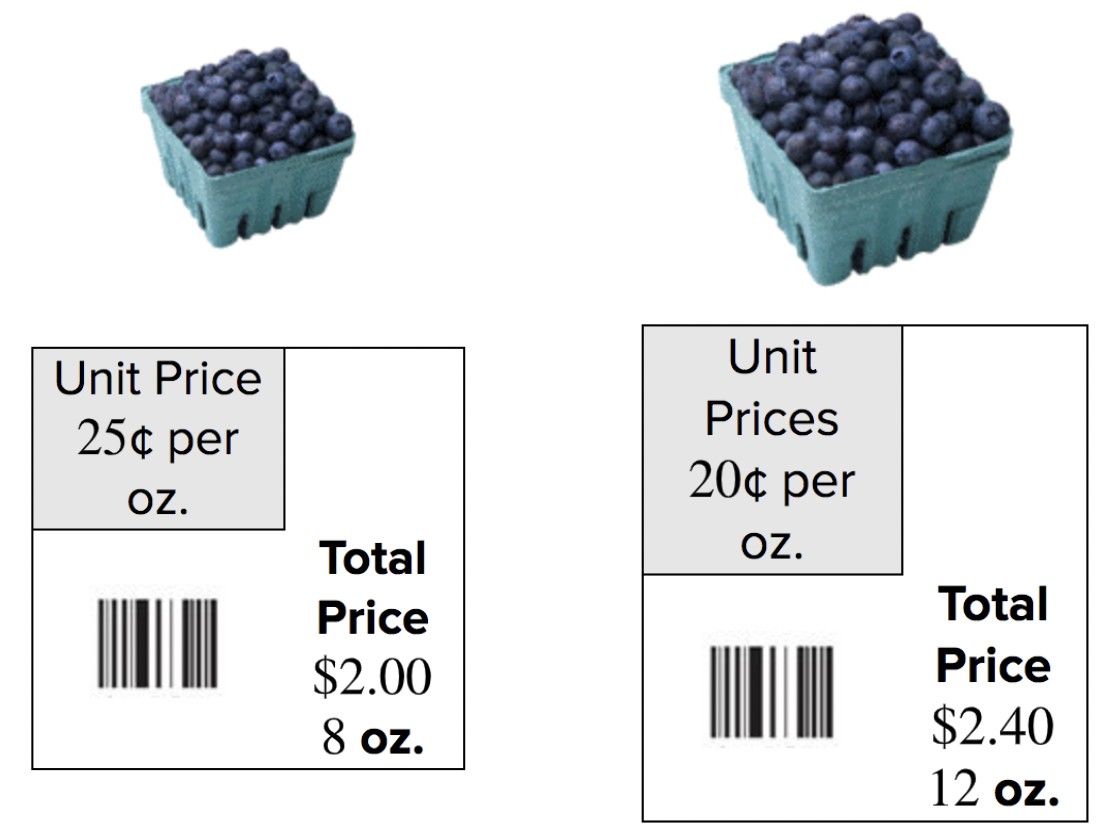Comparing Ratios
Image alt text: Comparison of two blueberry containers showing prices and weights to illustrate the concept of unit price and value.
2. Introduction to Rates: Definition and Examples
Rates are a specific type of ratio that compares two quantities with different units of measure. They are vital for understanding various real-world scenarios, such as speed, wages, and prices.
2.1 Defining Rates
A rate is a ratio comparing two different quantities with different units. Common examples include:
- Miles per hour (speed)
- Dollars per hour (wage)
- Dollars per gallon (price)
The term “per” indicates a rate. Rates can be written in words, with a colon, or as a fraction, always including the units.
For example, if a company needs 5 buses to transport 250 employees, the rate can be written as:
- 5 buses per 250 people
- 5 buses : 250 people
- (frac{5 text{ buses}}{250 text{ people}})
Simplifying this rate:
(frac{5 text{ buses}}{250 text{ people}} = frac{5 div 5}{250 div 5} = frac{1 text{ bus}}{50 text{ people}})
This means one bus is needed for every 50 people.
2.2 Example: Phone Lines to Employees
If a company has 10 phone lines for 40 employees, the rate is:
(frac{10 text{ phone lines}}{40 text{ employees}})
Simplifying the rate:
(frac{10 text{ phone lines}}{40 text{ employees}} = frac{10 div 10}{40 div 10} = frac{1 text{ phone line}}{4 text{ employees}})
This indicates one phone line for every four employees.
2.3 Flight Attendants to Passengers
If an airline assigns 8 flight attendants for 320 passengers, the rate is:
(frac{8 text{ flight attendants}}{320 text{ passengers}})
Simplifying the rate:
(frac{8 text{ flight attendants}}{320 text{ passengers}} = frac{8 div 8}{320 div 8} = frac{1 text{ flight attendant}}{40 text{ passengers}})
This means one flight attendant for every 40 passengers.
3. Unit Rates: Measuring Quantities Against a Single Unit
A unit rate simplifies comparisons by measuring a quantity against one unit, making it easier to understand and apply in various scenarios.
3.1 Defining Unit Rates
A unit rate compares a quantity to one unit of measure. For example, speed is often expressed as a unit rate, such as miles per hour. The denominator of a unit rate is always one.
If a car travels 400 miles in 8 hours, the unit rate is found by determining the miles traveled in one hour:
(frac{400 text{ miles}}{8 text{ hours}} = frac{400 div 8}{8 div 8} = frac{50 text{ miles}}{1 text{ hour}})
This is commonly written as 50 miles per hour.
3.2 Passengers Per Subway Car
If a subway train has 450 passengers in 9 cars, the unit rate of passengers per car is:
(frac{450 text{ passengers}}{9 text{ cars}} = frac{450 div 9}{9 div 9} = frac{50 text{ passengers}}{1 text{ car}})
The unit rate is 50 passengers per subway car.
3.3 Calculating Words Per Minute
Suppose a student types 600 words in 12 minutes. The unit rate of words per minute is:
(frac{600 text{ words}}{12 text{ minutes}} = frac{600 div 12}{12 div 12} = frac{50 text{ words}}{1 text{ minute}})
The unit rate is 50 words per minute.
4. Unit Prices: Comparing Costs per Single Item
A unit price is a critical tool for consumers, allowing for easy comparison of the cost of goods by expressing the price of a single unit.
4.1 Defining Unit Prices
A unit price is a unit rate that expresses the price of one unit of a product, facilitating price comparisons.
For instance, when comparing two bottles of juice, it’s easier to compare the cost per ounce rather than the total price of different-sized bottles.
If a 4-pack of juice costs $6.00, the unit price is:
(frac{$6.00}{4 text{ bottles}} = frac{$6.00 div 4}{4 div 4} = frac{$1.50}{1 text{ bottle}})
The unit price is $1.50 per bottle.
4.2 Comparing Tissue Boxes
A 5-pack of tissues costs $8.00, while a single box costs $1.75. The unit price of the 5-pack is:
(frac{$8.00}{5 text{ boxes}} = frac{$8.00 div 5}{5 div 5} = frac{$1.60}{1 text{ box}})
Comparing this to the single box at $1.75, the 5-pack is the better deal at $1.60 per box.
4.3 Cost of Sirloin Tips
If 5 pounds of sirloin tips cost $35, the unit price per pound is:
(frac{$35.00}{5 text{ pounds}} = frac{$35.00 div 5}{5 div 5} = frac{$7.00}{1 text{ pound}})
The unit price of the sirloin tips is $7.00 per pound.
4.4 Comparing Crackers
Brand A crackers cost $1.20 for 10 ounces, while Brand B costs $1.65 for 15 ounces. For Brand A, the unit price is:
(frac{$1.20}{10 text{ ounces}} = frac{$1.20 div 10}{10 div 10} = frac{$0.12}{1 text{ ounce}})
For Brand B, the unit price is:
(frac{$1.65}{15 text{ ounces}} = frac{$1.65 div 15}{15 div 15} = frac{$0.11}{1 text{ ounce}})
Brand B has a lower unit price at 11 cents per ounce, making it the better value.
5. Practical Applications of Ratios and Rates
Ratios and rates are essential tools in everyday problem-solving, providing a framework for understanding and comparing different quantities and measures. Here are several practical applications where the understanding of ratios and rates can be incredibly beneficial.
5.1 Cooking and Baking
In culinary arts, ratios and rates are used to scale recipes, ensuring the correct proportions of ingredients are maintained. For example, a cake recipe might specify a ratio of flour to sugar as 3:2. If you want to double the recipe, you need to maintain this ratio by doubling both quantities. Similarly, rates can be used to calculate cooking times based on the weight of the food. For instance, a roast might require 20 minutes of cooking time per pound.
5.2 Travel and Transportation
Rates are commonly used to calculate speed, fuel efficiency, and travel times. If a car travels 300 miles in 5 hours, the average speed can be calculated as a rate:
[
frac{300 text{ miles}}{5 text{ hours}} = 60 text{ miles per hour}
]
This rate helps in estimating travel times for long journeys. Additionally, fuel efficiency, measured in miles per gallon (MPG), is a rate that helps drivers compare the fuel consumption of different vehicles.
5.3 Personal Finance
Ratios and rates play a crucial role in managing personal finances, including budgeting, saving, and investing. For example, the debt-to-income ratio is a key metric used by lenders to assess the risk of providing a loan. It is calculated as the ratio of total debt payments to total income. Similarly, interest rates on loans and investments are rates that determine the cost of borrowing and the return on investment.
5.4 Healthcare and Medicine
In healthcare, ratios and rates are used for various purposes, such as calculating medication dosages, infection rates, and patient-to-nurse ratios. For example, a doctor might prescribe a medication at a rate of 5 mg per kilogram of body weight. In epidemiology, incidence rates (the number of new cases of a disease per population at risk) and prevalence rates (the total number of cases of a disease in a population) are used to monitor and control the spread of diseases.
5.5 Environmental Science
Environmental scientists use ratios and rates to measure and analyze various environmental parameters, such as pollution levels, deforestation rates, and species population densities. For example, the concentration of pollutants in water or air is often expressed as a rate (e.g., parts per million or PPM). Deforestation rates, measured as the percentage of forest area lost per year, help assess the impact of human activities on ecosystems.
5.6 Sports and Fitness
In sports, ratios and rates are used to analyze player performance, calculate statistics, and set fitness goals. For example, a basketball player’s shooting percentage is a ratio of successful shots to total shots taken. In fitness, heart rate is often expressed as beats per minute (BPM), and exercise intensity can be measured as a percentage of maximum heart rate.
5.7 Business and Economics
Businesses use ratios and rates extensively for financial analysis, marketing, and operations management. Financial ratios, such as the price-to-earnings ratio (P/E ratio) and return on equity (ROE), are used to evaluate a company’s financial performance and compare it to competitors. Marketing professionals use conversion rates (the percentage of website visitors who complete a desired action, such as making a purchase) to assess the effectiveness of marketing campaigns.
5.8 Construction and Engineering
Engineers use ratios and rates in designing structures, calculating material requirements, and assessing safety factors. For example, the slope of a roof is often expressed as a ratio of rise to run. In structural engineering, safety factors are calculated as the ratio of a structure’s ultimate strength to the maximum expected load.
5.9 Agriculture
In agriculture, ratios and rates are used to optimize crop yields, manage resources, and control pests. For example, fertilizer application rates are calculated based on the nutrient requirements of the crop and the nutrient content of the soil. Irrigation rates, measured as the amount of water applied per unit area, help ensure efficient water use.
5.10 Technology and Computing
In technology, ratios and rates are used to measure data transfer speeds, processing power, and network performance. For example, data transfer speeds are often expressed as megabits per second (Mbps) or gigabits per second (Gbps). Processing power can be measured in terms of clock speed (e.g., gigahertz or GHz) and the number of instructions executed per second.
By understanding and applying ratios and rates in these diverse fields, individuals can make more informed decisions, solve complex problems, and achieve their goals more effectively.
6. Common Mistakes to Avoid When Working with Ratios and Rates
Working with ratios and rates can be straightforward, but there are several common mistakes that can lead to incorrect conclusions. Being aware of these pitfalls can help ensure accuracy in calculations and interpretations. Here are some of the most frequent errors to avoid:
6.1. Mixing Up the Order of Quantities
One of the most common mistakes is mixing up the order of quantities in a ratio or rate. The order is crucial because it defines the relationship being expressed. For example, the ratio of apples to oranges is different from the ratio of oranges to apples. Always ensure that the quantities are in the correct order as specified in the problem or context.
Example:
- Correct: The ratio of students to teachers is 20:1 (20 students for every 1 teacher).
- Incorrect: The ratio of students to teachers is 1:20 (1 teacher for every 20 students).
6.2. Failing to Include Units
When working with rates, it is essential to include the units of measure. Rates compare quantities with different units, and omitting these units can lead to misunderstandings and incorrect interpretations. For example, stating a speed as “60” without specifying “miles per hour” or “kilometers per hour” is incomplete and ambiguous.
Example:
- Correct: The car is traveling at a speed of 60 miles per hour (mph).
- Incorrect: The car is traveling at a speed of 60.
6.3. Not Simplifying Ratios and Rates
Failing to simplify ratios and rates can make them harder to understand and compare. Simplifying involves reducing the ratio or rate to its lowest terms by dividing both quantities by their greatest common factor. This makes the relationship clearer and easier to work with.
Example:
- Unsimplified: The ratio of flour to sugar is 4:2.
- Simplified: The ratio of flour to sugar is 2:1 (after dividing both quantities by 2).
6.4. Incorrectly Calculating Unit Rates
Unit rates are used to compare quantities based on a single unit of measure. A common mistake is to divide the quantities in the wrong order when calculating a unit rate. Ensure that you are dividing by the quantity you want to express as “per one unit” of the other quantity.
Example:
- Correct: To find the cost per item, divide the total cost by the number of items: (frac{text{Total Cost}}{text{Number of Items}}).
- Incorrect: Dividing the number of items by the total cost.
6.5. Ignoring Common Factors
When simplifying ratios and rates, it is crucial to identify and divide by the greatest common factor (GCF) of the quantities. Failing to do so will result in a ratio or rate that is not fully simplified, making comparisons more difficult.
Example:
- Incomplete Simplification: The ratio of 12:18 is simplified to 6:9 (dividing by 2).
- Complete Simplification: The ratio of 12:18 is simplified to 2:3 (dividing by the GCF, which is 6).
6.6. Confusing Ratios and Proportions
Ratios express the relationship between two quantities, while proportions state that two ratios are equal. Confusing these concepts can lead to incorrect problem-solving. Proportions are used to find unknown quantities when two ratios are known to be equivalent.
Example:
- Ratio: The ratio of boys to girls in a class is 3:2.
- Proportion: If the ratio of boys to girls is 3:2 and there are 12 boys, then the proportion (frac{3}{2} = frac{12}{x}) can be used to find the number of girls (x).
6.7. Misinterpreting Word Problems
Word problems often require careful reading to identify the correct quantities and their relationships. Misinterpreting the problem can lead to setting up the ratio or rate incorrectly. Always underline key information and define the quantities clearly before setting up the equation.
Example:
- Problem: “A recipe calls for 2 cups of flour for every 1 cup of sugar. How much flour is needed if you use 3 cups of sugar?”
- Correct Interpretation: The ratio of flour to sugar is 2:1. To find the amount of flour needed for 3 cups of sugar, set up the proportion (frac{2}{1} = frac{x}{3}) and solve for x.
6.8. Neglecting to Convert Units
When comparing rates, ensure that the units are consistent. Neglecting to convert units can lead to inaccurate comparisons. For example, if one rate is given in miles per hour and another in kilometers per hour, convert both to the same unit before comparing.
Example:
- Correct: Comparing 50 miles per hour to 80 kilometers per hour requires converting both to the same unit (e.g., converting kilometers to miles) before making the comparison.
6.9. Applying Ratios and Rates to Inappropriate Contexts
Ratios and rates are useful for comparing quantities, but they may not be applicable in all situations. Applying them to inappropriate contexts can lead to meaningless or misleading results. Always consider whether the relationship between the quantities makes sense to express as a ratio or rate.
Example:
- Inappropriate Use: Calculating the ratio of a person’s age to their height may not provide any meaningful information, as these two quantities are not directly related in a way that a ratio would explain.
By avoiding these common mistakes, you can ensure greater accuracy and effectiveness when working with ratios and rates in various mathematical and real-world applications.
7. Advanced Techniques for Using Ratios and Rates
Beyond the basics, several advanced techniques can enhance your ability to work with ratios and rates, allowing for more complex problem-solving and analysis. These techniques are particularly useful in fields such as finance, science, and engineering.
7.1. Using Ratios and Rates in Conversions
Conversion factors are rates that express the equivalence between different units of measure. They are used to convert quantities from one unit to another. Mastering the use of conversion factors is essential for accuracy in various calculations.
Example:
- Converting Miles to Kilometers: Since 1 mile is approximately equal to 1.609 kilometers, the conversion factor is (frac{1.609 text{ km}}{1 text{ mile}}). To convert 10 miles to kilometers:
[
10 text{ miles} times frac{1.609 text{ km}}{1 text{ mile}} = 16.09 text{ km}
]
7.2. Scaling Recipes and Formulas
In cooking, chemistry, and other fields, it is often necessary to scale recipes or formulas while maintaining the correct proportions of ingredients. Ratios and rates are used to adjust the quantities accurately.
Example:
- Scaling a Recipe: A cake recipe calls for a flour-to-sugar ratio of 3:2. If you want to make a larger cake using 6 cups of flour, you can set up a proportion to find the amount of sugar needed:
[
frac{3 text{ cups flour}}{2 text{ cups sugar}} = frac{6 text{ cups flour}}{x text{ cups sugar}}
]
Solving for (x):
[
x = frac{2 times 6}{3} = 4 text{ cups sugar}
]
7.3. Analyzing Financial Ratios
Financial ratios are used to evaluate the performance and financial health of a company. These ratios are calculated using information from a company’s financial statements and provide insights into profitability, liquidity, solvency, and efficiency.
Example:
- Calculating the Current Ratio: The current ratio is a liquidity ratio that measures a company’s ability to pay its short-term obligations. It is calculated as:
[
text{Current Ratio} = frac{text{Current Assets}}{text{Current Liabilities}}
]
A higher current ratio indicates a stronger ability to meet short-term obligations.
7.4. Using Rates of Change in Calculus
In calculus, rates of change describe how one quantity changes in relation to another. Derivatives are used to find instantaneous rates of change, providing valuable information about the behavior of functions.
Example:
- Finding the Rate of Change of a Function: If (y = f(x)), the derivative (frac{dy}{dx}) represents the instantaneous rate of change of (y) with respect to (x). For example, if (f(x) = x^2), then (frac{dy}{dx} = 2x), which gives the rate of change of (y) at any point (x).
7.5. Applying Rates in Physics and Engineering
Rates are fundamental in physics and engineering for describing motion, energy transfer, and various other phenomena.
Example:
- Calculating Velocity: Velocity is the rate of change of displacement with respect to time. If an object’s displacement is given by (s(t)), then its velocity (v(t)) is:
[
v(t) = frac{ds}{dt}
]
This rate provides information about how fast the object is moving and in what direction.
7.6. Using Proportions and Ratios in Statistics
Statistics relies heavily on proportions and ratios for analyzing data and making inferences about populations.
Example:
- Calculating Sample Proportions: If a sample of 100 people includes 60 who prefer Brand A, the sample proportion is:
[
hat{p} = frac{60}{100} = 0.6
]
This proportion can be used to estimate the proportion of the entire population that prefers Brand A.
7.7. Applying Rates in Environmental Science
Environmental science uses rates to measure and analyze various environmental processes, such as pollution levels, deforestation rates, and species population changes.
Example:
- Calculating Deforestation Rate: If a forest area decreases from 10,000 square kilometers to 9,500 square kilometers in one year, the deforestation rate is:
[
text{Deforestation Rate} = frac{10,000 – 9,500}{10,000} times 100% = 5%
]
This rate indicates the percentage of forest area lost in one year.
7.8. Using Ratios and Rates in Network Analysis
In network analysis, ratios and rates are used to assess network performance, such as data transfer speeds and packet loss rates.
Example:
- Calculating Packet Loss Rate: If 1,000 packets are sent over a network and 20 are lost, the packet loss rate is:
[
text{Packet Loss Rate} = frac{20}{1,000} = 0.02 text{ or } 2%
]
This rate indicates the percentage of packets that fail to reach their destination.
By mastering these advanced techniques, you can leverage ratios and rates to solve complex problems and gain deeper insights in various fields.
8. Real-World Examples of Rate Applications
Understanding rates is not just an academic exercise; it’s a practical skill that is applicable to a variety of real-world scenarios. From everyday activities like shopping and driving to more complex situations in finance and healthcare, rates are essential for making informed decisions. Here are some compelling examples of how rates are used in real-world applications:
8.1. Grocery Shopping and Unit Pricing
When shopping for groceries, unit pricing helps consumers compare the cost of different-sized packages to determine the best value.
Example:
-
Comparing Cereal Prices:
- Brand A: $4.50 for a 15-ounce box ((frac{$4.50}{15 text{ ounces}} = $0.30 text{ per ounce}))
- Brand B: $6.00 for a 20-ounce box ((frac{$6.00}{20 text{ ounces}} = $0.30 text{ per ounce}))
In this case, both brands have the same unit price, so the choice might depend on other factors like brand preference or nutritional content.
8.2. Calculating Fuel Efficiency in Vehicles
Fuel efficiency, measured in miles per gallon (MPG), is a rate that helps drivers understand how far their vehicle can travel on a gallon of fuel.
Example:
- Calculating MPG: If a car travels 350 miles on 10 gallons of fuel, the fuel efficiency is:
[
text{MPG} = frac{350 text{ miles}}{10 text{ gallons}} = 35 text{ MPG}
]
This rate helps drivers compare the fuel consumption of different vehicles and estimate fuel costs for trips.
8.3. Determining Interest Rates on Loans
Interest rates, expressed as a percentage per year, determine the cost of borrowing money. Understanding interest rates is crucial for making informed decisions about loans and investments.
Example:
- Calculating Loan Interest: If you borrow $10,000 at an annual interest rate of 5%, the interest for one year is:
[
text{Interest} = $10,000 times 0.05 = $500
]
This rate helps borrowers understand the total cost of the loan over time.
8.4. Analyzing Patient-to-Nurse Ratios in Healthcare
Patient-to-nurse ratios are used in healthcare to ensure adequate staffing levels and quality patient care.
Example:
-
Comparing Patient-to-Nurse Ratios:
- Hospital A: 8 patients per nurse ((frac{8 text{ patients}}{1 text{ nurse}}))
- Hospital B: 6 patients per nurse ((frac{6 text{ patients}}{1 text{ nurse}}))
Hospital B has a lower patient-to-nurse ratio, which may indicate better patient care due to more individual attention from nurses.
8.5. Assessing Growth Rates in Business
Growth rates, expressed as a percentage increase over a period of time, are used to evaluate the performance of businesses and investments.
Example:
- Calculating Revenue Growth Rate: If a company’s revenue increases from $500,000 to $550,000 in one year, the growth rate is:
[
text{Growth Rate} = frac{$550,000 – $500,000}{$500,000} times 100% = 10%
]
This rate helps investors and business managers assess the company’s performance and potential for future growth.
8.6. Measuring Population Density in Ecology
Population density, expressed as the number of individuals per unit area, is used in ecology to study the distribution and abundance of species.
Example:
- Calculating Population Density: If there are 500 deer in a 10 square kilometer forest, the population density is:
[
text{Population Density} = frac{500 text{ deer}}{10 text{ km}^2} = 50 text{ deer per km}^2
]
This rate helps ecologists understand the carrying capacity of the environment and manage wildlife populations.
8.7. Determining Flow Rates in Engineering
Flow rates, expressed as the volume of fluid passing a point per unit time, are used in engineering to design and analyze fluid systems.
Example:
- Calculating Water Flow Rate: If 100 liters of water flow through a pipe in 5 minutes, the flow rate is:
[
text{Flow Rate} = frac{100 text{ liters}}{5 text{ minutes}} = 20 text{ liters per minute}
]
This rate helps engineers design pipes and pumps that can deliver the required flow for various applications.
8.8. Evaluating Production Rates in Manufacturing
Production rates, expressed as the number of units produced per unit time, are used in manufacturing to measure efficiency and productivity.
Example:
- Calculating Production Rate: If a factory produces 2,000 widgets in 8 hours, the production rate is:
[
text{Production Rate} = frac{2,000 text{ widgets}}{8 text{ hours}} = 250 text{ widgets per hour}
]
This rate helps managers identify areas for improvement and optimize production processes.
8.9. Assessing Infection Rates in Public Health
Infection rates, expressed as the number of new cases per population at risk over a specific period, are used in public health to monitor and control the spread of diseases.
Example:
- Calculating Infection Rate: If there are 50 new cases of the flu in a population of 10,000 people over one month, the infection rate is:
[
text{Infection Rate} = frac{50 text{ cases}}{10,000 text{ people}} = 0.005 text{ or } 0.5%
]
This rate helps public health officials assess the severity of an outbreak and implement appropriate interventions.
8.10. Measuring Data Transfer Rates in Computing
Data transfer rates, expressed as bits per second (bps) or bytes per second (Bps), are used in computing to measure the speed of data transmission.
Example:
- Calculating Download Speed: If a file of 10 megabytes (MB) downloads in 20 seconds, the average download speed is:
[
text{Download Speed} = frac{10 text{ MB}}{20 text{ seconds}} = 0.5 text{ MBps}
]
This rate helps users understand the speed of their internet connection and estimate download times for files.
By understanding these real-world examples, you can appreciate the practical significance of rates and their importance in various aspects of daily life and professional fields.
9. Understanding E-E-A-T and YMYL in the Context of Ratios and Rates
In the context of providing information about ratios and rates, it is essential to adhere to Google’s E-E-A-T (Experience, Expertise, Authoritativeness, and Trustworthiness) and YMYL (Your Money or Your Life) guidelines. These guidelines ensure that the information presented is accurate, reliable, and beneficial to the users, particularly when dealing with topics that can impact their financial or personal well-being. Here’s how these principles apply:
9.1. Experience (E)
Demonstrating practical experience with ratios and rates enhances the credibility of the content. Providing real-world examples and case studies where these concepts are applied helps users understand their relevance and utility.
- Example: Include personal anecdotes or examples from professional experiences where using ratios and rates led to successful outcomes, such as optimizing a budget, making a sound investment decision, or improving a business process.
- “In my experience as a financial advisor, teaching clients how to calculate and compare interest rates has been crucial for their long-term financial planning.”
9.2. Expertise (E)
Expertise involves having a high level of knowledge and skill in the subject matter. Presenting information about ratios and rates requires a clear understanding of mathematical principles, statistical methods, and practical applications.
- Example: Highlight any relevant qualifications, certifications, or educational background that demonstrates expertise in mathematics, finance, or a related field. Cite authoritative sources and academic research to support the content.
- “As a certified financial analyst with a degree in mathematics, I specialize in helping clients understand and apply financial ratios to make informed investment decisions.”
9.3. Authoritativeness (A)
Authoritativeness refers to being recognized as a reliable source of information by others in the field. This can be established through peer recognition, publications, citations, and endorsements from reputable organizations.
- Example: Mention any publications or presentations on ratios and rates that have been well-received by peers or recognized by industry experts. Highlight any affiliations with reputable organizations or institutions.
- “My work on financial ratios has been cited in several academic journals, and I am a frequent speaker at industry conferences on the topic of financial analysis.”
9.4. Trustworthiness (T)
Trustworthiness is about being honest, transparent, and reliable in providing information. It requires presenting accurate data, avoiding misleading claims, and disclosing any potential conflicts of interest.
- Example: Provide clear and accurate definitions of ratios and rates, along with step-by-step instructions for performing calculations. Disclose any potential biases or limitations in the data or analysis.
- “I am committed to providing unbiased and accurate information about ratios and rates, and I encourage readers to verify the data and analysis with other reliable sources.”
