What is A Fraction That Compares Two Quantities in Different Units?

A Fraction That Compares Two Quantities In Different Units is known as a rate. Rates are a specific type of ratio that expresses the relationship between two distinct units, such as miles per hour, cost per item, or students per class. Need to make informed comparisons? COMPARE.EDU.VN offers comprehensive guides. Explore unit rates and proportional relationships for better decision-making.

1. Understanding Ratios and Rates

1.1. What is a Ratio?

A ratio is a comparison of two quantities by division. It shows how much of one thing there is compared to another. Ratios can be written in several ways:

• Using the word “to”: For example, 3 to 4.
• As a fraction: For example, (frac{3}{4}).
• Using a colon: For example, 3:4.

A visual representation of a ratio, showing a comparison between two sets of objects

Example of Ratios

If there are 8 apples and 6 bananas in a fruit basket, the ratio of apples to bananas is 8 to 6, or (frac{8}{6}), which simplifies to (frac{4}{3}). This means for every 4 apples, there are 3 bananas.

1.2. What is a Rate?

A rate is a special type of ratio that compares two quantities with different units. The crucial aspect of a rate is that it involves different units of measurement. This distinguishes it from a simple ratio, which compares quantities of the same unit.

Key Characteristics of Rates:

• Different Units: Rates always involve two different units.
• Comparison by Division: Rates compare these different units through division.
• Real-World Applications: Rates are commonly used to describe real-world phenomena like speed, price, and consumption.

1.3. The Core Distinction: Ratios vs. Rates

While both ratios and rates involve comparing two quantities, the key difference lies in the units being compared:

• Ratios compare quantities with the same units.
• Rates compare quantities with different units.

For example, comparing the number of apples to the number of oranges is a ratio because both quantities are measured in the same unit (number of fruits). Comparing the distance traveled to the time taken (miles per hour) is a rate because distance and time are different units.

1.4. How to Express Rates

Rates can be expressed in several ways, similar to ratios:

• As a Fraction: This is the most common way, with the numerator representing one quantity and the denominator representing the other, each with its respective unit.
• Using the word “per”: For example, “miles per hour” or “dollars per item.”
• Using a Slanted Line: Representing “per,” such as $1.60/box.

2. What Makes a Rate a Fraction Comparing Different Units?

2.1. The Essence of Different Units

The fundamental characteristic of a rate is that it compares two quantities measured in different units. This difference in units provides essential context and meaning to the comparison.

Examples of Different Units in Rates:

• Distance and Time: Miles and hours (miles per hour)
• Cost and Quantity: Dollars and pounds (dollars per pound)
• Work and Time: Jobs and hours (jobs per hour)
• Consumption and Time: Liters and days (liters per day)

2.2. Why Different Units Matter

Using different units allows for a more informative comparison, providing insights into how one quantity changes with respect to another. It enables us to understand relationships that are not immediately apparent when comparing quantities of the same unit.

Benefits of Using Different Units:

• Practical Insights: Different units provide insights into real-world phenomena, such as efficiency, cost-effectiveness, and speed.
• Decision Making: Understanding rates helps in making informed decisions, such as choosing the best value for money or optimizing resource usage.
• Standardization: Rates allow for the standardization of measurements, making it easier to compare different scenarios.

2.3. Common Examples of Rates in Everyday Life

Rates are prevalent in everyday life, helping us make informed decisions and understand the world around us.

• Speed: Miles per hour (mph) or kilometers per hour (km/h) is used to measure how fast a vehicle is moving.
• Price: Dollars per pound ($/lb) or euros per kilogram (€/kg) is used to compare the cost of different products.
• Fuel Efficiency: Miles per gallon (mpg) or liters per kilometer (L/km) helps to understand how efficiently a vehicle uses fuel.
• Wage: Dollars per hour ($/hr) or euros per day (€/day) is used to determine how much someone earns for their work.

2.4. How Rates are Used in Various Fields

Rates are used extensively in various fields to analyze and understand data, make predictions, and optimize processes.

• Economics: Economists use rates to analyze inflation (percentage increase in prices per year), unemployment (percentage of unemployed people per total labor force), and economic growth (percentage increase in GDP per year).
• Healthcare: Healthcare professionals use rates to track disease prevalence (number of cases per population), mortality rates (number of deaths per population), and recovery rates (number of recovered patients per total patients).
• Engineering: Engineers use rates to calculate flow rates (volume of fluid per unit time), production rates (number of items produced per unit time), and efficiency rates (output per input).
• Environmental Science: Environmental scientists use rates to measure pollution levels (concentration of pollutants per volume of air or water), deforestation rates (area of forest lost per year), and species extinction rates (number of species lost per year).

3. Expressing Rates as Fractions

3.1. Why Fractions are a Natural Fit for Rates

Fractions provide a natural and intuitive way to express rates because they represent a division of two quantities. The numerator represents the amount of one quantity, while the denominator represents the amount of the other quantity.

Key Advantages of Using Fractions for Rates:

• Clarity: Fractions clearly show the relationship between two different units.
• Simplicity: Fractions can be easily simplified to their lowest terms, making the rate easier to understand.
• Comparability: Fractions allow for easy comparison of different rates by finding a common denominator.

3.2. How to Write a Rate as a Fraction

To write a rate as a fraction, follow these steps:

1. Identify the two quantities being compared.
2. Determine the units of each quantity.
3. Write the first quantity as the numerator and its unit.
4. Write the second quantity as the denominator and its unit.

Example:

If a car travels 240 miles in 4 hours, the rate can be written as:

(frac{240 text{ miles}}{4 text{ hours}})

3.3. Simplifying Rate Fractions

Just like regular fractions, rate fractions can be simplified by dividing both the numerator and the denominator by their greatest common factor. This makes the rate easier to understand and compare.

Example:

(frac{240 text{ miles}}{4 text{ hours}} = frac{240 div 4 text{ miles}}{4 div 4 text{ hours}} = frac{60 text{ miles}}{1 text{ hour}})

This simplified rate tells us that the car travels 60 miles per hour.

3.4. Examples of Expressing Different Rates as Fractions

Here are some examples of expressing different rates as fractions:

• Price of Apples: $3.00 for 6 apples can be written as (frac{$3.00}{6 text{ apples}}).
• Typing Speed: 400 words in 8 minutes can be written as (frac{400 text{ words}}{8 text{ minutes}}).
• Water Consumption: 15 liters in 3 days can be written as (frac{15 text{ liters}}{3 text{ days}}).
• Hourly Wage: $250 for 10 hours of work can be written as (frac{$250}{10 text{ hours}}).

4. Unit Rates: A Special Case of Rates

4.1. Definition of a Unit Rate

A unit rate is a rate where the denominator is one unit. Unit rates are used to express the amount of one quantity per single unit of another quantity.

Key Characteristics of Unit Rates:

• Denominator of One: The denominator of a unit rate is always 1.
• Standardized Comparison: Unit rates allow for easy comparison because they are standardized to one unit.
• Practical Applications: Unit rates are widely used in everyday life to make informed decisions.

4.2. How to Calculate a Unit Rate

To calculate a unit rate, divide both the numerator and the denominator of the rate fraction by the denominator. This will result in a fraction where the denominator is 1.

Example:

If a car travels 300 miles in 5 hours, the unit rate is:

(frac{300 text{ miles}}{5 text{ hours}} = frac{300 div 5 text{ miles}}{5 div 5 text{ hours}} = frac{60 text{ miles}}{1 text{ hour}})

This means the unit rate is 60 miles per hour.

4.3. Importance of Unit Rates for Comparison

Unit rates are essential for comparison because they provide a standardized measure that allows us to easily compare different scenarios.

Benefits of Using Unit Rates for Comparison:

• Easy Understanding: Unit rates are easy to understand because they express the amount of one quantity per single unit of another quantity.
• Direct Comparison: Unit rates allow for direct comparison of different rates without the need for complex calculations.
• Informed Decision Making: Unit rates help in making informed decisions by providing a clear understanding of the cost, speed, or efficiency per unit.

4.4. Real-World Examples of Unit Rates

Unit rates are used extensively in everyday life to make informed decisions.

• Price per Pound: Comparing the price of different brands of coffee by calculating the price per pound.
• Miles per Gallon: Determining the fuel efficiency of a car by calculating the number of miles it can travel per gallon of fuel.
• Words per Minute: Measuring typing speed by calculating the number of words typed per minute.
• Cost per Item: Comparing the cost of buying items in bulk versus individually by calculating the cost per item.

5. Finding Unit Prices

5.1. What is a Unit Price?

A unit price is a specific type of unit rate that expresses the cost of one unit of a product or service. Unit prices are commonly used in grocery stores and other retail settings to help consumers compare the cost of different items.

Key Characteristics of Unit Prices:

• Cost per Unit: Unit price represents the cost of one unit of a product or service.
• Easy Comparison: Unit prices allow for easy comparison of different brands and package sizes.
• Informed Purchasing Decisions: Unit prices help consumers make informed purchasing decisions by providing a clear understanding of the cost per unit.

5.2. Calculating Unit Prices

To calculate the unit price, divide the total cost of the product by the number of units.

Formula:

Unit Price = (frac{text{Total Cost}}{text{Number of Units}})

Example:

If a package of 6 apples costs $3.00, the unit price is:

Unit Price = (frac{$3.00}{6 text{ apples}} = $0.50 text{ per apple})

This means each apple costs $0.50.

5.3. Why Unit Prices are Important for Consumers

Unit prices are important for consumers because they allow for easy comparison of different brands and package sizes. This helps consumers make informed purchasing decisions and get the best value for their money.

Benefits of Using Unit Prices:

• Cost Comparison: Unit prices make it easy to compare the cost of different products.
• Value Assessment: Unit prices help consumers assess the value of different products.
• Budget Management: Unit prices assist in budget management by providing a clear understanding of the cost per unit.

5.4. Examples of Using Unit Prices to Compare Products

Here are some examples of using unit prices to compare different products:

• Cereal: Comparing the cost per ounce of different brands of cereal to determine which is the best value.
• Detergent: Comparing the cost per load of different brands of laundry detergent to find the most cost-effective option.
• Juice: Comparing the cost per liter of different brands of juice to make an informed purchasing decision.
• Snacks: Comparing the cost per serving of different snack items to manage your budget effectively.

6. Practice Problems: Applying Rates and Unit Prices

6.1. Problem 1: Calculating Speed

A train travels 450 miles in 6 hours. What is the average speed of the train in miles per hour?

Solution:

Speed = (frac{text{Distance}}{text{Time}} = frac{450 text{ miles}}{6 text{ hours}} = 75 text{ miles per hour})

The average speed of the train is 75 miles per hour.

6.2. Problem 2: Finding the Best Value

You are comparing two brands of orange juice:

• Brand A: 64 ounces for $4.80
• Brand B: 80 ounces for $5.60

Which brand offers the better value?

Solution:

Brand A:

Unit Price = (frac{$4.80}{64 text{ ounces}} = $0.075 text{ per ounce})

Brand B:

Unit Price = (frac{$5.60}{80 text{ ounces}} = $0.07 text{ per ounce})

Brand B offers the better value because it has a lower unit price ($0.07 per ounce) compared to Brand A ($0.075 per ounce).

6.3. Problem 3: Calculating Work Rate

An office assistant can type 560 words in 8 minutes. What is the typing rate in words per minute?

Solution:

Typing Rate = (frac{text{Number of Words}}{text{Time}} = frac{560 text{ words}}{8 text{ minutes}} = 70 text{ words per minute})

The typing rate is 70 words per minute.

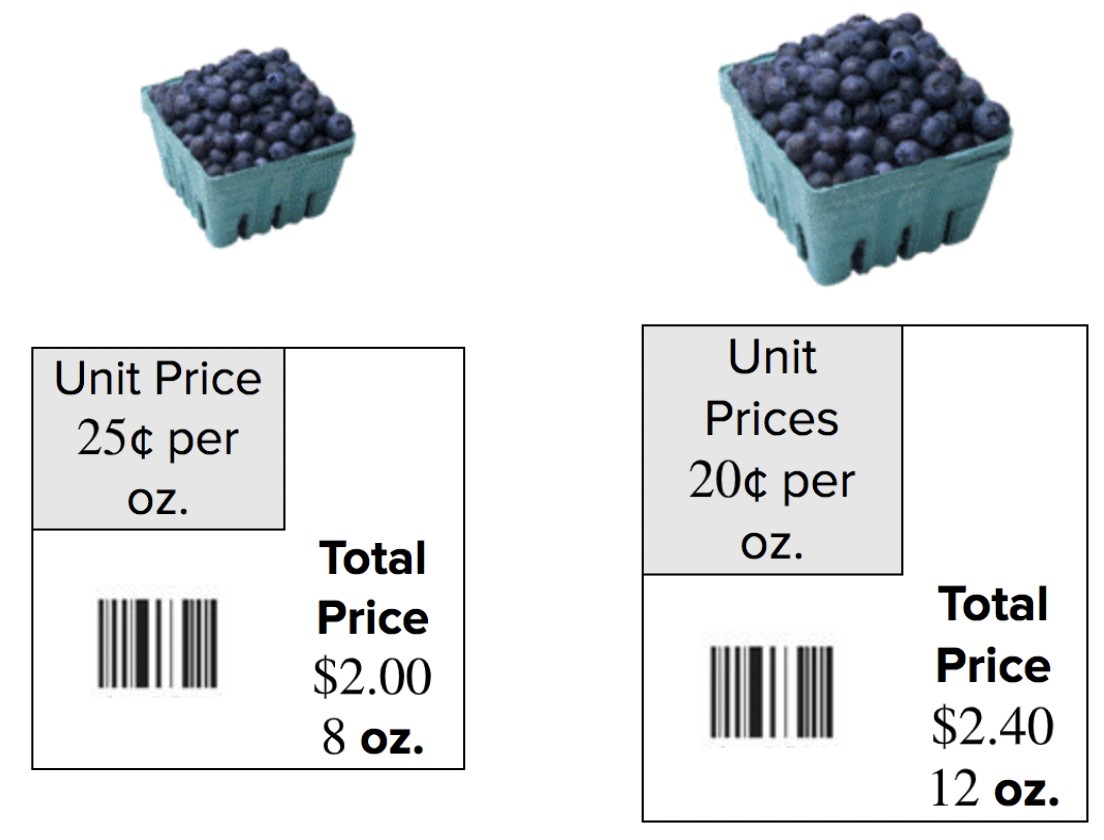
6.4. Problem 4: Comparing Prices

A store sells apples at $2.40 for 6 apples. Another store sells apples at $3.00 for 8 apples. Which store offers the better price per apple?

Solution:

Store 1:

Unit Price = (frac{$2.40}{6 text{ apples}} = $0.40 text{ per apple})

Store 2:

Unit Price = (frac{$3.00}{8 text{ apples}} = $0.375 text{ per apple})

Store 2 offers the better price per apple ($0.375 per apple) compared to Store 1 ($0.40 per apple).

7. Advanced Applications of Rates

7.1. Converting Rates

Sometimes, it is necessary to convert rates from one unit to another. This involves using conversion factors to change the units without changing the value of the rate.

Example:

Convert 60 miles per hour to feet per second.

1 mile = 5280 feet

1 hour = 3600 seconds

(frac{60 text{ miles}}{1 text{ hour}} times frac{5280 text{ feet}}{1 text{ mile}} times frac{1 text{ hour}}{3600 text{ seconds}} = frac{60 times 5280 text{ feet}}{3600 text{ seconds}} = 88 text{ feet per second})

So, 60 miles per hour is equal to 88 feet per second.

7.2. Using Rates in Proportional Relationships

Rates are often used in proportional relationships, where two quantities vary directly with each other. This means that if one quantity increases, the other quantity increases proportionally.

Example:

If a car travels at a constant speed of 60 miles per hour, the distance it travels is directly proportional to the time it travels. This relationship can be expressed as:

Distance = Speed x Time

If the car travels for 3 hours, the distance it covers is:

Distance = 60 miles per hour x 3 hours = 180 miles

7.3. Rates in Mixture Problems

Rates are also used in mixture problems, where two or more substances are combined to form a mixture. The concentration of each substance in the mixture can be expressed as a rate.

Example:

A chemist mixes 5 liters of a 20% acid solution with 3 liters of a 40% acid solution. What is the concentration of the resulting mixture?

Acid in the first solution = 5 liters x 20% = 1 liter

Acid in the second solution = 3 liters x 40% = 1.2 liters

Total acid in the mixture = 1 liter + 1.2 liters = 2.2 liters

Total volume of the mixture = 5 liters + 3 liters = 8 liters

Concentration of the mixture = (frac{2.2 text{ liters}}{8 text{ liters}} = 0.275 = 27.5%)

The concentration of the resulting mixture is 27.5%.

8. Why COMPARE.EDU.VN is Your Best Resource for Comparisons

8.1. Comprehensive and Objective Comparisons

COMPARE.EDU.VN provides comprehensive and objective comparisons between different products, services, and ideas. Our team of experts conducts thorough research and analysis to provide you with accurate and unbiased information.

8.2. Detailed Analysis of Pros and Cons

We list the pros and cons of each option, giving you a balanced view to make informed decisions. Our detailed analysis helps you understand the advantages and disadvantages of each choice, ensuring you consider all aspects before making a decision.

8.3. Comparison of Features, Specifications, and Prices

COMPARE.EDU.VN compares features, specifications, and prices to help you find the best fit for your needs and budget. We understand that different factors are important to different people, so we cover a wide range of criteria in our comparisons.

8.4. User Reviews and Expert Opinions

We provide user reviews and expert opinions to give you real-world insights. Hearing from others who have used the products or services can provide valuable perspectives to help you make your decision.

8.5. Helping You Make the Right Choice

COMPARE.EDU.VN is dedicated to helping you make the right choice by providing you with all the information you need in one place. Our goal is to simplify the comparison process and empower you to make confident decisions.

9. Conclusion: Mastering Rates and Unit Prices for Informed Decisions

Understanding rates and unit prices is essential for making informed decisions in various aspects of life. By expressing rates as fractions and calculating unit prices, you can easily compare different options and find the best value for your money. Websites like COMPARE.EDU.VN are valuable resources for providing detailed comparisons and helping you make the right choice.

Remember, a rate is a fraction that compares two quantities in different units, and a unit price is a rate that expresses the cost of one unit. Use these concepts to your advantage and make smart decisions every day.

10. Call to Action

Ready to make smarter decisions? Visit COMPARE.EDU.VN today for comprehensive comparisons and expert insights. Contact us at 333 Comparison Plaza, Choice City, CA 90210, United States, or via WhatsApp at +1 (626) 555-9090. Let COMPARE.EDU.VN help you find the best solutions for your needs.

FAQ: Frequently Asked Questions About Rates and Unit Prices

1. What is the difference between a ratio and a rate?

   A ratio compares two quantities with the same units, while a rate compares two quantities with different units.

2. How do you calculate a unit rate?

   To calculate a unit rate, divide both the numerator and the denominator of the rate fraction by the denominator to get a denominator of 1.

3. Why are unit prices important?

   Unit prices allow for easy comparison of different brands and package sizes, helping consumers make informed purchasing decisions.

4. Can you give an example of a rate?

   An example of a rate is miles per hour, which compares distance (miles) to time (hours).

5. How do you convert a rate from one unit to another?

   Use conversion factors to change the units without changing the value of the rate.

6. What is a unit price?

   A unit price is a specific type of unit rate that expresses the cost of one unit of a product or service.

7. How can COMPARE.EDU.VN help me make better decisions?

   COMPARE.EDU.VN provides comprehensive and objective comparisons, detailed analyses of pros and cons, comparisons of features and prices, and user reviews to help you make informed decisions.

8. What are some common examples of unit rates in everyday life?

   Common examples of unit rates include price per pound, miles per gallon, and words per minute.

9. How do rates relate to proportional relationships?

   Rates are often used in proportional relationships, where two quantities vary directly with each other.

10. Where can I find more information about rates and unit prices?

    Visit compare.edu.vn for more detailed information and comparisons.