A Fraction Compares by establishing its value relative to other fractions, indicating whether it is larger, smaller, or equal. At COMPARE.EDU.VN, we provide detailed comparisons that clarify these relationships. Discover the simple strategies for fraction comparison and enhance your comprehension of numerical values, ratios, and proportional relationships.
1. Understanding the Basics: What Does “A Fraction Compares” Really Mean?
When we say “a fraction compares,” we’re talking about the act of evaluating one fraction’s value in relation to another. This comparison is crucial in various real-life scenarios, from cooking and construction to finance and data analysis. A solid understanding of how a fraction compares helps in making informed decisions and solving problems effectively. According to research by the National Mathematics Advisory Panel, a strong foundation in fractions is predictive of success in algebra and more advanced mathematics. Therefore, understanding the principles of how a fraction compares is not merely an academic exercise but a practical skill that significantly impacts mathematical proficiency.
1.1. Defining a Fraction: Numerator and Denominator
A fraction represents a part of a whole, comprising two essential components: the numerator and the denominator. The numerator indicates the number of parts we are considering, while the denominator represents the total number of equal parts that make up the whole. Understanding the role of each part is essential for accurately comparing fractions.
1.2. Why Comparing Fractions Matters
Understanding how a fraction compares is vital in many everyday situations. Whether it’s figuring out which discount offers the best savings or calculating ingredient ratios in a recipe, the ability to compare fractions accurately makes problem-solving more efficient. Research from the University of California, Berkeley, highlights that individuals with better fraction proficiency demonstrate improved decision-making skills in various real-world contexts.
2. Methods for Comparing Fractions: A Comprehensive Guide
Several methods exist for effectively comparing fractions, each suitable for different scenarios and types of fractions. Here are some common methods, each detailed with steps and examples:
2.1. Comparing Fractions with the Same Denominator
When fractions share the same denominator, comparing them is straightforward. In this case, the fraction with the larger numerator is the greater fraction.
-
Step 1: Check that the denominators are the same.
-
Step 2: Compare the numerators.
-
Step 3: The fraction with the larger numerator is the larger fraction.
For example, comparing 3/7 and 5/7, since both fractions have the same denominator (7), we simply compare the numerators: 3 and 5. Because 5 > 3, the fraction 5/7 is larger than 3/7.
2.2. Comparing Fractions with the Same Numerator
If fractions have the same numerator but different denominators, the fraction with the smaller denominator is the larger. This is because the whole is divided into fewer parts, making each part larger.
-
Step 1: Verify that the numerators are the same.
-
Step 2: Compare the denominators.
-
Step 3: The fraction with the smaller denominator is the larger fraction.
For example, when comparing 2/5 and 2/3, both fractions have the same numerator (2). Since 3 < 5, the fraction 2/3 is larger than 2/5.
2.3. Comparing Fractions with Different Denominators
When fractions have different denominators, you need to find a common denominator before comparing them. The most common method is to find the Least Common Multiple (LCM) of the denominators.
2.3.1. Finding the Least Common Multiple (LCM)
The LCM is the smallest number that is a multiple of both denominators. This ensures that you can accurately convert both fractions to have the same denominator.
-
Step 1: Identify the denominators of the fractions you want to compare.
-
Step 2: List the multiples of each denominator until you find a common multiple.
-
Step 3: Identify the smallest common multiple.
For example, to find the LCM of 4 and 6:
- Multiples of 4: 4, 8, 12, 16, 20, 24, …
- Multiples of 6: 6, 12, 18, 24, 30, …
The LCM of 4 and 6 is 12.
2.3.2. Converting to Equivalent Fractions
Once you have the LCM, convert each fraction into an equivalent fraction with the LCM as the new denominator.
-
Step 1: Determine what factor you need to multiply each denominator by to get the LCM.
-
Step 2: Multiply both the numerator and the denominator of each fraction by that factor.
-
Step 3: Write the new equivalent fractions.
For example, to convert 1/4 and 2/6 to equivalent fractions with a denominator of 12:
-
For 1/4: Multiply both the numerator and the denominator by 3 (since 4 x 3 = 12).
1/4 x 3/3 = 3/12
-
For 2/6: Multiply both the numerator and the denominator by 2 (since 6 x 2 = 12).
2/6 x 2/2 = 4/12
-
2.3.3. Comparing the Converted Fractions
After converting the fractions to have the same denominator, compare the numerators to determine which fraction is larger.
-
Step 1: Check that the denominators of the converted fractions are the same.
-
Step 2: Compare the numerators.
-
Step 3: The fraction with the larger numerator is the larger fraction.
Continuing with the example, comparing 3/12 and 4/12, since 4 > 3, the fraction 4/12 (which is equivalent to 2/6) is larger than 3/12 (which is equivalent to 1/4).
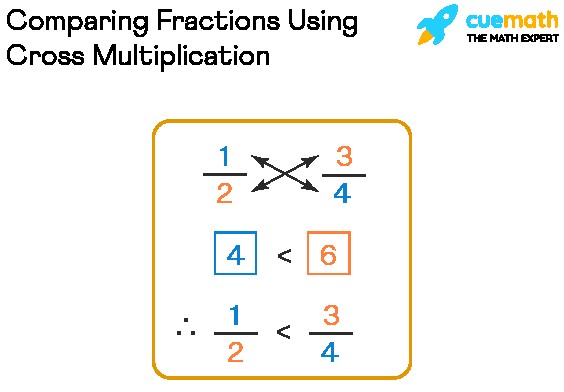
2.4. Cross Multiplication Method
Cross multiplication is a quick method for comparing two fractions without finding a common denominator.
-
Step 1: Write down the two fractions you want to compare.
-
Step 2: Multiply the numerator of the first fraction by the denominator of the second fraction.
-
Step 3: Multiply the numerator of the second fraction by the denominator of the first fraction.
-
Step 4: Compare the two products. The fraction associated with the larger product is the larger fraction.
For example, to compare 3/4 and 5/7:
- Multiply 3 (numerator of the first fraction) by 7 (denominator of the second fraction): 3 x 7 = 21
- Multiply 5 (numerator of the second fraction) by 4 (denominator of the first fraction): 5 x 4 = 20
Since 21 > 20, the fraction 3/4 is larger than 5/7.
2.5. Decimal Conversion Method
Converting fractions to decimals is another effective method for comparison, especially when dealing with complex fractions or using calculators.
-
Step 1: Divide the numerator of each fraction by its denominator to convert it to a decimal.
-
Step 2: Compare the decimal values.
-
Step 3: The fraction with the larger decimal value is the larger fraction.
For example, to compare 3/5 and 7/10:
- Convert 3/5 to a decimal: 3 ÷ 5 = 0.6
- Convert 7/10 to a decimal: 7 ÷ 10 = 0.7
Since 0.7 > 0.6, the fraction 7/10 is larger than 3/5.
2.6. Benchmarking
Benchmarking involves comparing fractions to a common reference point, such as 0, 1/2, or 1. This method is useful for quickly estimating and comparing fractions without precise calculations.
-
Step 1: Choose a benchmark (e.g., 0, 1/2, 1).
-
Step 2: Determine whether each fraction is less than, equal to, or greater than the benchmark.
-
Step 3: Compare the fractions based on their relationship to the benchmark.
For example:
- 5/8 is greater than 1/2 (since 1/2 = 4/8)
- 3/7 is less than 1/2 (since 1/2 = 3.5/7)
Therefore, 5/8 is larger than 3/7.
3. Real-World Applications of Comparing Fractions
Comparing fractions is not just a theoretical exercise; it has numerous practical applications in everyday life. Here are a few examples:
3.1. Cooking and Baking
In cooking and baking, recipes often require precise measurements of ingredients. Comparing fractions allows you to adjust recipes, scale quantities, and ensure the correct ratios are maintained. For example, if a recipe calls for 2/3 cup of flour and you want to make half the recipe, you need to calculate half of 2/3, which involves comparing and adjusting fractions.
3.2. Shopping and Discounts
When shopping, you often encounter discounts expressed as fractions or percentages. Comparing these fractions helps you determine which offer provides the greatest savings. For example, comparing a 1/4 discount to a 20% discount (which is 1/5) allows you to quickly assess which deal is better.
3.3. Construction and Measurement
In construction, measurements are often given in fractions of inches or feet. Comparing these fractions is essential for accurate cutting, fitting, and assembling materials. For instance, if you need to cut a piece of wood to be 3/8 inch shorter than another piece, you need to compare and subtract these fractions accurately.
3.4. Financial Planning
Fractions are commonly used in financial planning to represent portions of investments, interest rates, or debt. Comparing these fractions helps you make informed decisions about saving, investing, and managing your finances. For example, comparing different interest rates expressed as fractions helps you choose the best savings account or loan option.
4. Common Mistakes to Avoid When Comparing Fractions
Even with a good understanding of the methods, it’s easy to make mistakes when comparing fractions. Here are some common pitfalls to avoid:
4.1. Assuming Numerators Alone Determine Size
A common mistake is to assume that the fraction with the larger numerator is always the larger fraction, regardless of the denominator. This is only true when the denominators are the same. Always consider the denominator when comparing fractions.
4.2. Ignoring the Denominator When Numerators are Different
Similarly, it’s a mistake to ignore the denominator when the numerators are different. The denominator indicates how many parts the whole is divided into, so it significantly affects the size of each part. Always account for the denominator when comparing fractions.
4.3. Not Finding a Common Denominator
When fractions have different denominators, it’s essential to find a common denominator before comparing them. Failing to do so can lead to incorrect comparisons. Always convert fractions to equivalent forms with a common denominator before making any judgments about their relative sizes.
4.4. Errors in Cross Multiplication
Cross multiplication is a useful shortcut, but it’s important to perform the multiplication accurately. Ensure you multiply the correct numerators and denominators and compare the products correctly. Double-checking your calculations can prevent errors.
4.5. Misinterpreting Decimal Conversions
When converting fractions to decimals, be careful with the division. Ensure you divide the numerator by the denominator correctly, and pay attention to the decimal places. A small error in the decimal conversion can lead to an incorrect comparison.
5. Advanced Techniques for Fraction Comparison
For more complex scenarios, such as comparing multiple fractions or dealing with mixed numbers, advanced techniques can be helpful.
5.1. Comparing Multiple Fractions
To compare multiple fractions, convert all fractions to equivalent forms with a common denominator. Once they all have the same denominator, you can easily compare the numerators to determine their relative sizes.
5.2. Dealing with Mixed Numbers
A mixed number consists of a whole number and a fraction. To compare mixed numbers, first compare the whole number parts. If the whole numbers are different, the mixed number with the larger whole number is the larger number. If the whole numbers are the same, compare the fractional parts using one of the methods described above.
5.3. Using Fraction Simplification
Simplifying fractions before comparing them can make the process easier. Simplifying involves reducing a fraction to its lowest terms by dividing both the numerator and denominator by their greatest common factor (GCF). This can make the numbers smaller and easier to work with.
6. Best Practices for Mastering Fraction Comparison
Mastering fraction comparison requires practice and a solid understanding of the underlying concepts. Here are some best practices to help you improve your skills:
6.1. Practice Regularly
The more you practice comparing fractions, the more comfortable and confident you will become. Work through various examples and exercises to reinforce your understanding.
6.2. Use Visual Aids
Visual aids, such as fraction bars, pie charts, and number lines, can be helpful for visualizing fractions and comparing their sizes. These tools can make abstract concepts more concrete and easier to understand.
6.3. Relate Fractions to Real-World Scenarios
Relating fractions to real-world scenarios can help you see the practical relevance of fraction comparison. Think about how fractions are used in cooking, shopping, construction, and other everyday situations.
6.4. Review and Reinforce Basic Concepts
Make sure you have a solid understanding of the basic concepts of fractions, including numerators, denominators, equivalent fractions, and LCM. Review these concepts regularly to reinforce your knowledge.
6.5. Seek Help When Needed
If you’re struggling with fraction comparison, don’t hesitate to seek help from teachers, tutors, or online resources. There are many resources available to support your learning and help you overcome any challenges.
7. How COMPARE.EDU.VN Simplifies Fraction Comparisons
At COMPARE.EDU.VN, we understand that comparing fractions can be challenging. That’s why we provide tools and resources to simplify the process and help you make informed decisions. Our website offers:
7.1. Easy-to-Use Comparison Tools
Our comparison tools allow you to enter two or more fractions and instantly see their relative sizes. This can be particularly helpful for quickly comparing multiple fractions or checking your work.
7.2. Step-by-Step Guides and Tutorials
We provide detailed step-by-step guides and tutorials on various methods for comparing fractions. These resources are designed to make the process clear and easy to understand, regardless of your math background.
7.3. Real-World Examples and Case Studies
Our website includes real-world examples and case studies that illustrate how fraction comparison is used in everyday situations. These examples can help you see the practical relevance of the skills and motivate you to improve.
7.4. Expert Tips and Strategies
We offer expert tips and strategies for mastering fraction comparison. These tips are based on years of experience and are designed to help you avoid common mistakes and improve your accuracy and efficiency.
7.5. Interactive Practice Exercises
Our website features interactive practice exercises that allow you to test your skills and get immediate feedback. These exercises are designed to reinforce your understanding and help you build confidence.
8. FAQs About Comparing Fractions
Here are some frequently asked questions about comparing fractions:
8.1. What does comparing fractions mean?
Comparing fractions involves determining which fraction has a greater or lesser value, or if they are equal. It is a fundamental concept in mathematics with practical applications in everyday life.
8.2. What is the rule for comparing fractions with the same denominator?
When fractions have the same denominator, the fraction with the larger numerator is the larger fraction.
8.3. What is the rule for comparing fractions with the same numerator?
When fractions have the same numerator, the fraction with the smaller denominator is the larger fraction.
8.4. What are equivalent fractions?
Equivalent fractions are fractions that have different numerators and denominators but represent the same value. For example, 1/2 and 2/4 are equivalent fractions.
8.5. What is the easiest way to compare fractions?
The easiest way to compare fractions is often to convert them to decimals or to find a common denominator. Decimal conversion is particularly useful with calculators.
8.6. Why do we need to compare fractions?
Comparing fractions is important for developing number sense, understanding proportions, and making informed decisions in various real-world scenarios, such as cooking, shopping, and financial planning.
8.7. How do you compare fractions with different denominators?
To compare fractions with different denominators, find the Least Common Multiple (LCM) of the denominators and convert each fraction to an equivalent fraction with the LCM as the new denominator. Then, compare the numerators.
8.8. Can cross multiplication be used to compare fractions?
Yes, cross multiplication is a quick method for comparing two fractions. Multiply the numerator of each fraction by the denominator of the other fraction, and compare the products. The fraction associated with the larger product is the larger fraction.
8.9. What is benchmarking in fraction comparison?
Benchmarking involves comparing fractions to a common reference point, such as 0, 1/2, or 1, to quickly estimate and compare their relative sizes.
8.10. How can COMPARE.EDU.VN help with fraction comparison?
COMPARE.EDU.VN provides easy-to-use comparison tools, step-by-step guides, real-world examples, expert tips, and interactive practice exercises to simplify fraction comparison and help you make informed decisions.
9. Take the Next Step: Start Comparing Fractions Today
Understanding how a fraction compares is a valuable skill that can benefit you in many areas of life. By mastering the methods and avoiding common mistakes, you can confidently compare fractions and make informed decisions.
Ready to take your fraction comparison skills to the next level? Visit COMPARE.EDU.VN today to access our easy-to-use tools, step-by-step guides, and expert resources. Whether you’re a student, a professional, or simply someone who wants to improve your math skills, we have something for you.
Don’t struggle with fraction comparison any longer. Let COMPARE.EDU.VN help you unlock your full potential and make informed decisions with confidence.
Visit us today at COMPARE.EDU.VN or contact us at:
- Address: 333 Comparison Plaza, Choice City, CA 90210, United States
- WhatsApp: +1 (626) 555-9090
- Website: compare.edu.vn
Start comparing fractions today and experience the difference!