Comparing fractions is a fundamental skill in mathematics, essential for everyday situations from cooking and baking to understanding data and measurements. While comparing fractions with the same denominator is straightforward, things become a bit more complex when the denominators are different. This guide will walk you through various methods to confidently Compare Fractions With Different Denominators, ensuring you understand the ‘why’ behind each step.
Understanding Fractions: Numerator and Denominator
Before diving into comparing fractions with different denominators, let’s quickly recap what fractions are made of. A fraction represents a part of a whole and is written with two numbers separated by a line.
- Numerator: The number on the top, indicating how many parts you have.
- Denominator: The number on the bottom, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, ‘3’ is the numerator, and ‘4’ is the denominator. It means we have 3 parts out of a total of 4 equal parts.
The Challenge of Different Denominators
When comparing fractions like 1/2 and 3/4, it’s relatively easy to see that 3/4 is larger. But what about comparing 2/5 and 3/7? Here, the denominators are different, making a direct comparison of the numerators insufficient. We need to find a way to make the denominators “common” to accurately compare the fractions.
Methods to Compare Fractions with Different Denominators
Several effective methods allow us to compare fractions with different denominators. Let’s explore the most common and helpful ones:
Method 1: Finding a Common Denominator (Least Common Multiple – LCM)
This method is based on the principle that fractions can be easily compared when they have the same denominator. To achieve this, we find the Least Common Multiple (LCM) of the denominators. The LCM is the smallest number that is a multiple of both denominators.
Steps:
- Find the LCM of the denominators: Identify the denominators of the fractions you want to compare. Find the LCM of these denominators.
- Convert fractions to equivalent fractions with the LCM as the denominator: For each fraction, determine what number you need to multiply the original denominator by to get the LCM. Multiply both the numerator and the denominator by this number. This creates an equivalent fraction with the LCM as the new denominator.
- Compare the numerators: Once both fractions have the same denominator (the LCM), compare their numerators. The fraction with the larger numerator is the larger fraction.
Example: Compare 1/2 and 2/5
- LCM of denominators (2 and 5): The LCM of 2 and 5 is 10.
- Convert to equivalent fractions:
- For 1/2: To get a denominator of 10, multiply 2 by 5. So, multiply both numerator and denominator by 5: (1 × 5) / (2 × 5) = 5/10
- For 2/5: To get a denominator of 10, multiply 5 by 2. So, multiply both numerator and denominator by 2: (2 × 2) / (5 × 2) = 4/10
- Compare numerators: Now we compare 5/10 and 4/10. Since 5 > 4, then 5/10 > 4/10.
Therefore, 1/2 > 2/5.
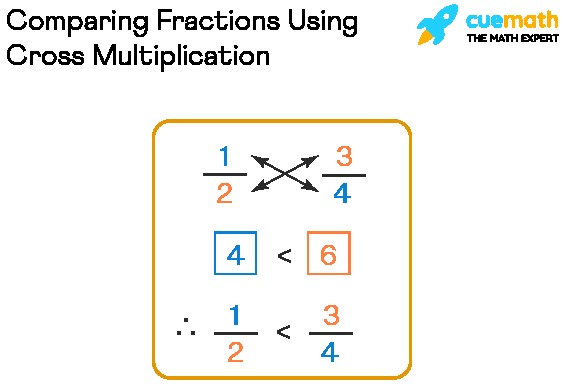
Method 2: Cross Multiplication
Cross multiplication is a quick and efficient method for comparing two fractions. It bypasses the need to explicitly find the LCM, making it a handy shortcut.
Steps:
- Cross multiply: Multiply the numerator of the first fraction by the denominator of the second fraction. Write the result to the right of the first fraction (or above it).
- Cross multiply again: Multiply the numerator of the second fraction by the denominator of the first fraction. Write the result to the right of the second fraction (or above it).
- Compare the products: Compare the two products you obtained in steps 1 and 2. The fraction corresponding to the larger product is the larger fraction.
Example: Compare 3/4 and 2/3
- Cross multiply (3/4 and 2/3): 3 (numerator of first fraction) × 3 (denominator of second fraction) = 9
- Cross multiply again (3/4 and 2/3): 2 (numerator of second fraction) × 4 (denominator of first fraction) = 8
- Compare products: Compare 9 and 8. Since 9 > 8, then 3/4 is the larger fraction.
Therefore, 3/4 > 2/3.
Method 3: Decimal Conversion
Another straightforward method is to convert each fraction into its decimal form. Once in decimal form, comparing them becomes as simple as comparing decimal numbers.
Steps:
- Convert fractions to decimals: Divide the numerator by the denominator for each fraction to convert it into a decimal.
- Compare the decimal values: Compare the decimal values obtained in step 1. The fraction with the larger decimal value is the larger fraction.
Example: Compare 5/8 and 7/12
- Convert to decimals:
- 5/8 = 0.625
- 7/12 ≈ 0.583 (rounded to three decimal places)
- Compare decimals: Compare 0.625 and 0.583. Since 0.625 > 0.583, then 5/8 is the larger fraction.
Therefore, 5/8 > 7/12.
Method 4: Visual Comparison
Visualizing fractions can be particularly helpful for understanding and comparing them, especially for beginners. Using visual aids like fraction bars or circles, we can represent fractions and compare their sizes visually.
Steps:
- Represent fractions visually: Draw or use pre-made fraction bars or circles to represent each fraction. Ensure the wholes are the same size.
- Compare shaded areas: Observe the shaded areas representing each fraction. The fraction with the larger shaded area is the larger fraction.
Example: Compare 4/6 and 4/8
By visualizing, we can see that 4/6 represents a larger portion of the whole compared to 4/8, even though they have the same numerator.
Step-by-Step Examples
Let’s work through a few more examples to solidify your understanding of comparing fractions with different denominators.
Example 1: Compare 2/3 and 5/8 using the LCM method.
- LCM of 3 and 8: LCM(3, 8) = 24
- Convert to equivalent fractions:
- 2/3 = (2 × 8) / (3 × 8) = 16/24
- 5/8 = (5 × 3) / (8 × 3) = 15/24
- Compare numerators: 16/24 and 15/24. Since 16 > 15, 2/3 > 5/8.
Example 2: Compare 4/7 and 5/9 using cross multiplication.
- Cross multiply: 4 × 9 = 36
- Cross multiply: 5 × 7 = 35
- Compare products: 36 and 35. Since 36 > 35, 4/7 > 5/9.
Example 3: Compare 1/4 and 3/10 using decimal conversion.
- Convert to decimals:
- 1/4 = 0.25
- 3/10 = 0.3
- Compare decimals: 0.25 and 0.3. Since 0.3 > 0.25, 3/10 > 1/4.
Tips and Tricks for Easier Comparison
- Benchmark Fractions: Sometimes, comparing to benchmark fractions like 1/2, 1/4, or 1 is helpful. For example, to compare 3/5 and 4/7, you might recognize that 3/5 is slightly more than 1/2 and 4/7 is slightly more than 1/2. To get a more precise comparison you would still use one of the methods above.
- Numerator Closeness to Denominator: If numerators are close to their denominators, the fraction is closer to 1 and likely larger than a fraction where the numerator is much smaller than the denominator.
Conclusion
Comparing fractions with different denominators might seem tricky initially, but by mastering these methods – finding a common denominator (LCM), cross multiplication, decimal conversion, and visualization – you can confidently determine which fraction is larger or smaller. Practice each method to find the one that works best for you and remember that understanding the underlying concept of fractions is key to successful comparison. Whether you’re working on homework or applying fractions in real-life scenarios, these techniques will prove invaluable.