Descriptive statistics offer powerful tools for summarizing and comparing data, and at COMPARE.EDU.VN, we provide comprehensive comparisons using these methods. By exploring measures of central tendency and variability, you can gain insights and make informed decisions. COMPARE.EDU.VN offers a wealth of resources for data analysis, statistical comparisons, and comparative insights.
1. Understanding the Power of Descriptive Statistics
Descriptive statistics are fundamental to understanding and comparing datasets. They provide a concise summary of the main features of a sample, allowing you to identify patterns, trends, and differences between groups. This section explores the core concepts and measures used in descriptive statistics.
1.1 What are Descriptive Statistics?
Descriptive statistics involve methods for organizing, summarizing, and presenting data in an informative way. Unlike inferential statistics, which aim to draw conclusions about a population based on a sample, descriptive statistics focus on describing the characteristics of the sample itself. This includes measures of central tendency, variability, and distribution shape.
1.2 Measures of Central Tendency
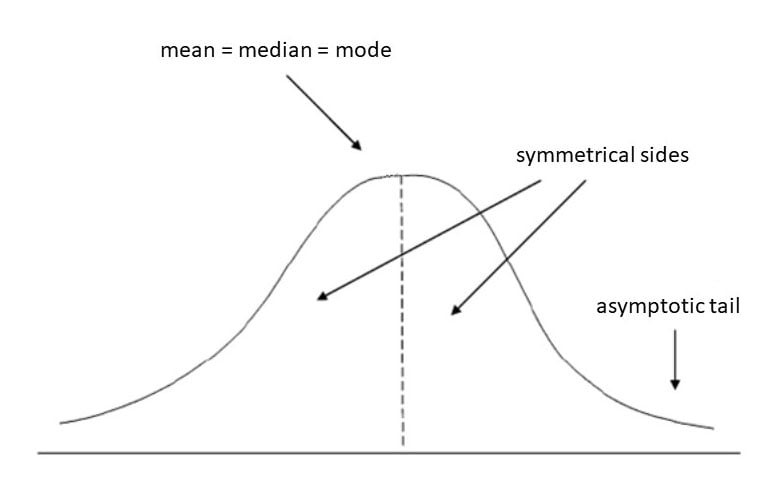
Measures of central tendency indicate the typical or central value in a dataset. The three most common measures are:
- Mean: The average value, calculated by summing all the values and dividing by the number of values. It’s sensitive to extreme values (outliers).
- Median: The middle value when the data is arranged in ascending order. It’s less sensitive to outliers than the mean.
- Mode: The most frequently occurring value in the dataset. It’s useful for identifying the most common category or value.
The choice of which measure to use depends on the nature of the data and the presence of outliers. For example, if the data is skewed or contains extreme values, the median might be a better choice than the mean.
1.3 Measures of Variability
Measures of variability describe the spread or dispersion of the data. Common measures include:
- Range: The difference between the maximum and minimum values. It’s a simple measure but can be greatly affected by outliers.
- Variance: The average of the squared differences from the mean. It quantifies the overall spread of the data.
- Standard Deviation: The square root of the variance. It provides a more interpretable measure of spread in the original units of the data.
- Interquartile Range (IQR): The difference between the 75th percentile (Q3) and the 25th percentile (Q1). It’s a robust measure of spread that is less sensitive to outliers.
Understanding variability is crucial when comparing datasets. A dataset with high variability will have a wider spread of values, while a dataset with low variability will have values clustered closer to the mean.
1.4 Visualizing Descriptive Statistics
Visualizing data can greatly enhance understanding and comparison. Common visualization techniques include:
- Histograms: Show the frequency distribution of a single variable.
- Box Plots: Display the median, quartiles, and outliers of a dataset.
- Scatter Plots: Show the relationship between two variables.
- Bar Charts: Compare the means or frequencies of different categories.
Visualizations can reveal patterns and trends that might not be apparent from numerical summaries alone. They are an essential tool for exploring and comparing data.
1.5 Importance of Descriptive Statistics in Decision-Making
Descriptive statistics play a crucial role in decision-making across various fields. By summarizing and comparing data, they provide insights that can inform decisions related to product development, marketing strategies, financial analysis, and more. For instance, businesses use descriptive statistics to analyze sales data, identify customer trends, and optimize pricing strategies. Researchers use them to summarize experimental results and compare different treatment groups.
2. Comparing Datasets: Techniques and Considerations
Comparing datasets effectively requires careful selection of appropriate descriptive statistics and visualization techniques. This section explores the methods for comparing different types of data and the factors to consider when interpreting the results.
2.1 Comparing Means
Comparing means is a common technique for assessing differences between groups. The most straightforward approach is to calculate the difference between the means and assess its magnitude. However, it’s important to consider the variability within each group when interpreting the difference. A large difference in means might not be statistically significant if the variability is high.
Statistical tests, such as t-tests and ANOVA, provide a more formal way to compare means and assess the statistical significance of the differences. These tests take into account the sample size, variability, and the magnitude of the difference in means.
2.2 Comparing Variances
Comparing variances is important when assessing the consistency or spread of data within different groups. A larger variance indicates greater variability.
Statistical tests, such as the F-test and Levene’s test, can be used to compare variances and assess whether the differences are statistically significant. These tests are particularly useful when comparing multiple groups or when the variances are unequal.
2.3 Comparing Distributions
Comparing distributions involves assessing the shape and spread of data across different groups. Visual techniques, such as histograms and box plots, are particularly useful for this purpose. They allow you to identify differences in skewness, kurtosis, and the presence of outliers.
Statistical tests, such as the Kolmogorov-Smirnov test and the Chi-square test, can be used to compare distributions and assess whether the differences are statistically significant. These tests are useful when comparing the overall shape of the distributions, not just the means and variances.
2.4 Considerations When Comparing Datasets
Several factors should be considered when comparing datasets:
- Sample Size: Larger sample sizes provide more reliable estimates of population parameters and increase the power of statistical tests.
- Data Type: The type of data (e.g., continuous, categorical) will influence the choice of appropriate descriptive statistics and comparison techniques.
- Outliers: Outliers can significantly affect the mean and variance, so it’s important to identify and address them appropriately.
- Statistical Significance: Statistical significance indicates whether the observed differences are likely due to chance or a real effect. However, it’s important to consider the practical significance of the findings as well. A statistically significant difference might not be meaningful in a real-world context.
2.5 Using Confidence Intervals for Comparison
Confidence intervals provide a range of values within which the true population parameter is likely to fall. Comparing confidence intervals can be a useful way to assess differences between groups. If the confidence intervals for two groups do not overlap, this suggests that the population means are likely different.
Confidence intervals can also be used to assess the precision of the estimates. A narrower confidence interval indicates a more precise estimate of the population parameter.
3. Advanced Descriptive Statistics for In-Depth Analysis
Beyond basic measures, advanced descriptive statistics offer deeper insights into data characteristics. This section explores techniques like skewness, kurtosis, and percentiles, enhancing comparative analysis.
3.1 Skewness and Kurtosis
Skewness and kurtosis describe the shape of a distribution:
- Skewness: Measures the asymmetry of the distribution. A symmetrical distribution has a skewness of 0. Positive skewness indicates a longer tail on the right, while negative skewness indicates a longer tail on the left.
- Kurtosis: Measures the peakedness of the distribution. A normal distribution has a kurtosis of 3. Higher kurtosis indicates a sharper peak and heavier tails, while lower kurtosis indicates a flatter peak and thinner tails.
Understanding skewness and kurtosis can provide valuable insights into the nature of the data. For example, a positively skewed distribution might indicate the presence of outliers or a concentration of values at the lower end of the scale.
3.2 Percentiles and Quartiles
Percentiles divide the data into 100 equal parts, while quartiles divide the data into four equal parts:
- Percentiles: The pth percentile is the value below which p% of the data falls. For example, the 25th percentile is the value below which 25% of the data falls.
- Quartiles: The first quartile (Q1) is the 25th percentile, the second quartile (Q2) is the 50th percentile (median), and the third quartile (Q3) is the 75th percentile.
Percentiles and quartiles provide a more detailed picture of the distribution of the data than just the mean and standard deviation. They can be used to identify the range of values within which a certain percentage of the data falls.
3.3 Standard Error of the Mean
The standard error of the mean (SEM) measures the precision of the sample mean as an estimate of the population mean. It is calculated by dividing the standard deviation by the square root of the sample size. A smaller SEM indicates a more precise estimate of the population mean.
The SEM is used to construct confidence intervals for the population mean. A 95% confidence interval is typically calculated as the sample mean plus or minus 1.96 times the SEM. This interval provides a range of values within which the true population mean is likely to fall with 95% confidence.
3.4 Harmonic and Geometric Means
The harmonic and geometric means are alternative measures of central tendency that are useful in specific situations:
- Harmonic Mean: The reciprocal of the average of the reciprocals of the values. It’s useful when dealing with rates or ratios.
- Geometric Mean: The nth root of the product of the values. It’s useful when dealing with data that grows exponentially.
For example, the harmonic mean might be used to calculate the average speed of a vehicle that travels the same distance at different speeds. The geometric mean might be used to calculate the average growth rate of an investment over multiple periods.
3.5 Using Descriptive Statistics to Identify Outliers
Outliers are extreme values that deviate significantly from the rest of the data. They can have a disproportionate impact on the mean and variance. Descriptive statistics can be used to identify outliers using several methods:
- Box Plots: Outliers are typically defined as values that fall below Q1 – 1.5 IQR or above Q3 + 1.5 IQR.
- Standard Deviation: Outliers are often defined as values that are more than 2 or 3 standard deviations away from the mean.
It’s important to investigate outliers to determine whether they are genuine values or the result of errors. If they are genuine values, they might provide valuable insights into the phenomenon being studied. However, if they are the result of errors, they should be corrected or removed from the data.
 Advanced descriptive statistics charts
Advanced descriptive statistics charts
3.6 Transforming Data to Improve Comparability
Sometimes, data transformations are necessary to improve the comparability of datasets. Common transformations include:
- Log Transformation: Used to reduce skewness and stabilize variance.
- Square Root Transformation: Used to reduce skewness and stabilize variance.
- Standardization (Z-score): Transforms the data to have a mean of 0 and a standard deviation of 1. This allows you to compare values from different datasets on a common scale.
The choice of transformation depends on the nature of the data and the goals of the analysis. It’s important to carefully consider the implications of each transformation before applying it.
4. Statistical Software for Descriptive Statistics
Statistical software packages offer powerful tools for calculating and visualizing descriptive statistics. This section explores popular software options and their capabilities.
4.1 SPSS
SPSS (Statistical Package for the Social Sciences) is a widely used statistical software package that offers a comprehensive set of descriptive statistics procedures. It allows you to calculate measures of central tendency, variability, skewness, kurtosis, and percentiles. It also provides tools for creating histograms, box plots, and other visualizations.
SPSS has a user-friendly interface and a wide range of statistical procedures, making it a popular choice for researchers and analysts. It also offers advanced features, such as data transformation and outlier detection.
4.2 R
R is a free and open-source statistical programming language that is widely used in academia and industry. It offers a vast collection of packages for calculating and visualizing descriptive statistics. R provides more flexibility and control than SPSS, but it requires more programming knowledge.
R is particularly well-suited for complex statistical analyses and data manipulation. It also has a strong community of users who contribute to the development of new packages and tools.
4.3 Excel
Excel is a spreadsheet software package that can be used to calculate basic descriptive statistics. It offers functions for calculating the mean, median, standard deviation, variance, and percentiles. Excel also provides tools for creating charts and graphs.
Excel is a convenient option for simple descriptive statistics calculations, but it is not as powerful or flexible as SPSS or R. It is also more prone to errors due to its lack of formal statistical procedures.
4.4 Python
Python is a versatile programming language with powerful libraries like NumPy, Pandas, and Matplotlib, which are used for data analysis and visualization. NumPy provides support for numerical operations, Pandas for data manipulation and analysis, and Matplotlib for creating static, interactive, and animated visualizations in Python.
Python is increasingly popular for data analysis due to its flexibility and extensive ecosystem of libraries. It is well-suited for both simple and complex statistical analyses.
4.5 Choosing the Right Software
The choice of which statistical software to use depends on several factors:
- Complexity of the Analysis: For simple descriptive statistics calculations, Excel might be sufficient. For more complex analyses, SPSS, R, or Python are better choices.
- Programming Knowledge: R and Python require more programming knowledge than SPSS or Excel.
- Cost: SPSS is a commercial software package, while R and Python are free and open-source.
- User Interface: SPSS has a user-friendly interface, while R and Python require more command-line interaction.
It’s important to consider these factors when choosing the right statistical software for your needs.
5. Practical Examples of Comparing with Descriptive Statistics
Descriptive statistics can be applied in various scenarios to make informed comparisons. This section illustrates practical applications across different domains.
5.1 Comparing Student Performance
A school administrator wants to compare the performance of students in two different teaching methods. They collect data on the test scores of students in each group and calculate the mean and standard deviation for each group.
By comparing the means, the administrator can assess which teaching method resulted in higher average test scores. By comparing the standard deviations, they can assess the variability of the test scores within each group.
The administrator can also create histograms or box plots to visualize the distribution of test scores in each group. This can help them identify differences in skewness, kurtosis, and the presence of outliers.
5.2 Comparing Product Sales
A marketing manager wants to compare the sales of two different products. They collect data on the monthly sales of each product and calculate the mean and standard deviation for each product.
By comparing the means, the manager can assess which product had higher average sales. By comparing the standard deviations, they can assess the variability of the sales of each product.
The manager can also create time series plots to visualize the trend of sales for each product over time. This can help them identify seasonal patterns or other trends.
5.3 Comparing Website Traffic
A web analyst wants to compare the traffic to two different websites. They collect data on the daily page views for each website and calculate the mean and standard deviation for each website.
By comparing the means, the analyst can assess which website had higher average traffic. By comparing the standard deviations, they can assess the variability of the traffic to each website.
The analyst can also create histograms or box plots to visualize the distribution of page views for each website. This can help them identify differences in skewness, kurtosis, and the presence of outliers.
5.4 Comparing Investment Returns
An investor wants to compare the returns of two different investments. They collect data on the annual returns for each investment and calculate the mean and standard deviation for each investment.
By comparing the means, the investor can assess which investment had higher average returns. By comparing the standard deviations, they can assess the riskiness of each investment.
The investor can also create scatter plots to visualize the relationship between the returns of the two investments. This can help them identify correlations or other patterns.
5.5 Comparing Customer Satisfaction
A customer service manager wants to compare the satisfaction of customers who used two different service channels. They collect data on the customer satisfaction scores for each channel and calculate the mean and standard deviation for each channel.
By comparing the means, the manager can assess which service channel resulted in higher average customer satisfaction. By comparing the standard deviations, they can assess the variability of the customer satisfaction scores for each channel.
The manager can also create bar charts to compare the distribution of customer satisfaction scores for each channel. This can help them identify differences in the percentage of customers who were very satisfied, satisfied, or dissatisfied.
6. Common Pitfalls to Avoid When Comparing Data
Comparing data requires careful attention to detail to avoid misleading conclusions. This section highlights common pitfalls and how to avoid them.
6.1 Ignoring Sample Size
Sample size plays a crucial role in the reliability of statistical estimates. Small sample sizes can lead to unstable estimates and increase the risk of drawing incorrect conclusions. It’s important to consider the sample size when interpreting the results of descriptive statistics and statistical tests.
Larger sample sizes provide more reliable estimates of population parameters and increase the power of statistical tests. If the sample size is too small, it might not be possible to detect statistically significant differences, even if they exist.
6.2 Overlooking Outliers
Outliers can have a disproportionate impact on the mean and variance. It’s important to identify and address outliers appropriately. Ignoring outliers can lead to misleading conclusions about the central tendency and variability of the data.
Outliers should be investigated to determine whether they are genuine values or the result of errors. If they are genuine values, they might provide valuable insights into the phenomenon being studied. However, if they are the result of errors, they should be corrected or removed from the data.
6.3 Misinterpreting Correlation
Correlation measures the strength and direction of the linear relationship between two variables. However, correlation does not imply causation. Just because two variables are correlated does not mean that one variable causes the other.
There might be other factors that are influencing both variables or the relationship might be coincidental. It’s important to consider other evidence and potential confounding factors before concluding that there is a causal relationship between two variables.
6.4 Ignoring Data Type
The type of data (e.g., continuous, categorical) will influence the choice of appropriate descriptive statistics and comparison techniques. Using inappropriate methods can lead to misleading conclusions.
For example, it’s not appropriate to calculate the mean of categorical data. Instead, you should use frequencies or percentages to describe the distribution of the data.
6.5 Neglecting Statistical Significance
Statistical significance indicates whether the observed differences are likely due to chance or a real effect. However, it’s important to consider the practical significance of the findings as well. A statistically significant difference might not be meaningful in a real-world context.
It’s also important to consider the context of the study and the potential for bias. Statistical significance should not be the only factor considered when drawing conclusions.
6.6 Not Visualizing Data
Visualizing data can greatly enhance understanding and comparison. Ignoring visualization can lead to missed opportunities for identifying patterns, trends, and outliers.
Visualizations can reveal insights that might not be apparent from numerical summaries alone. They are an essential tool for exploring and comparing data.
7. The Future of Descriptive Statistics
Descriptive statistics continue to evolve with advancements in technology and data availability. This section explores emerging trends and future directions.
7.1 Big Data and Descriptive Statistics
The rise of big data has created new opportunities and challenges for descriptive statistics. With vast amounts of data available, it’s more important than ever to be able to summarize and compare data effectively.
Big data also presents new challenges, such as dealing with noisy data, missing values, and computational limitations. New techniques are being developed to address these challenges and to extract meaningful insights from big data.
7.2 Machine Learning and Descriptive Statistics
Machine learning algorithms can be used to automate the process of identifying patterns and trends in data. Descriptive statistics can be used to validate and interpret the results of machine learning models.
Machine learning can also be used to improve the accuracy and efficiency of descriptive statistics calculations. For example, machine learning algorithms can be used to impute missing values or to detect outliers.
7.3 Interactive Data Visualization
Interactive data visualization tools allow users to explore and compare data in real-time. These tools provide a more engaging and intuitive way to understand data than traditional static charts and graphs.
Interactive data visualization tools are becoming increasingly popular in business and research. They allow users to drill down into the data, filter and sort data, and create custom visualizations.
7.4 Cloud-Based Statistical Software
Cloud-based statistical software allows users to access and analyze data from anywhere with an internet connection. This provides greater flexibility and collaboration than traditional desktop-based software.
Cloud-based statistical software is becoming increasingly popular in organizations of all sizes. It offers several advantages, such as scalability, cost-effectiveness, and ease of use.
7.5 Ethical Considerations
As descriptive statistics become more powerful and widely used, it’s important to consider the ethical implications of data analysis. This includes issues such as data privacy, data security, and the potential for bias.
It’s important to use descriptive statistics responsibly and to be transparent about the methods and assumptions used. It’s also important to consider the potential impact of the results on individuals and society.
8. Conclusion: Leveraging Descriptive Statistics for Informed Comparisons
Descriptive statistics provide a powerful toolkit for summarizing and comparing data. By understanding the core concepts, techniques, and potential pitfalls, you can leverage descriptive statistics to make informed decisions across various domains. Remember to choose the right statistical software, visualize your data effectively, and always consider the context of your analysis. For more in-depth comparisons and comprehensive data analysis, visit COMPARE.EDU.VN.
Ready to make data-driven decisions? Visit COMPARE.EDU.VN at 333 Comparison Plaza, Choice City, CA 90210, United States or contact us on Whatsapp at +1 (626) 555-9090. COMPARE.EDU.VN provides detailed and objective comparisons to help you choose the best options for your needs. Explore our website today to discover the power of informed decision-making.
9. Frequently Asked Questions (FAQ)
9.1 What is the difference between descriptive and inferential statistics?
Descriptive statistics summarize the characteristics of a sample, while inferential statistics use sample data to make inferences about a population.
9.2 What are the key measures of central tendency?
The key measures of central tendency are the mean, median, and mode.
9.3 What are the key measures of variability?
The key measures of variability are the range, variance, standard deviation, and interquartile range (IQR).
9.4 How do I choose the right statistical software?
Consider the complexity of the analysis, your programming knowledge, the cost of the software, and the user interface.
9.5 What is skewness and kurtosis?
Skewness measures the asymmetry of a distribution, while kurtosis measures the peakedness of a distribution.
9.6 How do I identify outliers?
Outliers can be identified using box plots or by examining values that are more than 2 or 3 standard deviations away from the mean.
9.7 What is the standard error of the mean?
The standard error of the mean (SEM) measures the precision of the sample mean as an estimate of the population mean.
9.8 What is correlation?
Correlation measures the strength and direction of the linear relationship between two variables.
9.9 What are some common pitfalls to avoid when comparing data?
Common pitfalls include ignoring sample size, overlooking outliers, misinterpreting correlation, ignoring data type, and neglecting statistical significance.
9.10 Where can I find more detailed comparisons and data analysis?
Visit compare.edu.vn for detailed and objective comparisons to help you make informed decisions.