When comparing the effectiveness of different teaching methods or interventions, researchers often focus on statistical significance (p-values). However, a crucial element often overlooked is effect size, which quantifies the magnitude of the difference between groups. This article explores the importance of effect size, particularly in relation to sample size, when comparing teachers or educational interventions.
What is Effect Size and Why is it Important?
Effect size measures the practical significance of a research finding. While a p-value indicates whether a difference is likely due to chance, effect size tells us how large and meaningful that difference actually is. A statistically significant result (small p-value) doesn’t necessarily translate to a large or important effect in real-world classroom settings. When comparing teachers, effect size helps us determine the degree to which one teacher’s approach leads to better student outcomes than another’s.
Can You Compare Teachers Sample Size? The Role of Sample Size in Determining Effect Size
Sample size plays a critical role in the calculation and interpretation of effect size. A larger sample size generally leads to a more precise estimate of the true effect size. With a small sample size, even a large observed difference between groups might not be statistically significant. Conversely, a very large sample size can make even a tiny difference statistically significant, even if that difference is practically insignificant. Therefore, when comparing teachers, a sufficient sample size is crucial to confidently determine if observed differences in student outcomes are truly meaningful.
For instance, if comparing two teachers’ impact on student test scores, a small sample size (e.g., one class each) might not be enough to reliably detect a difference in their effectiveness. A larger sample size (e.g., multiple classes across several years) would provide a more accurate estimate of the true difference in student achievement attributable to each teacher.
Common Effect Size Measures for Comparing Teachers
Several statistical measures can quantify effect size. Some common ones include:
- Cohen’s d: Represents the standardized difference between two means. A d of 0.2 is considered a small effect, 0.5 a medium effect, and 0.8 a large effect. This is often used to compare average student scores between teachers.
- Glass’s Δ (delta): Similar to Cohen’s d but uses the standard deviation of the control group in the denominator, making it useful when comparing to a known baseline or control group.
- Eta squared (η²): Represents the proportion of variance in the outcome variable (e.g., student scores) explained by the grouping variable (e.g., different teachers).
- Odds ratio: Used when comparing the odds of an event occurring in one group versus another (e.g., the odds of a student passing a test with one teacher vs. another). This is useful when comparing categorical outcomes.
Statistical Power and its Relation to Sample Size and Effect Size
Statistical power is the probability of finding a statistically significant effect if a true effect exists. Power is influenced by both effect size and sample size. A larger effect size and a larger sample size both increase statistical power.
Before comparing teachers, researchers should conduct a power analysis to determine the necessary sample size to detect a meaningful effect size with sufficient power. This helps ensure that the study is adequately powered to detect a real difference if one exists. Failing to achieve sufficient power can lead to a Type II error (failing to reject a false null hypothesis), essentially missing a real difference between teaching approaches.
Conclusion
When comparing teachers, considering effect size alongside statistical significance is crucial. Effect size provides a practical measure of the magnitude of differences in student outcomes, while sample size plays a vital role in determining the accuracy and reliability of effect size estimates. By understanding these concepts and conducting appropriate power analyses, researchers can ensure that studies comparing teachers are robust and provide meaningful insights into effective teaching practices.
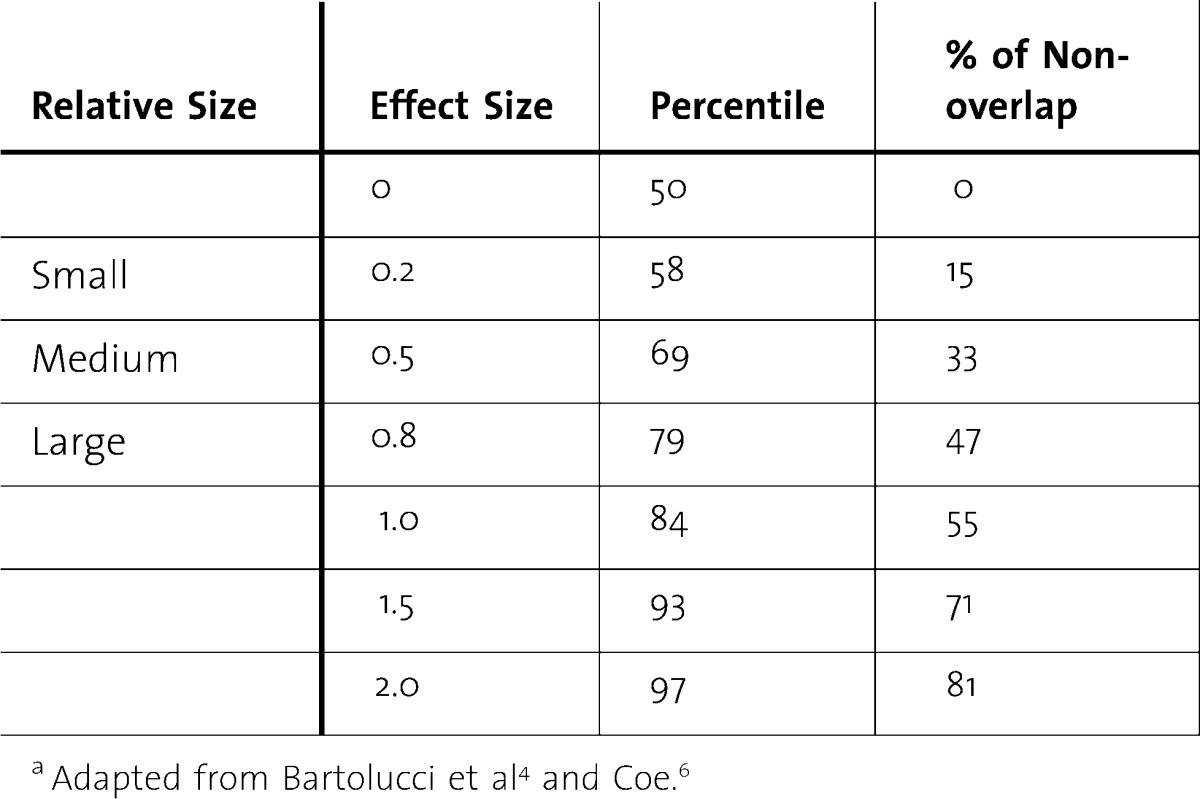alt text: A chart showing the relationship between effect size, sample size, and statistical power.
