T-tests are valuable hypothesis tests in statistics used to compare means. You can use a one-sample t-test to compare a sample mean to a hypothesized value, a two-sample t-test for comparing the means of two groups, and a paired t-test for comparing two groups with paired observations (like before-and-after measurements). But Can You Compare T-values directly? This post delves into t-values, t-distributions, and how t-tests utilize them to calculate probabilities and evaluate hypotheses.
What is a T-Value?
T-tests derive their name from t-values, which are a type of test statistic. A test statistic is a standardized value computed from sample data during a hypothesis test. It compares your data to the expected outcome under the null hypothesis. Each t-test employs a specific formula to distill all your sample data into a single t-value. This calculation considers the difference between your sample mean(s) and the null hypothesis, factoring in both sample size and data variability. A t-value of 0 implies the sample results perfectly match the null hypothesis. The absolute value of the t-value increases as the discrepancy between the sample data and the null hypothesis grows.
A t-value on its own lacks context. For instance, a t-value of 2 doesn’t inherently signify much. To interpret it, we need to understand t-distributions.
Understanding T-Distributions
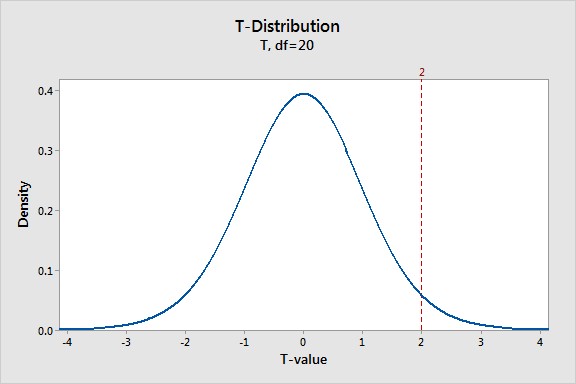
A t-distribution is a probability distribution that represents the distribution of t-values if you were to repeatedly sample from a population where the null hypothesis is true. Each sample size has a corresponding t-distribution defined by its degrees of freedom (DF), which is closely related to the sample size.
The graph above illustrates a t-distribution with 20 degrees of freedom. The peak at zero indicates that obtaining a sample value near the null hypothesis is most probable. As t-values deviate further from zero, their likelihood decreases. This is because t-distributions assume the null hypothesis is true. By placing your study’s t-value within this distribution, you can gauge its consistency with the null hypothesis.
Calculating Probabilities with T-Values and T-Distributions
The core of hypothesis testing involves placing a test statistic within a known probability distribution. In t-tests, calculating the probability associated with a t-value requires placing it within the appropriate t-distribution. This probability, known as the p-value, helps determine the likelihood of observing your sample results (or more extreme results) if the null hypothesis is true. A sufficiently low p-value allows us to reject the null hypothesis.
Calculating the p-value usually involves a two-tailed test, considering both positive and negative t-values. The p-value represents the probability of observing a t-value as extreme as, or more extreme than, the one calculated from your sample data, assuming the null hypothesis is true.
The Impact of Sample Size on T-Distributions
T-distributions are shaped by their degrees of freedom. As degrees of freedom (and consequently, sample size) increase, the t-distribution becomes more concentrated around zero, and the tails become thinner.
Smaller samples have greater uncertainty, resulting in thicker tails in the t-distribution. This reflects the higher probability of observing unusual sample statistics even when the null hypothesis holds true. Consequently, the same t-value can have different p-values depending on the sample size. Larger samples generally lead to more reliable results. While you can’t directly compare t-values from different studies with varying sample sizes, understanding t-distributions helps contextualize these values and interpret the results of t-tests accurately.