Rope tension and weight are fundamental concepts in physics, often encountered in everyday scenarios and engineering applications. Understanding how they relate and differ is crucial for problem-solving in mechanics. This article from COMPARE.EDU.VN will provide a comprehensive comparison of rope tension and weight, exploring their definitions, characteristics, formulas, and practical implications. We aim to clarify the relationship between these forces and equip you with the knowledge to analyze scenarios involving them effectively. Discover the intricacies of force dynamics and load analysis.
1. Defining Tension and Weight
To accurately compare rope tension to weight, we must first define each concept clearly. Tension is the pulling force transmitted axially through a rope, cable, string, or similar object, or by each end of a rod, truss member, or similar object. Weight, on the other hand, is the force exerted on an object due to gravity.
1.1 What is Tension?
Tension is a force that is transmitted through a rope, string, wire, or cable when it is pulled tight by forces acting from opposite ends. This force is directed along the length of the rope and pulls equally on the objects on either end of the rope. In other words, tension is a pulling force acting along a connecting medium, such as a rope or cable. Consider a tug-of-war game; the force exerted on the rope by each team is tension.
- Characteristics of Tension:
- Direction: Always acts along the direction of the rope or cable.
- Nature: It’s a pulling force.
- Transmission: Tension is transmitted equally along the rope if the rope is massless and frictionless pulleys are used.
- Units: Measured in Newtons (N) in the metric system or pounds (lbs) in the imperial system.
1.2 What is Weight?
Weight is the force exerted on an object due to gravity. It is directly proportional to the object’s mass and the local gravitational acceleration. Unlike mass, which is an intrinsic property of an object, weight depends on the gravitational field.
- Characteristics of Weight:
- Direction: Always acts downwards, towards the center of the Earth (or the celestial body exerting the gravitational force).
- Nature: It’s a pulling force due to gravity.
- Dependence: Weight depends on both mass and gravitational acceleration.
- Units: Measured in Newtons (N) in the metric system or pounds (lbs) in the imperial system.
2. Formulas and Calculations
Understanding the formulas associated with tension and weight is essential for solving problems in physics and engineering.
2.1 Calculating Tension
The formula for calculating tension depends on the specific scenario. Here are a few common cases:
- Simple Hanging Mass: If an object of mass m is suspended vertically by a rope, the tension T in the rope is equal to the weight of the object, assuming the rope is not accelerating.
- Formula: T = mg, where g is the acceleration due to gravity (approximately 9.8 m/s² on Earth).
- Horizontal Pull: If a rope is used to pull an object horizontally with an acceleration a, the tension in the rope is given by:
- Formula: T = ma
- Inclined Plane: If an object is on an inclined plane, the tension in the rope supporting the object can be calculated considering the component of weight along the plane.
- System in Equilibrium: In a system where multiple forces are acting, and the system is in equilibrium (i.e., no net force), the tension can be found by balancing all the forces in the system.
2.2 Calculating Weight
The formula for calculating weight is straightforward:
- Formula: W = mg, where:
- W is the weight of the object (in Newtons).
- m is the mass of the object (in kilograms).
- g is the acceleration due to gravity (approximately 9.8 m/s² on Earth).
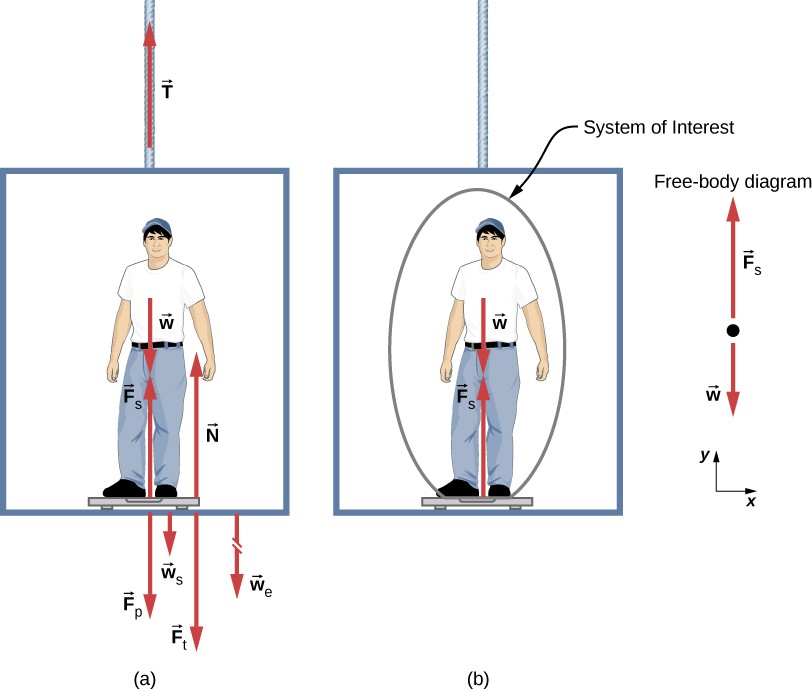Man standing on a scale in an elevator, illustrating forces like tension and weight.
2.3 Example Calculation
Consider a 10 kg object suspended by a rope on Earth.
- Weight Calculation:
- W = mg = 10 kg * 9.8 m/s² = 98 N
- Tension Calculation:
- Since the object is suspended and not accelerating, the tension in the rope T = W = 98 N.
3. Key Differences Between Tension and Weight
While both tension and weight are forces measured in the same units, they arise from different physical phenomena and have distinct characteristics.
3.1 Origin of the Force
- Tension: Arises from the intermolecular forces within a rope or cable when it is pulled tight. It is a response to an external force trying to stretch or elongate the rope.
- Weight: Arises from the gravitational attraction between an object and a celestial body, such as the Earth.
3.2 Direction of the Force
- Tension: Acts along the length of the rope or cable. Its direction is determined by the orientation of the rope and the direction of the pulling forces.
- Weight: Always acts vertically downwards towards the center of the Earth (or the celestial body exerting the gravitational force).
3.3 Dependence on Mass and Gravity
- Tension: Can exist independently of gravity. For example, a rope stretched between two points on a horizontal surface has tension, even though gravity is not directly causing it.
- Weight: Directly depends on both the mass of the object and the gravitational acceleration. If either the mass or the gravitational acceleration changes, the weight will change accordingly.
3.4 Impact of Acceleration
- Tension: Can change significantly depending on the acceleration of the system. For instance, consider an elevator accelerating upwards; the tension in the cable supporting the elevator will be greater than the total weight of the elevator and its contents.
- Weight: While the apparent weight can change due to acceleration (as experienced in an elevator), the actual weight (gravitational force) remains constant as long as the mass and gravitational acceleration do not change.
3.5 Summary Table
| Feature | Tension | Weight |
|---|---|---|
| Origin | Intermolecular forces within a rope/cable when pulled tight | Gravitational attraction between an object and a celestial body |
| Direction | Along the length of the rope/cable | Vertically downwards |
| Dependence | Can exist independently of gravity | Depends on mass and gravitational acceleration |
| Impact of Accel. | Changes significantly with acceleration of the system | Gravitational force remains constant |
| Formula | Varies depending on the scenario (e.g., T = mg, T = ma) | W = mg |
| Example | Force in a rope pulling a sled | Force exerted on a person standing on Earth |
4. Scenarios Where Tension and Weight Interact
Many real-world scenarios involve both tension and weight acting together. Understanding how to analyze these scenarios is crucial for applying the concepts effectively.
4.1 Simple Suspension
- Description: An object is hanging vertically from a rope or cable.
- Analysis: In this case, the tension in the rope is equal to the weight of the object, assuming the system is in equilibrium (i.e., not accelerating). If the object is accelerating upwards or downwards, the tension will be greater or less than the weight, respectively.
4.2 Inclined Plane
- Description: An object is resting on an inclined plane and is supported by a rope.
- Analysis: The weight of the object acts vertically downwards, but only a component of the weight acts along the inclined plane. The tension in the rope must balance this component of the weight, as well as any frictional forces present.
4.3 Elevator Example
- Description: An object (or a person) is standing on a scale inside an elevator.
- Analysis:
- Elevator at Rest or Moving at Constant Velocity: The scale reading (which measures the normal force) is equal to the weight of the object.
- Elevator Accelerating Upwards: The scale reading is greater than the weight of the object because the scale must provide an additional force to accelerate the object upwards.
- Elevator Accelerating Downwards: The scale reading is less than the weight of the object because the scale provides less force than the weight.
Let’s consider the example provided, with a 75.0-kg man standing on a bathroom scale in an elevator.
- (a) Elevator Accelerating Upward at 1.20 m/s²:
- The net force acting on the man is the sum of the scale force ((F_s)) and his weight ((w)).
- Using Newton’s second law: (F_{net} = F_s – w = ma)
- Solving for (F_s): (F_s = ma + w = m(a + g))
- (F_s = (75.0 , text{kg})(1.20 , text{m/s}^2 + 9.80 , text{m/s}^2) = 825 , text{N})
- (b) Elevator Moving Upward at a Constant Speed of 1 m/s:
- Since the elevator moves at a constant speed, the acceleration (a = 0).
- Therefore, (F_s = mg = (75.0 , text{kg})(9.80 , text{m/s}^2) = 735 , text{N})
4.4 Pulley Systems
- Description: A system of pulleys and ropes used to lift or move objects.
- Analysis: Pulleys can change the direction of the tension force and reduce the amount of force needed to lift an object. The tension in the rope and the weight of the object are related by the mechanical advantage of the pulley system.
- Example: A simple pulley system might have a mechanical advantage of 2, meaning that the tension in the rope is half the weight of the object being lifted.
5. Practical Applications
Understanding the relationship between tension and weight is essential in many fields, including engineering, construction, and sports.
5.1 Engineering Design
- Bridges and Buildings: Engineers must carefully calculate the tension in cables and support structures to ensure they can withstand the weight of the bridge or building and any additional loads (e.g., traffic, wind).
- Elevators: As seen in the example above, understanding the tension in elevator cables is crucial for safety. The cables must be strong enough to support the weight of the elevator and its passengers, even during acceleration.
- Cranes: Cranes use cables and pulleys to lift heavy objects. Engineers must calculate the tension in the cables to ensure they do not exceed their maximum load capacity.
5.2 Construction
- Scaffolding: Construction workers use scaffolding to work at heights. The tension in the ropes and cables supporting the scaffolding must be carefully calculated to ensure the safety of the workers.
- Lifting Materials: Construction sites often use cranes or hoists to lift heavy materials. Understanding the tension in the lifting cables is crucial for preventing accidents.
5.3 Sports
- Rock Climbing: Rock climbers rely on ropes to support their weight. The tension in the rope can vary significantly depending on the climber’s position and the angle of the rope.
- Sailing: The tension in the sails and rigging of a sailboat is crucial for controlling the boat’s movement. Sailors must understand how to adjust the tension to optimize performance.
- Zip Lines: Zip lines use cables to allow people to glide from one point to another. The tension in the cable must be strong enough to support the weight of the person and any additional loads.
6. Common Misconceptions
Several common misconceptions exist regarding tension and weight. Addressing these misconceptions can help clarify the concepts.
6.1 Tension is Only in Ropes
- Misconception: Tension only exists in ropes or cables.
- Clarification: Tension can exist in any object that is being pulled or stretched, including rods, beams, and even liquids and gases.
6.2 Weight is the Same as Mass
- Misconception: Weight and mass are the same thing.
- Clarification: Weight is the force exerted on an object due to gravity, while mass is a measure of the amount of matter in an object. Weight depends on gravity, while mass is an intrinsic property of the object.
6.3 Tension is Always Equal to Weight
- Misconception: Tension in a rope is always equal to the weight of the object it is supporting.
- Clarification: Tension is only equal to weight when the object is in equilibrium (i.e., not accelerating). If the object is accelerating, the tension will be different from the weight.
6.4 Zero Tension Means Zero Force
- Misconception: If there’s no tension in a rope, there’s no force acting on it.
- Clarification: Zero tension means the rope is slack and not exerting a pulling force, but other forces like weight or external pushes can still be present.
7. Advanced Concepts
For a deeper understanding of tension and weight, it’s helpful to explore some advanced concepts.
7.1 Stress and Strain
- Stress: The force per unit area acting on a material. It is related to tension in ropes and cables.
- Strain: The deformation of a material caused by stress.
- Relationship: The relationship between stress and strain is described by the material’s Young’s modulus. Understanding stress and strain is crucial for designing structures that can withstand tension forces without breaking or deforming excessively.
7.2 Free Body Diagrams
- Definition: A diagram that shows all the forces acting on an object.
- Application: Free body diagrams are essential for analyzing complex systems involving tension and weight. By drawing a free body diagram, you can identify all the forces acting on the object and apply Newton’s laws to solve for unknown quantities.
7.3 Vector Analysis
- Definition: A mathematical technique for analyzing forces that have both magnitude and direction.
- Application: Tension and weight are vector quantities, meaning they have both magnitude and direction. Vector analysis is crucial for analyzing systems where forces are acting at angles to each other, such as in inclined plane problems.
8. Real-World Examples
Examining real-world examples can help solidify your understanding of tension and weight.
8.1 Suspension Bridges
- Description: Bridges that use cables suspended between towers to support the weight of the bridge deck.
- Analysis: The tension in the cables is enormous and must be carefully calculated to ensure the bridge’s stability. The weight of the bridge deck and any traffic is transferred to the cables, which then transmit the force to the towers.
8.2 Rock Climbing Gear
- Description: Ropes, carabiners, and other gear used by rock climbers.
- Analysis: The tension in the rope can vary significantly depending on the climber’s position and the angle of the rope. The gear must be strong enough to withstand these tension forces without breaking.
8.3 Zip Lines
- Description: Cables used to allow people to glide from one point to another.
- Analysis: The tension in the cable must be strong enough to support the weight of the person and any additional loads (e.g., wind). The angle of the cable and the distance between the supports also affect the tension.
9. Problem-Solving Techniques
Here are some techniques for solving problems involving tension and weight:
- Draw a Free Body Diagram: Identify all the forces acting on the object.
- Apply Newton’s Laws: Use Newton’s first and second laws to relate the forces to the object’s motion.
- Resolve Forces into Components: If the forces are acting at angles to each other, resolve them into horizontal and vertical components.
- Solve the Equations: Solve the resulting equations for the unknown quantities.
- Check Your Answer: Make sure your answer makes sense and has the correct units.
10. Case Studies
Analyzing specific case studies can provide a deeper understanding of how tension and weight interact in real-world scenarios.
10.1 The Tacoma Narrows Bridge Collapse
- Background: The Tacoma Narrows Bridge was a suspension bridge that collapsed in 1940 due to wind-induced vibrations.
- Analysis: The collapse was caused by a phenomenon called aeroelastic flutter, in which the wind interacted with the bridge structure to create oscillating forces. These forces caused the tension in the cables to vary rapidly, eventually leading to the bridge’s collapse.
10.2 Elevator Accidents
- Background: Elevator accidents can occur due to cable failures or other mechanical problems.
- Analysis: Understanding the tension in elevator cables is crucial for preventing accidents. Regular inspections and maintenance are necessary to ensure the cables are strong enough to support the weight of the elevator and its passengers.
10.3 Rock Climbing Accidents
- Background: Rock climbing accidents can occur due to rope failures or other equipment malfunctions.
- Analysis: Climbers must use high-quality ropes and gear and inspect them regularly for wear and tear. Understanding the tension in the rope and the forces acting on the gear is crucial for preventing accidents.
11. Current Research and Developments
Research and development in materials science and engineering continue to improve our understanding and application of tension and weight principles.
11.1 High-Strength Materials
- Development: New materials, such as carbon nanotubes and graphene, are being developed with extremely high tensile strengths.
- Application: These materials could be used to create stronger and lighter cables for bridges, elevators, and other applications.
11.2 Smart Structures
- Development: Structures that can sense and respond to changes in their environment.
- Application: Smart bridges, for example, could monitor the tension in their cables and adjust their support structures to maintain stability.
11.3 Advanced Modeling Techniques
- Development: Computer simulations and finite element analysis are being used to model complex systems involving tension and weight.
- Application: These techniques can help engineers design safer and more efficient structures.
12. Future Trends
Looking ahead, several trends are likely to shape the future of tension and weight applications.
12.1 Lightweight Structures
- Trend: A growing emphasis on creating lightweight structures to reduce energy consumption and improve performance.
- Impact: This trend will drive the development of new materials and designs that can minimize weight while maintaining strength and stability.
12.2 Sustainable Infrastructure
- Trend: A focus on creating sustainable infrastructure that minimizes environmental impact.
- Impact: This trend will lead to the development of new materials and construction techniques that are more environmentally friendly.
12.3 Automation and Robotics
- Trend: Increased use of automation and robotics in construction and maintenance.
- Impact: Robots can be used to inspect and repair structures, reducing the risk to human workers and improving efficiency.
13. FAQ – Can Rope Tension Compare to Weight
-
What is the relationship between tension and weight in a rope supporting a hanging object?
The tension in the rope is equal to the weight of the object if the system is in equilibrium (not accelerating). -
How does acceleration affect the tension in a rope?
If an object is accelerating upwards, the tension in the rope will be greater than the weight of the object. If the object is accelerating downwards, the tension will be less than the weight. -
Can tension exist in a rope even if there is no weight attached to it?
Yes, tension can exist in a rope if it is being pulled tight by forces acting from opposite ends, even if there is no weight attached. -
Is weight the same as mass?
No, weight is the force exerted on an object due to gravity, while mass is a measure of the amount of matter in an object. -
How is tension calculated in a pulley system?
The tension in the rope and the weight of the object are related by the mechanical advantage of the pulley system. The tension is reduced by the factor of the mechanical advantage. -
What are some real-world applications of understanding tension and weight?
Engineering design of bridges and buildings, construction of scaffolding, rock climbing, and sailing are just a few examples. -
What is a free body diagram, and how is it used in analyzing tension and weight?
A free body diagram shows all the forces acting on an object. It is used to identify and analyze the forces, applying Newton’s laws to solve for unknown quantities. -
What is the difference between stress and strain?
Stress is the force per unit area acting on a material, while strain is the deformation of a material caused by stress. -
How do engineers ensure the safety of structures involving tension and weight?
Engineers carefully calculate the tension in cables and support structures, use high-strength materials, and conduct regular inspections and maintenance. -
What are some future trends in the application of tension and weight principles?
Lightweight structures, sustainable infrastructure, and increased use of automation and robotics are some future trends.
14. Conclusion
Understanding the relationship between rope tension and weight is essential for various applications, from simple everyday scenarios to complex engineering designs. While both are forces measured in Newtons or pounds, they originate from different phenomena: tension from intermolecular forces in ropes or cables and weight from gravitational attraction. This article from COMPARE.EDU.VN has provided a detailed comparison, highlighting their differences and interactions. Whether you’re designing a bridge, analyzing a rock climbing scenario, or simply curious about the physics around you, a solid grasp of these concepts is invaluable. By considering the direction, dependence on mass and gravity, and the impact of acceleration, you can effectively analyze and solve problems involving rope tension and weight. For more in-depth comparisons and expert analyses, visit COMPARE.EDU.VN.
Ready to make informed decisions? Explore comprehensive comparisons and expert analyses at COMPARE.EDU.VN. Our detailed reviews help you choose the best options for your needs.
Contact Us:
Address: 333 Comparison Plaza, Choice City, CA 90210, United States
WhatsApp: +1 (626) 555-9090
Website: compare.edu.vn
