Understanding Measurement Invariance in SEM
Comparing results across different groups using Structural Equation Modeling (SEM) is a common practice in research. However, a crucial prerequisite for meaningful comparisons is establishing measurement invariance. This ensures that the construct being measured has the same meaning and structure across the groups being compared. Without measurement invariance, observed differences might reflect differences in how the construct is measured, rather than true differences in the construct itself. This leads to the fundamental question: can I compare SEM results with separate models? The short answer is no, not without first establishing measurement invariance.
What is Measurement Invariance?
Measurement invariance assesses whether a construct is measured equivalently across different groups or over time. If a measure is not invariant, comparing scores across groups becomes problematic, as differences may stem from measurement discrepancies rather than true differences in the underlying construct.
Steps in Testing for Measurement Invariance
Measurement invariance is typically tested using a multi-group confirmatory factor analysis (CFA) approach within SEM. This involves a series of hierarchical tests, each imposing increasingly stringent constraints on the model parameters across groups. The primary steps include:
- Configural Invariance: This initial step examines whether the basic model structure (i.e., the number of factors and the pattern of factor loadings) is the same across groups.
- Metric Invariance (Weak Factorial Invariance): This step tests whether the factor loadings are equal across groups, indicating that the factors measure the construct with the same strength in each group.
- Scalar Invariance (Strong Factorial Invariance): This step examines whether both factor loadings and item intercepts are equal across groups. This ensures that differences in observed scores reflect true differences in the latent factor means.
- Residual Invariance (Strict Factorial Invariance): This final and most stringent step tests for the equality of error variances across groups. While not always required for comparing latent means, it ensures the most comprehensive form of measurement invariance.
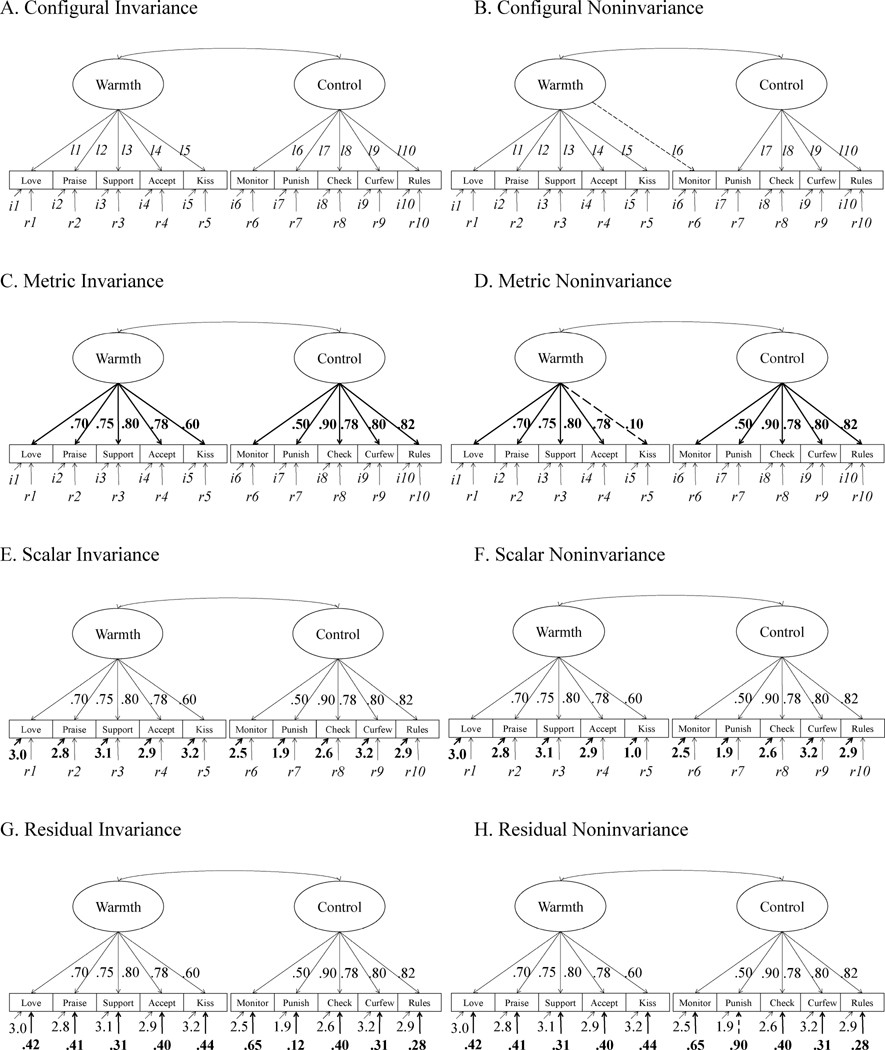Measurement Invariance Steps in SEM
Why You Can’t Compare Separate SEM Models
Comparing results from separate SEM models without testing for measurement invariance is flawed because the scales of the latent variables may differ across groups. This makes it impossible to determine if observed differences are due to true group differences or simply variations in how the construct is measured. Establishing measurement invariance allows researchers to place the latent factors on the same metric, ensuring meaningful comparisons.
Addressing Measurement Non-Invariance
If measurement invariance is not fully supported, researchers have several options:
- Partial Invariance: If only a few parameters are non-invariant, partial invariance may be acceptable. This involves freeing the constraints on the non-invariant parameters while retaining constraints on the others. However, the impact of partial invariance on the interpretation of results needs careful consideration.
- Model Respecification: If substantial non-invariance is detected, researchers might need to revise their model, potentially by removing or modifying items, or exploring alternative factor structures.
- Alternative Analytical Approaches: In cases of severe non-invariance, researchers might consider using alternative analytical techniques that do not rely on the assumption of measurement invariance, such as multi-level modeling or latent class analysis.
Best Practices for Comparing SEM Results
- Always Test for Measurement Invariance: Before comparing SEM results across groups, conduct a series of measurement invariance tests.
- Use Multiple Fit Indices: Rely on a combination of fit indices (e.g., ΔCFI, ΔRMSEA, ΔSRMR) to evaluate model fit and assess measurement invariance.
- Report all Tests and Results: Clearly report the results of all invariance tests, including fit indices, parameter estimates, and decisions regarding model modifications.
- Address Non-Invariance Transparently: If measurement invariance is not fully supported, discuss the implications for the interpretation of results and consider alternative analytical strategies.
Conclusion
Comparing SEM results across groups requires careful attention to measurement invariance. While separate models might seem appropriate, they lack the critical element of a common metric for comparison. By following the outlined steps and best practices, researchers can ensure that their comparisons are valid and meaningful, contributing to a more robust understanding of the phenomena under investigation.
