A single-sample test is a statistical procedure used to determine if there is a significant difference between a sample statistic and a known population parameter. This article will delve into the application of a one-sample t-test to compare the mean height of a sample of college students to the known average height of U.S. adults.
Understanding the One-Sample T-Test
A single-sample test compares a sample statistic, like the mean, to a known population value. The one-sample t-test is specifically designed for scenarios where the population standard deviation is unknown. It helps researchers determine if the observed sample mean is significantly different from the hypothesized population mean. The test calculates a t-statistic, which represents the standardized difference between the sample mean and the population mean.
Case Study: Comparing College Student Height to the U.S. Average
The Centers for Disease Control and Prevention (CDC) reports the average height of U.S. adults aged 20 and older to be approximately 66.5 inches. We will use this as our known population parameter. Our sample consists of 435 students from a single college. We aim to determine if the mean height of these students differs significantly from the national average.
Our hypotheses are:
- Null Hypothesis (H0): The mean height of college students is equal to 66.5 inches (µHeight = 66.5).
- Alternative Hypothesis (H1): The mean height of college students is not equal to 66.5 inches (µHeight ≠ 66.5).
Data Analysis and Visualization
Before conducting the t-test, we analyze the sample data. The ‘Height’ variable, measured in inches, ranges from 55.00 to 88.41.
A histogram visually represents the distribution of student heights. It reveals a relatively symmetrical distribution with a slight right skew. We’ve added two reference lines: one at the sample mean (solid black line) and another at the population mean of 66.5 inches (dashed red line). The sample mean appears slightly higher than the population mean.
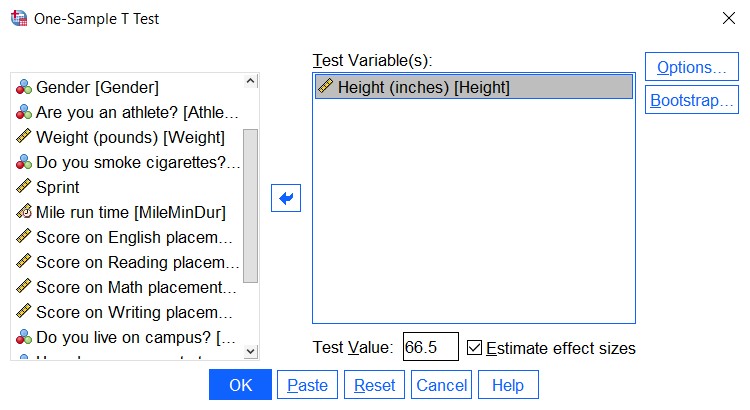
Conducting the One-Sample T-Test in SPSS
We utilize SPSS to perform the one-sample t-test:
- Navigate to Analyze > Compare Means > One-Sample T Test.
- Select the ‘Height’ variable as the Test Variable.
- Input 66.5 in the Test Value field, representing the population mean.
- Click OK.
Interpreting the SPSS Output
The output includes two key sections:
One-Sample Statistics
This table provides descriptive statistics: sample size (n = 408), mean (68.03 inches), standard deviation, and standard error.
One-Sample Test
This table presents the t-statistic (5.810), degrees of freedom (407), p-value (less than 0.001), mean difference (1.53 inches), and the 95% confidence interval for the mean difference (1.013 to 2.050).
Conclusion
The p-value (less than 0.001) is significantly lower than the conventional alpha level of 0.05. This leads us to reject the null hypothesis. A Single-sample Test Compares A Sample Statistic To A Known population value, and in this case, we conclude that there is a statistically significant difference between the mean height of the college students and the national average height for U.S. adults. The data suggests that students at this college are, on average, significantly taller than the general U.S. adult population.