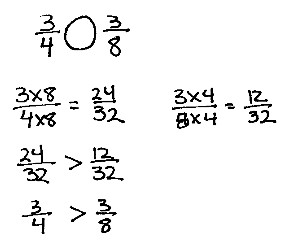Comparing fractions involves determining which fraction represents a larger or smaller part of a whole. While traditional methods like finding common denominators or cross-multiplication exist, understanding the conceptual size of fractions is crucial. This article explores various strategies for comparing fractions, moving beyond rote procedures to develop a deeper understanding of fractional relationships.
Comparing Fractions with Related Denominators
When comparing fractions with related denominators (one denominator is a multiple of the other), like 3/4 and 3/8, we can leverage this relationship for easier comparison. Since 4 is a factor of 8, we can convert 3/4 into eighths. Multiplying both the numerator and denominator of 3/4 by 2, we get 6/8. Now, comparing 6/8 and 3/8 is straightforward: 6/8 is greater than 3/8. Therefore, 3/4 > 3/8.
Comparing Fractions with Common Numerators
Another strategy involves comparing fractions with common numerators, such as 2/3 and 6/8. While the numerators are different here, they are related: 6 is a multiple of 2. To make the numerators the same, we can convert 2/3 into a fraction with a numerator of 6. Multiplying both the numerator and denominator of 2/3 by 3 results in 6/9. Now we compare 6/9 and 6/8. Since ninths are smaller units than eighths, and we have the same number of each unit (6), 6/9 is less than 6/8. Consequently, 2/3 < 6/8.
Utilizing Benchmark Fractions
Benchmark fractions, like 1/2, can be powerful tools for comparison. Consider comparing 3/4 and 3/8 again. We know that 2/4 is equivalent to 1/2, and 3/4 is greater than 2/4. Therefore, 3/4 > 1/2. Similarly, 4/8 is equivalent to 1/2, and 3/8 is less than 4/8. Thus, 3/8 < 1/2. By comparing both fractions to the benchmark of 1/2, we can deduce that 3/4 > 3/8.
Reasoning with Distance from One
When neither numerators nor denominators are related, as in the case of 2/3 and 7/8, we can compare their distance from 1. The fraction 2/3 is 1/3 away from 1, while 7/8 is 1/8 away from 1. Since thirds are larger units than eighths, 1/3 represents a greater distance than 1/8. Therefore, 2/3 is further from 1 than 7/8, meaning 2/3 < 7/8.
Conclusion
Comparing fractions is more than just applying procedures; it’s about understanding the relative sizes of fractions. Utilizing strategies based on related denominators, common numerators, benchmark fractions, and distance from one allows for deeper comprehension and flexible problem-solving. These strategies empower students to reason about fractional quantities and develop a more robust understanding of number sense.