Comparing different fractions can seem tricky, but it’s a fundamental skill in mathematics and essential for various real-life applications. At COMPARE.EDU.VN, we offer comprehensive guides and tools to simplify this process, providing clarity and confidence in your comparisons. By understanding the various methods and rules, you can easily determine which fraction is larger, smaller, or if they are equivalent.
1. Understanding the Basics of Fractions
Before diving into the comparison methods, it’s crucial to understand what a fraction represents. A fraction is a part of a whole, expressed as a numerator and a denominator. The numerator represents the number of parts you have, while the denominator represents the total number of equal parts the whole is divided into. For instance, in the fraction 3/4, 3 is the numerator, and 4 is the denominator, indicating that you have 3 parts out of a total of 4. Grasping this concept lays the groundwork for effectively comparing different fractions.
1.1 What is a Fraction?
A fraction represents a part of a whole. It’s written as a ratio of two numbers, the numerator and the denominator, separated by a fraction bar. The numerator is the number above the bar, indicating how many parts of the whole are being considered. The denominator is the number below the bar, indicating the total number of equal parts that make up the whole.
For example, in the fraction ½, the numerator is 1 and the denominator is 2. This means one part out of two equal parts is being considered. Understanding this fundamental concept is crucial before comparing fractions.
1.2 Types of Fractions
Fractions come in different forms, each with its own characteristics:
- Proper Fractions: The numerator is less than the denominator (e.g., 2/5).
- Improper Fractions: The numerator is greater than or equal to the denominator (e.g., 7/3).
- Mixed Numbers: A whole number combined with a proper fraction (e.g., 2 1/4).
1.3 Why is Comparing Fractions Important?
Comparing fractions isn’t just an academic exercise; it’s a practical skill used in everyday situations. Whether you’re adjusting a recipe, measuring ingredients, or analyzing data, knowing how to compare fractions accurately is essential.
2. Comparing Fractions with Like Denominators
The simplest scenario for comparing fractions is when they share the same denominator. When fractions have the same denominator, the fraction with the larger numerator is the larger fraction. This is because the denominator represents the size of each part, and when that size is the same, you only need to compare the number of parts. For example, comparing 3/7 and 5/7, since 5 is greater than 3, 5/7 is the larger fraction. This method provides a straightforward way to compare fractions when the denominators are identical.
2.1 The Rule for Like Denominators
When fractions have the same denominator, the fraction with the larger numerator is the larger fraction. The denominator indicates the size of each part, so when the denominators are the same, the comparison comes down to the number of parts.
For example:
- 3/5 and 4/5
- Since 4 > 3, then 4/5 > 3/5
2.2 Examples of Comparing Like Fractions
Let’s look at a few examples:
-
Compare 2/9 and 7/9:
- Both fractions have the same denominator (9).
- Compare the numerators: 2 and 7.
- Since 7 > 2, then 7/9 > 2/9.
-
Compare 5/11 and 1/11:
- Both fractions have the same denominator (11).
- Compare the numerators: 5 and 1.
- Since 5 > 1, then 5/11 > 1/11.
2.3 Practice Problems
Try these practice problems to reinforce your understanding:
- Which is larger: 8/15 or 4/15?
- Which is smaller: 3/7 or 6/7?
- Are 9/10 and 5/10 equal?
3. Comparing Fractions with Unlike Denominators
When fractions have different denominators, you can’t directly compare their numerators. Instead, you need to find a common denominator, which is a shared multiple of both denominators. The least common denominator (LCD) is the smallest number that both denominators divide into evenly. Once you’ve converted the fractions to have the same denominator, you can compare the numerators as described above. This method ensures an accurate comparison by expressing both fractions in terms of the same-sized parts.
3.1 Finding a Common Denominator
To compare fractions with different denominators, the first step is to find a common denominator. This is a number that is a multiple of both denominators.
For example, if you want to compare 1/3 and 1/4:
- The multiples of 3 are: 3, 6, 9, 12, 15, …
- The multiples of 4 are: 4, 8, 12, 16, 20, …
- The smallest common multiple is 12, so 12 is the common denominator.
3.2 Using the Least Common Multiple (LCM)
The Least Common Multiple (LCM) is the smallest number that is a multiple of both denominators. Using the LCM as the common denominator simplifies the fractions and makes the comparison easier.
To find the LCM:
- List the multiples of each denominator.
- Identify the smallest multiple that both lists share.
For example:
- To compare 1/6 and 3/8, find the LCM of 6 and 8.
- Multiples of 6: 6, 12, 18, 24, 30, …
- Multiples of 8: 8, 16, 24, 32, 40, …
- The LCM is 24.
3.3 Converting Fractions to Equivalent Forms
Once you’ve found the common denominator, you need to convert each fraction into an equivalent fraction with that denominator. To do this, multiply both the numerator and the denominator of each fraction by the number that, when multiplied by the original denominator, equals the common denominator.
For example:
- Compare 1/3 and 1/4 using the common denominator 12.
- For 1/3, multiply both the numerator and denominator by 4: (1 4) / (3 4) = 4/12
- For 1/4, multiply both the numerator and denominator by 3: (1 3) / (4 3) = 3/12
3.4 Examples of Comparing Unlike Fractions
-
Compare 2/5 and 3/7:
- Find the LCM of 5 and 7: LCM(5, 7) = 35
- Convert 2/5 to an equivalent fraction with a denominator of 35: (2 7) / (5 7) = 14/35
- Convert 3/7 to an equivalent fraction with a denominator of 35: (3 5) / (7 5) = 15/35
- Compare the numerators: 14 and 15
- Since 15 > 14, then 15/35 > 14/35, so 3/7 > 2/5.
-
Compare 1/4 and 2/9:
- Find the LCM of 4 and 9: LCM(4, 9) = 36
- Convert 1/4 to an equivalent fraction with a denominator of 36: (1 9) / (4 9) = 9/36
- Convert 2/9 to an equivalent fraction with a denominator of 36: (2 4) / (9 4) = 8/36
- Compare the numerators: 9 and 8
- Since 9 > 8, then 9/36 > 8/36, so 1/4 > 2/9.
4. Decimal Method of Comparing Fractions
Another effective method for comparing fractions involves converting them to decimal form. To convert a fraction to a decimal, divide the numerator by the denominator. Once you have the decimal equivalents, you can easily compare the values. For instance, to compare 1/4 and 1/5, convert them to decimals: 1/4 = 0.25 and 1/5 = 0.20. Since 0.25 is greater than 0.20, 1/4 is the larger fraction. This method is particularly useful when dealing with fractions that are not easily converted to a common denominator.
4.1 Converting Fractions to Decimals
To convert a fraction to a decimal, divide the numerator by the denominator. This process transforms the fraction into a decimal number, which can then be easily compared.
For example:
- To convert 3/4 to a decimal, divide 3 by 4: 3 ÷ 4 = 0.75
- To convert 1/5 to a decimal, divide 1 by 5: 1 ÷ 5 = 0.2
4.2 Comparing Decimal Values
Once the fractions are converted to decimals, compare their values as you would with any decimal numbers. Look at the whole number part first, then move to the tenths place, hundredths place, and so on, until you find a difference.
For example:
- Compare 0.75 and 0.2
-
- 75 has 7 tenths, while 0.2 has 2 tenths.
- Since 7 > 2, then 0.75 > 0.2
4.3 Examples Using the Decimal Method
-
Compare 3/8 and 5/16:
- Convert 3/8 to a decimal: 3 ÷ 8 = 0.375
- Convert 5/16 to a decimal: 5 ÷ 16 = 0.3125
- Compare the decimals: 0.375 and 0.3125
- Since 0.375 > 0.3125, then 3/8 > 5/16.
-
Compare 1/3 and 2/7:
- Convert 1/3 to a decimal: 1 ÷ 3 = 0.333…
- Convert 2/7 to a decimal: 2 ÷ 7 = 0.2857…
- Compare the decimals: 0.333… and 0.2857…
- Since 0.333… > 0.2857…, then 1/3 > 2/7.
4.4 Advantages and Disadvantages
- Advantages:
- Simple and straightforward.
- Works well for any pair of fractions.
- Disadvantages:
- May require long division for some fractions.
- Some decimals are repeating, which may require rounding.
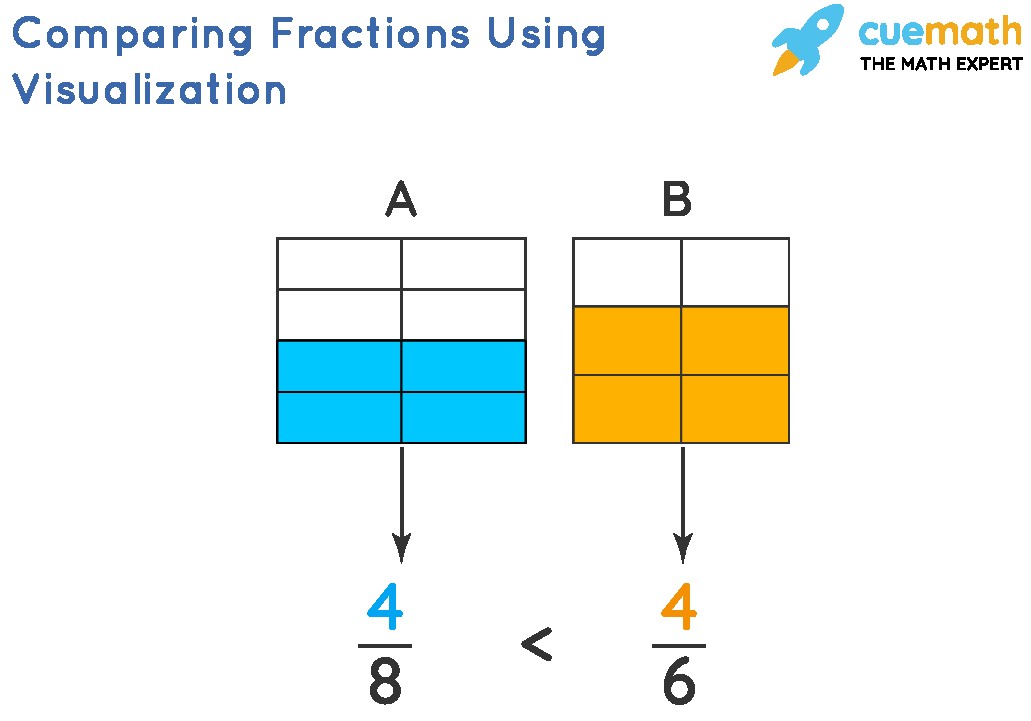
5. Comparing Fractions Using Visualization
Visual methods provide an intuitive way to compare fractions, especially for those who are visually oriented. One common technique is to use area models, such as rectangles or circles, to represent the whole. Divide each model into the number of parts indicated by the denominator, and shade the number of parts indicated by the numerator. By visually comparing the shaded areas, you can easily determine which fraction represents a larger portion of the whole. This method is particularly helpful for understanding the relative sizes of fractions.
5.1 Using Area Models
Area models are visual representations that help compare fractions by showing the proportional areas they represent. These models often use shapes like rectangles or circles to represent the whole.
To use area models:
- Draw two identical shapes (e.g., rectangles or circles).
- Divide each shape into the number of parts indicated by the denominator of each fraction.
- Shade the number of parts indicated by the numerator of each fraction.
- Visually compare the shaded areas to determine which fraction is larger.
5.2 Examples of Visual Comparisons
-
Compare 1/2 and 3/4:
- Draw two identical rectangles.
- Divide the first rectangle into 2 equal parts and shade 1 part (1/2).
- Divide the second rectangle into 4 equal parts and shade 3 parts (3/4).
- By visually comparing the shaded areas, you can see that 3/4 is larger than 1/2.
-
Compare 2/3 and 1/6:
- Draw two identical circles.
- Divide the first circle into 3 equal parts and shade 2 parts (2/3).
- Divide the second circle into 6 equal parts and shade 1 part (1/6).
- By visually comparing the shaded areas, you can see that 2/3 is larger than 1/6.
5.3 Benefits of Visual Methods
- Intuitive Understanding: Visual methods provide a concrete way to understand the size of fractions.
- Easy for Beginners: Ideal for introducing fraction concepts to learners.
- No Calculations Required: Avoids the need for complex calculations.
6. Comparing Fractions Using Cross Multiplication
Cross multiplication is a quick and efficient method for comparing two fractions. To use this method, multiply the numerator of the first fraction by the denominator of the second fraction, and then multiply the numerator of the second fraction by the denominator of the first fraction. Compare the two products. If the first product is larger, then the first fraction is larger. If the second product is larger, then the second fraction is larger. If the products are equal, the fractions are equivalent. This method bypasses the need to find a common denominator, making it a convenient tool for quick comparisons.
6.1 The Cross Multiplication Technique
Cross multiplication involves multiplying the numerator of one fraction by the denominator of the other fraction and comparing the resulting products.
To compare fractions a/b and c/d:
- Multiply the numerator of the first fraction (a) by the denominator of the second fraction (d): a * d
- Multiply the numerator of the second fraction (c) by the denominator of the first fraction (b): c * b
- Compare the products:
- If a d > c b, then a/b > c/d
- If a d < c b, then a/b < c/d
- If a d = c b, then a/b = c/d
6.2 Examples of Cross Multiplication
-
Compare 2/3 and 3/4:
- Multiply 2 (numerator of the first fraction) by 4 (denominator of the second fraction): 2 * 4 = 8
- Multiply 3 (numerator of the second fraction) by 3 (denominator of the first fraction): 3 * 3 = 9
- Compare the products: 8 and 9
- Since 9 > 8, then 3/4 > 2/3.
-
Compare 1/5 and 2/9:
- Multiply 1 by 9: 1 * 9 = 9
- Multiply 2 by 5: 2 * 5 = 10
- Compare the products: 9 and 10
- Since 10 > 9, then 2/9 > 1/5.
6.3 Advantages of Cross Multiplication
- Quick and Efficient: Provides a fast way to compare fractions without finding a common denominator.
- Simple to Use: Easy to remember and apply, making it ideal for quick comparisons.
- No Need for LCM: Bypasses the need to calculate the least common multiple.
7. Real-World Applications of Comparing Fractions
Comparing fractions isn’t just a theoretical exercise; it’s a practical skill that applies to many real-world situations. Whether you’re cooking, managing finances, or analyzing data, the ability to compare fractions accurately can help you make informed decisions. Understanding these applications underscores the importance of mastering fraction comparison techniques.
7.1 Cooking and Baking
In cooking and baking, recipes often call for fractional amounts of ingredients. Comparing fractions helps you adjust recipes, measure ingredients accurately, and ensure the final dish turns out as expected.
- Example: A recipe calls for 2/3 cup of flour and 1/2 cup of sugar. To determine which ingredient is needed in a larger quantity, you need to compare 2/3 and 1/2.
7.2 Financial Planning
When managing finances, you may need to compare fractions to understand proportions of expenses, investments, or savings. This helps you make informed decisions about budgeting and resource allocation.
- Example: You allocate 1/4 of your income to rent and 1/5 to transportation. Comparing 1/4 and 1/5 helps you see which expense takes a larger portion of your income.
7.3 Measuring and Construction
In fields like construction and engineering, accurate measurements are crucial. Comparing fractions is essential for cutting materials to the right size, calculating dimensions, and ensuring structures are built according to specifications.
- Example: A piece of wood needs to be cut to 3/8 of a meter, and another to 1/3 of a meter. Comparing 3/8 and 1/3 helps you determine which piece is longer.
7.4 Data Analysis
In data analysis, fractions are often used to represent proportions and percentages. Comparing fractions helps you interpret data, identify trends, and draw meaningful conclusions.
- Example: A survey shows that 3/5 of respondents prefer option A, while 2/7 prefer option B. Comparing 3/5 and 2/7 helps you determine which option is more popular.
8. Tips and Tricks for Quick Comparisons
Comparing fractions can be made easier with a few handy tips and tricks. These strategies can help you quickly assess the relative sizes of fractions without performing detailed calculations. Mastering these shortcuts can save time and improve your accuracy in various situations.
8.1 Benchmarking
Benchmarking involves comparing fractions to common reference points like 0, 1/2, and 1. This technique helps you quickly assess the relative size of a fraction without performing precise calculations.
- Comparing to 0: Any proper fraction is greater than 0.
- Comparing to 1/2: If the numerator is more than half the denominator, the fraction is greater than 1/2; otherwise, it is less than 1/2.
- Comparing to 1: Any proper fraction is less than 1, while any improper fraction is greater than 1.
For example:
- 3/8 is less than 1/2 because 3 is less than half of 8.
- 5/9 is greater than 1/2 because 5 is more than half of 9.
8.2 Comparing to One
Comparing fractions to one can quickly determine if a fraction is greater or less than a whole unit.
- If the numerator is less than the denominator, the fraction is less than one (a proper fraction).
- If the numerator is equal to the denominator, the fraction is equal to one.
- If the numerator is greater than the denominator, the fraction is greater than one (an improper fraction).
For example:
- 4/5 is less than 1 because 4 < 5.
- 7/7 is equal to 1 because 7 = 7.
- 9/7 is greater than 1 because 9 > 7.
8.3 Using Common Equivalents
Familiarize yourself with common fraction equivalents, such as:
- 1/4 = 25% = 0.25
- 1/3 = 33.33% = 0.333…
- 1/2 = 50% = 0.5
- 2/3 = 66.66% = 0.666…
- 3/4 = 75% = 0.75
Knowing these equivalents can help you quickly compare fractions without detailed calculations.
8.4 Estimating and Approximating
Estimating and approximating can help you quickly compare fractions, especially when precise calculations are not necessary. Round the fractions to the nearest benchmark (0, 1/2, or 1) and compare the rounded values.
For example:
- To compare 7/15 and 9/16:
- 7/15 is approximately 1/2.
- 9/16 is slightly more than 1/2.
- Therefore, 9/16 is slightly larger than 7/15.
9. Common Mistakes to Avoid When Comparing Fractions
When comparing fractions, it’s easy to make mistakes that can lead to incorrect conclusions. Being aware of these common pitfalls can help you avoid them and ensure accurate comparisons. Let’s explore some frequent errors and how to steer clear of them.
9.1 Ignoring the Denominator
A common mistake is to focus solely on the numerator when comparing fractions with different denominators. The denominator is crucial because it indicates the size of the parts. For example, mistaking 1/5 for being larger than 1/2 just because 5 is greater than 2 is a typical error. Always consider the denominator to understand the size of the parts before comparing the numerators.
9.2 Incorrectly Applying Cross Multiplication
Cross multiplication is a handy shortcut, but it must be applied correctly. Ensure you multiply the numerator of the first fraction by the denominator of the second fraction and vice versa. Mixing up the multiplication order can lead to incorrect comparisons. Always double-check your multiplication to avoid this mistake.
9.3 Not Finding a Common Denominator
When comparing fractions with unlike denominators, failing to find a common denominator is a significant error. You cannot accurately compare fractions unless they are expressed in terms of the same-sized parts. Always find the least common multiple (LCM) of the denominators and convert the fractions accordingly before comparing.
9.4 Misunderstanding Mixed Numbers
Mixed numbers combine whole numbers and fractions, and they require special attention when comparing. Before comparing, convert mixed numbers to improper fractions or compare the whole number parts first. For example, compare 2 1/4 and 1 3/4 by either converting them to improper fractions (9/4 and 7/4) or noting that 2 1/4 is greater because 2 > 1.
9.5 Relying Solely on Visual Estimation
While visual methods can be helpful, relying solely on visual estimation without any calculation can be misleading. Visual representations might not always be precise, especially with fractions that are close in value. Use visual aids as a starting point, but always verify with calculations to ensure accuracy.
10. Practice Problems and Solutions
To solidify your understanding of comparing fractions, let’s work through some practice problems with detailed solutions. These exercises cover a range of scenarios, including like denominators, unlike denominators, and different comparison methods, ensuring you’re well-prepared to tackle any fraction comparison challenge.
10.1 Problem Set 1: Comparing Like Fractions
-
Problem: Which is larger: 3/11 or 7/11?
- Solution: Both fractions have the same denominator (11). Compare the numerators: 3 and 7. Since 7 > 3, then 7/11 > 3/11.
-
Problem: Which is smaller: 5/9 or 2/9?
- Solution: Both fractions have the same denominator (9). Compare the numerators: 5 and 2. Since 2 < 5, then 2/9 < 5/9.
-
Problem: Are 4/7 and 4/7 equal?
- Solution: Both fractions are identical: 4/7 = 4/7.
10.2 Problem Set 2: Comparing Unlike Fractions
-
Problem: Which is larger: 2/5 or 3/8?
- Solution: Find the LCM of 5 and 8: LCM(5, 8) = 40. Convert 2/5 to an equivalent fraction with a denominator of 40: (2 8) / (5 8) = 16/40. Convert 3/8 to an equivalent fraction with a denominator of 40: (3 5) / (8 5) = 15/40. Compare the numerators: 16 and 15. Since 16 > 15, then 2/5 > 3/8.
-
Problem: Which is smaller: 1/3 or 2/7?
- Solution: Find the LCM of 3 and 7: LCM(3, 7) = 21. Convert 1/3 to an equivalent fraction with a denominator of 21: (1 7) / (3 7) = 7/21. Convert 2/7 to an equivalent fraction with a denominator of 21: (2 3) / (7 3) = 6/21. Compare the numerators: 7 and 6. Since 6 < 7, then 2/7 < 1/3.
-
Problem: Are 3/4 and 9/12 equal?
- Solution: Find the LCM of 4 and 12: LCM(4, 12) = 12. Convert 3/4 to an equivalent fraction with a denominator of 12: (3 3) / (4 3) = 9/12. Compare the fractions: 9/12 = 9/12. Therefore, 3/4 = 9/12.
10.3 Problem Set 3: Using the Decimal Method
-
Problem: Which is larger: 5/8 or 7/12?
- Solution: Convert 5/8 to a decimal: 5 ÷ 8 = 0.625. Convert 7/12 to a decimal: 7 ÷ 12 = 0.5833…. Compare the decimals: 0.625 > 0.5833…. Therefore, 5/8 > 7/12.
-
Problem: Which is smaller: 2/3 or 5/9?
- Solution: Convert 2/3 to a decimal: 2 ÷ 3 = 0.666…. Convert 5/9 to a decimal: 5 ÷ 9 = 0.555…. Compare the decimals: 0.555… < 0.666…. Therefore, 5/9 < 2/3.
-
Problem: Are 1/4 and 3/12 equal?
- Solution: Convert 1/4 to a decimal: 1 ÷ 4 = 0.25. Convert 3/12 to a decimal: 3 ÷ 12 = 0.25. Compare the decimals: 0.25 = 0.25. Therefore, 1/4 = 3/12.
11. Frequently Asked Questions (FAQs) About Comparing Fractions
To further clarify any lingering questions, here’s a comprehensive FAQ section addressing common concerns and queries related to comparing fractions.
11.1 What does Comparing Fractions Mean?
Comparing fractions means determining which of two or more fractions is larger, smaller, or if they are equal in value. This involves using different methods to assess the relative size of the fractions.
11.2 How do you Compare Fractions with the Same Denominator?
When fractions have the same denominator, the fraction with the larger numerator is the larger fraction. For example, 5/7 > 3/7 because 5 > 3.
11.3 What is the Rule when Comparing Fractions with the Same Numerator?
When fractions have the same numerator, the fraction with the smaller denominator is larger. For example, 1/3 > 1/5 because 3 < 5.
11.4 What are Equivalent Fractions?
Equivalent fractions are fractions that have different numerators and denominators but represent the same value. For example, 1/2 and 2/4 are equivalent fractions because they both equal 0.5.
11.5 What is the Easiest Way of Comparing Fractions?
The easiest way to compare fractions often depends on the specific fractions being compared. For fractions with like denominators, simply compare the numerators. For unlike denominators, converting to decimals or using cross multiplication can be the quickest methods.
11.6 Why do we Need to Compare Fractions?
Comparing fractions is essential for various real-life applications, such as cooking, financial planning, measuring, and data analysis. It helps in making informed decisions and accurate calculations in these areas.
11.7 How to Compare Fractions with Different Denominators?
To compare fractions with different denominators, find the least common multiple (LCM) of the denominators, convert the fractions to equivalent fractions with the LCM as the denominator, and then compare the numerators.
12. Conclusion: Mastering the Art of Comparing Fractions
Mastering the art of comparing fractions is a valuable skill that extends far beyond the classroom. By understanding the various methods and techniques, you can confidently tackle fraction comparisons in any situation. From cooking and baking to financial planning and data analysis, the ability to accurately compare fractions empowers you to make informed decisions and precise calculations. Remember, practice makes perfect, so keep honing your skills and exploring new challenges.
Ready to put your fraction comparison skills to the test? Visit COMPARE.EDU.VN for more resources, practice problems, and interactive tools to help you excel in mathematics and real-life applications. Our platform offers comprehensive guides and expert insights to simplify complex concepts and empower you to make confident decisions. Contact us today at 333 Comparison Plaza, Choice City, CA 90210, United States. Whatsapp: +1 (626) 555-9090. Visit our website at compare.edu.vn to discover more!