Comparing fractions can seem tricky, but it’s a fundamental skill with real-world applications, and COMPARE.EDU.VN is here to simplify the process. Understanding How We Compare Fractions, including equivalent fractions and fraction comparison methods, allows you to determine which fraction represents a larger or smaller portion of a whole. Explore different fraction comparison strategies and comparing fractional values to master comparing fractions with confidence.
Are you struggling to compare fractions? COMPARE.EDU.VN offers a comprehensive guide to make fraction comparison easier. From understanding equivalent fractions to mastering different comparison methods, we provide the tools and knowledge you need to confidently determine the larger or smaller fractional value. Dive in to master the fraction comparison strategies!
1. Understanding the Basics of Fractions
Before diving into comparison methods, it’s crucial to grasp the fundamentals of what a fraction represents. A fraction is a numerical representation of a part of a whole. It is written as two numbers separated by a line: a numerator (the top number) and a denominator (the bottom number).
- Numerator: Indicates the number of parts we are considering.
- Denominator: Indicates the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we are considering 3 parts out of a total of 4 equal parts.
1.1. Types of Fractions
Understanding the different types of fractions is also essential for effective comparison. Here are the main categories:
- Proper Fractions: The numerator is less than the denominator (e.g., 2/5, 7/8).
- Improper Fractions: The numerator is greater than or equal to the denominator (e.g., 5/2, 8/8).
- Mixed Numbers: A whole number combined with a proper fraction (e.g., 1 1/2, 3 1/4).
- Equivalent Fractions: Fractions that represent the same value, even though they have different numerators and denominators (e.g., 1/2 and 2/4).
1.2. Why is Comparing Fractions Important?
Comparing fractions is not just a mathematical exercise; it’s a skill that’s applicable in numerous real-life scenarios. Here are a few examples:
- Cooking: Adjusting recipes to serve different numbers of people often involves comparing fractional amounts of ingredients.
- Construction: Measuring and cutting materials to the correct proportions relies on understanding fractional units.
- Finance: Comparing investment returns or interest rates often involves comparing fractions or percentages.
- Time Management: Allocating time to different tasks often involves dividing your day into fractional segments.
- Academic Performance: Understanding your test scores to see if you are performing at the same level compared to your peers.
2. Comparing Fractions with the Same Denominator: A Simple Start
The easiest scenario for comparing fractions is when they share the same denominator. When the denominators are identical, the fraction with the larger numerator is the larger fraction.
Rule: If a/c and b/c are two fractions with the same denominator c, then:
- If a > b, then a/c > b/c
- If a < b, then a/c < b/c
- If a = b, then a/c = b/c
Example:
Compare 3/8 and 5/8.
Both fractions have a denominator of 8. Comparing the numerators, we see that 5 is greater than 3. Therefore, 5/8 is greater than 3/8.
Alt Text: Visual representation of comparing fractions with the same denominator, showing 3/8 and 5/8.
2.1. Practical Examples
Let’s look at some real-world examples to solidify this concept:
- Pizza Slices: Imagine you have a pizza cut into 6 slices. You eat 2 slices (2/6), and your friend eats 3 slices (3/6). Your friend ate more pizza because 3/6 > 2/6.
- Class Participation: In a class of 20 students, 7 participate actively (7/20) in Group A and 9 participate actively (9/20) in Group B. Group B has more participants because 9/20 > 7/20.
- Time Allocation: If you spend 1/4 of your day studying and 2/4 of your day working, you spend more time working because 2/4 > 1/4.
3. Comparing Fractions with Different Denominators: Finding Common Ground
When fractions have different denominators, the comparison requires an extra step. The key is to find a common denominator, allowing you to compare the numerators directly.
3.1. Finding the Least Common Denominator (LCD)
The most efficient way to find a common denominator is to determine the Least Common Multiple (LCM) of the denominators. The LCM is the smallest number that is a multiple of both denominators. This LCM becomes the Least Common Denominator (LCD).
Steps to Find the LCD:
- List the multiples of each denominator.
- Identify the smallest multiple that appears in both lists.
Example:
Find the LCD of 1/4 and 1/6.
- Multiples of 4: 4, 8, 12, 16, 20, 24…
- Multiples of 6: 6, 12, 18, 24, 30…
The smallest multiple that appears in both lists is 12. Therefore, the LCD is 12.
3.2. Converting Fractions to Equivalent Fractions with the LCD
Once you’ve found the LCD, convert each fraction into an equivalent fraction with the LCD as the new denominator.
Steps to Convert:
- Divide the LCD by the original denominator.
- Multiply both the numerator and the denominator of the original fraction by the result from step 1.
Example:
Convert 1/4 and 1/6 to equivalent fractions with a denominator of 12.
- For 1/4: 12 ÷ 4 = 3. Multiply both the numerator and denominator by 3: (1 3) / (4 3) = 3/12.
- For 1/6: 12 ÷ 6 = 2. Multiply both the numerator and denominator by 2: (1 2) / (6 2) = 2/12.
Now you can easily compare 3/12 and 2/12. Since 3 > 2, 3/12 > 2/12, which means 1/4 > 1/6.
3.3. Alternative Method: Cross-Multiplication
Cross-multiplication is a quick method to compare two fractions without explicitly finding the LCD.
Steps:
- Multiply the numerator of the first fraction by the denominator of the second fraction.
- Multiply the numerator of the second fraction by the denominator of the first fraction.
- Compare the two products.
Example:
Compare 2/5 and 3/7 using cross-multiplication.
- 2 * 7 = 14
- 3 * 5 = 15
Since 15 > 14, 3/7 > 2/5.
Alt Text: Illustration of cross-multiplication method for comparing fractions, showing 2/5 and 3/7.
4. Comparing Mixed Numbers: A Two-Step Approach
Mixed numbers combine a whole number and a fraction. To compare them, follow these steps:
- Compare the Whole Numbers: If the whole numbers are different, the mixed number with the larger whole number is the larger number.
- If the Whole Numbers are the Same: Compare the fractional parts using the methods described earlier (common denominator or cross-multiplication).
Example:
Compare 2 1/3 and 2 3/4.
The whole numbers are the same (both are 2). Now compare the fractional parts: 1/3 and 3/4.
Using cross-multiplication:
- 1 * 4 = 4
- 3 * 3 = 9
Since 9 > 4, 3/4 > 1/3. Therefore, 2 3/4 > 2 1/3.
4.1. Converting Mixed Numbers to Improper Fractions
An alternative approach is to convert mixed numbers to improper fractions and then compare the improper fractions.
Steps to Convert:
- Multiply the whole number by the denominator of the fraction.
- Add the numerator to the result.
- Place the sum over the original denominator.
Example:
Convert 2 1/3 to an improper fraction:
- 2 * 3 = 6
- 6 + 1 = 7
- The improper fraction is 7/3.
Now, convert 2 3/4 to an improper fraction:
- 2 * 4 = 8
- 8 + 3 = 11
- The improper fraction is 11/4.
Now you can compare 7/3 and 11/4 using common denominators or cross-multiplication.
5. Using Decimals to Compare Fractions: A Different Perspective
Converting fractions to decimals provides another way to compare their values. This method is particularly useful when dealing with complex fractions or when a calculator is readily available.
5.1. Converting Fractions to Decimals
To convert a fraction to a decimal, simply divide the numerator by the denominator.
Example:
Convert 3/8 to a decimal:
3 ÷ 8 = 0.375
Convert 5/8 to a decimal:
5 ÷ 8 = 0.625
Now you can easily compare 0.375 and 0.625. Since 0.625 > 0.375, 5/8 > 3/8.
5.2. Advantages and Disadvantages
- Advantage: Decimals are easy to compare, especially when using a calculator.
- Disadvantage: Some fractions result in repeating decimals, which may require rounding and introduce a slight inaccuracy.
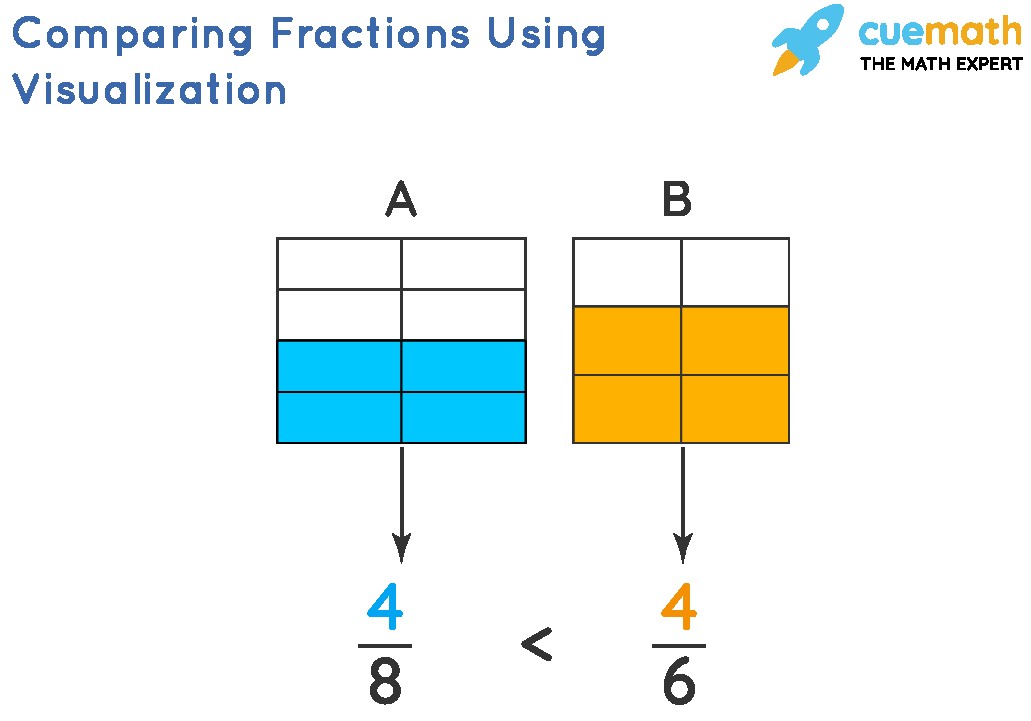
6. Visual Representations: Making Fractions Tangible
Visual aids can be incredibly helpful in understanding and comparing fractions, especially for learners who benefit from visual learning styles.
6.1. Using Fraction Bars or Circles
Fraction bars or circles visually represent fractions as parts of a whole. By comparing the shaded areas, you can quickly determine which fraction is larger.
Example:
Represent 1/2 and 3/4 using fraction circles. It’s easy to see that 3/4 covers more area than 1/2.
6.2. Drawing Diagrams
Drawing your own diagrams can also be effective. For example, you can draw two rectangles of the same size and divide them into the number of parts indicated by the denominators. Then, shade the number of parts indicated by the numerators.
7. Common Mistakes and How to Avoid Them
Comparing fractions can be tricky, and it’s easy to make mistakes. Here are some common errors and how to avoid them:
- Mistake: Assuming that the fraction with the larger numerator is always larger (without considering the denominator).
- Solution: Always consider the denominator. If the denominators are different, find a common denominator before comparing.
- Mistake: Incorrectly finding the Least Common Multiple (LCM).
- Solution: Double-check your multiples and ensure you’ve identified the smallest common multiple.
- Mistake: Making errors in arithmetic when converting fractions to equivalent fractions or decimals.
- Solution: Use a calculator or take your time to ensure accuracy.
8. Real-World Applications and Examples
To truly master comparing fractions, it’s important to see how it’s used in real-world scenarios. Here are some additional examples:
- Baking: A recipe calls for 2/3 cup of flour, but you only want to make half the recipe. You need to determine what half of 2/3 is.
- Sports: A basketball player makes 7/10 of their free throws, while another player makes 3/4. Who has a better free throw percentage?
- Shopping: A store offers 1/4 off a product, while another store offers 20% off the same product. Which discount is better?
- Travel: You’ve driven 2/5 of a journey, and your friend has driven 1/3 of the same journey. Who has driven further?
9. Advanced Fraction Comparisons: Beyond the Basics
Once you’ve mastered the basic comparison methods, you can explore more advanced scenarios, such as comparing multiple fractions or dealing with negative fractions.
9.1. Comparing More Than Two Fractions
To compare more than two fractions, find the LCD of all the denominators and convert all the fractions to equivalent fractions with the LCD. Then, compare the numerators.
Example:
Compare 1/2, 2/5, and 3/10.
- The LCD of 2, 5, and 10 is 10.
- Convert the fractions: 1/2 = 5/10, 2/5 = 4/10, 3/10 = 3/10.
- Now compare the numerators: 5 > 4 > 3.
- Therefore, 1/2 > 2/5 > 3/10.
9.2. Comparing Negative Fractions
When comparing negative fractions, remember that the number closer to zero is larger.
Example:
Compare -1/4 and -1/2.
Think of a number line. -1/4 is closer to zero than -1/2. Therefore, -1/4 > -1/2.
10. Practice Problems to Sharpen Your Skills
To solidify your understanding, work through these practice problems:
- Compare 5/7 and 3/7.
- Compare 2/3 and 3/5.
- Compare 1 1/4 and 1 2/5.
- Compare -2/5 and -1/3.
- Order the following fractions from least to greatest: 1/2, 3/8, 2/5.
(Answers: 1. 5/7 > 3/7, 2. 3/5 > 2/3, 3. 1 2/5 > 1 1/4, 4. -1/3 > -2/5, 5. 3/8, 2/5, 1/2)
Mastering these comparisons not only helps in academics but also in daily activities, emphasizing why COMPARE.EDU.VN is dedicated to offering a complete guide on how we compare fractions.
Comparing fractions is a fundamental mathematical skill that applies to various aspects of life. Whether you are comparing recipes, calculating proportions, or making financial decisions, the ability to confidently compare fractions is essential. By mastering the methods and concepts outlined in this guide, you’ll be well-equipped to tackle any fraction comparison challenge.
FAQ: Everything You Need to Know About Comparing Fractions
1. What is the easiest method for comparing fractions?
The easiest method depends on the fractions themselves. If they have the same denominator, simply compare the numerators. If not, converting them to decimals is often the quickest approach, especially with a calculator.
2. How do you compare fractions with different numerators and denominators?
Find the Least Common Denominator (LCD) or use the cross-multiplication method. Both will give you a clear comparison.
3. What is an equivalent fraction, and how does it help in comparing?
Equivalent fractions have different numerators and denominators but represent the same value (e.g., 1/2 and 2/4). Converting fractions to equivalent forms with a common denominator makes comparison straightforward.
4. How do you compare mixed numbers?
First, compare the whole number parts. If they’re the same, compare the fractional parts using common denominators or cross-multiplication. Alternatively, convert mixed numbers to improper fractions and then compare.
5. Why do we need to compare fractions in real life?
Comparing fractions is crucial in cooking, measuring, finance, time management, and many other daily tasks. It helps you make informed decisions and accurately assess proportions.
6. What is cross-multiplication, and how does it work?
Cross-multiplication involves multiplying the numerator of one fraction by the denominator of the other and vice versa. By comparing the results, you can determine which fraction is larger without finding a common denominator.
7. How can visual aids help in understanding fraction comparisons?
Visual aids like fraction bars or circles provide a tangible representation of fractions, making it easier to see which fraction represents a larger portion of a whole.
8. What are some common mistakes to avoid when comparing fractions?
Common mistakes include ignoring the denominator, incorrectly finding the LCD, and making arithmetic errors during conversions. Always double-check your work and ensure you understand the underlying concepts.
9. How do you compare negative fractions?
Remember that the negative fraction closer to zero is larger. For example, -1/4 is greater than -1/2.
10. How does COMPARE.EDU.VN make comparing fractions easier?
COMPARE.EDU.VN offers comprehensive guides, practical examples, and clear explanations to simplify fraction comparisons. By understanding these methods, you enhance both academic skills and everyday decision-making.
Ready to make comparing fractions a breeze? Visit compare.edu.vn at 333 Comparison Plaza, Choice City, CA 90210, United States, or contact us via WhatsApp at +1 (626) 555-9090 for more resources and expert guidance.