Comparing fractions with different denominators can seem challenging, but it’s a fundamental skill in mathematics and everyday life. This guide, brought to you by COMPARE.EDU.VN, breaks down the process into easy-to-understand steps and methods. Discover how to effectively compare fractions, even when their denominators don’t match, using techniques like finding common denominators, decimal conversion, and visual aids, enhancing your understanding of fractional comparison and numerical relationships.
Table of Contents
- Understanding the Basics of Fractions
- Why is Comparing Fractions Important?
- Methods for Comparing Fractions with Different Denominators
- Step-by-Step Examples of Comparing Fractions with Different Denominators
- Tips and Tricks for Easier Fraction Comparison
- Common Mistakes to Avoid When Comparing Fractions
- Comparing More Than Two Fractions
- Real-World Applications of Comparing Fractions
- Advanced Techniques for Fraction Comparison
- The Role of Technology in Comparing Fractions
- How COMPARE.EDU.VN Simplifies Fraction Comparisons
- Expert Insights on Fraction Comparison
- Comparing Fractions in Different Number Systems
- Fractions and Proportions: A Comparative Analysis
- The Future of Fraction Comparison Techniques
- Challenging Fraction Comparison Problems and Solutions
- Comparing Fractions in Algebraic Equations
- Comparing Fractions and Percentages: A Practical Guide
- The Psychological Aspect of Fraction Comparison
- FAQs About Comparing Fractions with Different Denominators
1. Understanding the Basics of Fractions
Before diving into the methods for comparing fractions with different denominators, it’s crucial to understand what a fraction represents. A fraction is a part of a whole, expressed as a ratio between two numbers: the numerator and the denominator. The numerator represents the number of parts we have, and the denominator represents the total number of equal parts that make up the whole. For example, in the fraction 3/4, 3 is the numerator, and 4 is the denominator, indicating that we have 3 parts out of a total of 4. Recognizing this fundamental concept is key to successfully navigate the comparison process, ensuring you grasp the relationship between the parts and the whole. This understanding lays the groundwork for more advanced techniques like finding common denominators or converting fractions into decimals, making the comparison process much more intuitive and straightforward.
Fractions can be categorized into several types:
- Proper Fractions: The numerator is less than the denominator (e.g., 2/5).
- Improper Fractions: The numerator is greater than or equal to the denominator (e.g., 7/3).
- Mixed Numbers: A whole number combined with a proper fraction (e.g., 1 1/2).
2. Why is Comparing Fractions Important?
Comparing fractions is not just an academic exercise; it has practical applications in various aspects of life. Whether you’re baking a cake, managing your finances, or analyzing data, the ability to compare fractions accurately is essential. In cooking, you might need to adjust ingredient quantities based on a recipe that uses fractional measurements. In finance, comparing fractions can help you determine which investment offers a better return. Moreover, understanding how fractions relate to each other enhances your problem-solving skills and logical reasoning, which are valuable in both personal and professional settings. Proficiency in comparing fractions ensures that you can make informed decisions and solve real-world problems with confidence, highlighting its significance beyond the classroom.
Here are some areas where comparing fractions is useful:
- Cooking: Adjusting recipes and ingredient proportions.
- Finance: Comparing investment returns or loan interest rates.
- Construction: Measuring materials and calculating dimensions.
- Data Analysis: Interpreting and comparing statistical data.
- Everyday Life: Making informed decisions about purchases, time management, and resource allocation.
3. Methods for Comparing Fractions with Different Denominators
When comparing fractions, especially those with different denominators, several methods can be employed to simplify the process. These methods include finding a common denominator, cross-multiplication, converting fractions to decimals, and using visual models. Each technique offers a unique approach to making fractions comparable, catering to different learning styles and problem-solving preferences. Whether you prefer the algebraic precision of finding a common denominator or the intuitive nature of visual aids, mastering these methods equips you with the tools to confidently compare fractions in any situation. Understanding and practicing these techniques ensures that you can accurately determine the relative size of fractions, regardless of their initial form.
3.1 Finding a Common Denominator (LCD Method)
The most common method for comparing fractions with different denominators involves finding a common denominator. This is typically the least common denominator (LCD), which is the smallest multiple that both denominators share. Once the fractions have the same denominator, you can easily compare the numerators. The fraction with the larger numerator is the larger fraction. This method ensures that you are comparing fractions with equivalent parts, making the comparison straightforward and accurate. By converting fractions to have the same denominator, you create a level playing field, allowing you to focus solely on the numerators to determine which fraction represents a larger portion of the whole.
Here’s how to find the LCD:
- List the multiples of each denominator.
- Identify the smallest multiple that appears in both lists.
- Convert each fraction to an equivalent fraction with the LCD as the denominator.
- Compare the numerators.
Example:
Compare 1/3 and 2/5.
- Multiples of 3: 3, 6, 9, 12, 15
- Multiples of 5: 5, 10, 15
- LCD = 15
Convert the fractions:
- 1/3 = (1 5) / (3 5) = 5/15
- 2/5 = (2 3) / (5 3) = 6/15
Since 6/15 is greater than 5/15, 2/5 is greater than 1/3.
3.2 Cross-Multiplication Method
Cross-multiplication is a quick and efficient method for comparing two fractions. This technique involves multiplying the numerator of the first fraction by the denominator of the second fraction, and vice versa. The resulting products are then compared to determine which fraction is larger. Specifically, if the product of the first fraction’s numerator and the second fraction’s denominator is greater than the product of the second fraction’s numerator and the first fraction’s denominator, then the first fraction is larger. This method bypasses the need to find a common denominator, making it a useful shortcut, especially in time-sensitive situations. Cross-multiplication provides a straightforward, algebraic approach to comparing fractions, ideal for quick comparisons and problem-solving.
Here’s how to use cross-multiplication:
- Multiply the numerator of the first fraction by the denominator of the second fraction.
- Multiply the numerator of the second fraction by the denominator of the first fraction.
- Compare the two products.
Example:
Compare 3/4 and 5/7.
- 3 * 7 = 21
- 5 * 4 = 20
Since 21 is greater than 20, 3/4 is greater than 5/7.
3.3 Converting to Decimals
Converting fractions to decimals is a straightforward method that allows for easy comparison using decimal values. To convert a fraction to a decimal, simply divide the numerator by the denominator. Once both fractions are in decimal form, comparing them becomes as easy as comparing decimal numbers. This method is particularly useful when dealing with fractions that are difficult to convert to a common denominator or when you prefer working with decimals. Converting to decimals provides a clear and direct way to assess the relative size of fractions, making it a valuable tool in various mathematical and real-world contexts.
Here’s how to convert to decimals:
- Divide the numerator by the denominator for each fraction.
- Compare the resulting decimal values.
Example:
Compare 2/5 and 3/8.
- 2/5 = 0.4
- 3/8 = 0.375
Since 0.4 is greater than 0.375, 2/5 is greater than 3/8.
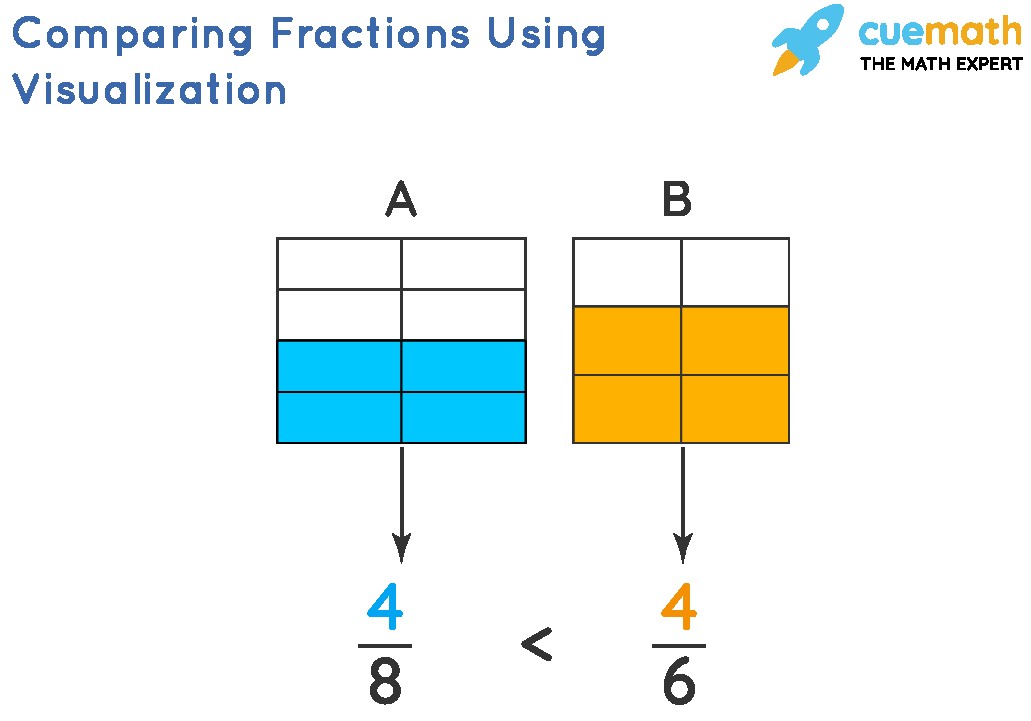
3.4 Using Visual Models
Visual models, such as fraction bars or pie charts, provide an intuitive way to compare fractions, especially for visual learners. Fraction bars are rectangular bars divided into equal parts, with each part representing a fraction of the whole. Pie charts, on the other hand, divide a circle into sectors, with each sector representing a fraction of the whole. By visually representing fractions using these models, you can directly compare the sizes of the fractional parts. This method is particularly helpful for understanding the concept of fractions and making comparisons more concrete. Visual models offer a hands-on approach to fraction comparison, fostering a deeper understanding and making the process more accessible.
Here’s how to use visual models:
- Draw or use pre-made fraction bars or pie charts.
- Divide each model into the number of parts indicated by the denominator.
- Shade the number of parts indicated by the numerator.
- Compare the shaded areas to determine which fraction is larger.
Example:
To compare 1/4 and 1/3, draw two fraction bars. Divide one into four equal parts and shade one part (1/4). Divide the other into three equal parts and shade one part (1/3). Visually, it’s clear that 1/3 is larger than 1/4.
4. Step-by-Step Examples of Comparing Fractions with Different Denominators
To solidify your understanding of comparing fractions with different denominators, let’s walk through several step-by-step examples using the methods we’ve discussed. These examples will illustrate how to apply each technique effectively, providing you with a practical guide to fraction comparison. By working through these examples, you’ll gain confidence in your ability to compare fractions accurately and efficiently, regardless of the specific numbers involved. This hands-on approach ensures that you not only understand the theory but can also apply it in practice.
Example 1: Using the LCD Method
Compare 2/3 and 3/5.
- Find the LCD of 3 and 5: The LCD is 15.
- Convert 2/3 to an equivalent fraction with a denominator of 15: (2 5) / (3 5) = 10/15.
- Convert 3/5 to an equivalent fraction with a denominator of 15: (3 3) / (5 3) = 9/15.
- Compare the numerators: 10 > 9.
Therefore, 2/3 is greater than 3/5.
Example 2: Using Cross-Multiplication
Compare 4/7 and 5/9.
- Multiply 4 * 9 = 36.
- Multiply 5 * 7 = 35.
- Compare the products: 36 > 35.
Therefore, 4/7 is greater than 5/9.
Example 3: Converting to Decimals
Compare 1/8 and 2/9.
- Convert 1/8 to a decimal: 1 ÷ 8 = 0.125.
- Convert 2/9 to a decimal: 2 ÷ 9 = 0.222…
- Compare the decimal values: 0.222… > 0.125.
Therefore, 2/9 is greater than 1/8.
Example 4: Using Visual Models
Compare 2/5 and 3/10.
- Draw two fraction bars.
- Divide the first bar into five equal parts and shade two parts (2/5).
- Divide the second bar into ten equal parts and shade three parts (3/10).
- Visually, 2/5 appears larger than 3/10. To confirm, notice that 2/5 is equivalent to 4/10, which is greater than 3/10.
Therefore, 2/5 is greater than 3/10.
5. Tips and Tricks for Easier Fraction Comparison
Comparing fractions can be made simpler with a few helpful tips and tricks. These techniques can save you time and reduce the likelihood of errors. For instance, understanding how to quickly find a common denominator or recognizing when cross-multiplication is the most efficient method can streamline the comparison process. Additionally, developing a strong number sense and familiarity with common fractions can help you make quick estimations and mental comparisons. By incorporating these strategies into your problem-solving approach, you can enhance your fraction comparison skills and tackle more complex problems with ease.
Here are some useful tips:
- Simplify Fractions First: If possible, simplify each fraction before comparing them.
- Use Benchmarks: Compare fractions to benchmarks like 1/2 or 1. For example, if one fraction is less than 1/2 and the other is greater, the latter is larger.
- Estimate: Develop a sense of fraction sizes. For instance, recognize that 3/7 is slightly less than 1/2.
- Recognize Equivalent Fractions: Knowing common equivalent fractions can help you quickly compare fractions.
- Practice Regularly: The more you practice, the easier it will become to compare fractions quickly and accurately.
6. Common Mistakes to Avoid When Comparing Fractions
When comparing fractions, it’s essential to be aware of common mistakes that can lead to incorrect conclusions. One frequent error is assuming that the fraction with the larger denominator is always smaller, without considering the numerator. Another mistake is failing to find a common denominator before comparing fractions, which can result in an inaccurate assessment of their relative sizes. Additionally, not simplifying fractions before comparing them can make the process more complex and increase the chances of error. By avoiding these pitfalls, you can ensure that your fraction comparisons are accurate and reliable.
Here are some common mistakes to watch out for:
- Ignoring the Numerator: Assuming that a larger denominator always means a smaller fraction.
- Not Finding a Common Denominator: Trying to compare fractions without a common denominator can lead to errors.
- Incorrectly Applying Cross-Multiplication: Make sure to multiply the correct numerators and denominators.
- Not Simplifying Fractions: Failing to simplify fractions can make the comparison more difficult.
- Misinterpreting Visual Models: Ensure that your visual models accurately represent the fractions.
7. Comparing More Than Two Fractions
Comparing more than two fractions requires a systematic approach to ensure accuracy. One effective method is to find a common denominator for all the fractions, allowing you to directly compare their numerators. Alternatively, you can convert each fraction to a decimal and then compare the decimal values. Another strategy is to compare pairs of fractions, gradually narrowing down the order from largest to smallest. Regardless of the method you choose, organization and attention to detail are crucial when dealing with multiple fractions. By employing a methodical approach, you can confidently compare and order multiple fractions with ease.
Here’s how to compare more than two fractions:
- Find the least common denominator (LCD) for all fractions.
- Convert each fraction to an equivalent fraction with the LCD as the denominator.
- Compare the numerators to determine the order of the fractions.
Example:
Compare 1/2, 2/3, and 3/4.
- The LCD of 2, 3, and 4 is 12.
- Convert the fractions:
- 1/2 = 6/12
- 2/3 = 8/12
- 3/4 = 9/12
- Compare the numerators: 6 < 8 < 9.
Therefore, the order from smallest to largest is 1/2, 2/3, and 3/4.
8. Real-World Applications of Comparing Fractions
Comparing fractions is not just a theoretical exercise; it has numerous practical applications in everyday life. From cooking and baking to managing finances and making informed decisions, the ability to compare fractions accurately is essential. In the kitchen, you might need to adjust ingredient quantities based on fractional measurements. In personal finance, you can compare interest rates or investment returns to make sound financial decisions. Furthermore, understanding fractions is crucial in fields like construction, engineering, and data analysis. By recognizing the real-world relevance of fraction comparison, you can appreciate its importance and strive to master this fundamental skill.
Here are some real-world applications:
- Cooking and Baking: Adjusting recipes and ingredient proportions.
- Finance: Comparing interest rates, investment returns, and discounts.
- Construction: Measuring materials and calculating dimensions.
- Shopping: Comparing prices per unit to find the best deals.
- Time Management: Allocating time to different tasks based on fractional parts of the day.
9. Advanced Techniques for Fraction Comparison
For those looking to deepen their understanding of fraction comparison, several advanced techniques can be explored. These methods go beyond the basics and offer more sophisticated approaches to solving complex problems. One such technique involves using number theory to simplify fractions or find common denominators more efficiently. Another advanced method involves comparing fractions using inequalities and algebraic manipulations. By mastering these advanced techniques, you can tackle more challenging fraction comparison problems with confidence and precision.
Here are some advanced techniques:
- Using Number Theory: Employing prime factorization and other number theory concepts to simplify fractions and find common denominators.
- Algebraic Inequalities: Applying algebraic principles to compare fractions using inequalities.
- Modular Arithmetic: Using modular arithmetic to simplify fraction comparison in specific contexts.
10. The Role of Technology in Comparing Fractions
Technology plays a significant role in simplifying and enhancing the process of comparing fractions. Numerous online tools and calculators are available to assist with fraction comparison, making it quicker and more accurate. These tools can perform complex calculations, convert fractions to decimals, and provide visual representations of fractions, catering to different learning styles. Moreover, educational apps and software offer interactive lessons and practice exercises to improve your understanding of fractions. By leveraging technology, you can overcome the challenges of manual fraction comparison and focus on developing a deeper conceptual understanding.
Here are some technological tools for comparing fractions:
- Online Fraction Calculators: Websites that allow you to enter fractions and compare them instantly.
- Educational Apps: Interactive apps that teach fraction comparison through games and exercises.
- Spreadsheet Software: Programs like Excel that can convert fractions to decimals and compare them easily.
11. How COMPARE.EDU.VN Simplifies Fraction Comparisons
COMPARE.EDU.VN offers a comprehensive platform designed to simplify fraction comparisons and enhance your understanding of this fundamental mathematical concept. Our website provides a range of tools and resources, including interactive calculators, step-by-step tutorials, and visual aids, to make fraction comparison more accessible and intuitive. Whether you’re a student, a professional, or simply someone looking to improve your math skills, COMPARE.EDU.VN offers the resources you need to master fraction comparison.
Here’s how COMPARE.EDU.VN can help:
- Interactive Calculators: Quickly compare fractions using our user-friendly calculators.
- Step-by-Step Tutorials: Learn different methods for comparing fractions with detailed explanations.
- Visual Aids: Use visual models to understand and compare fractions more intuitively.
- Practice Exercises: Test your knowledge with a variety of practice exercises and quizzes.
- Expert Insights: Access expert tips and strategies for mastering fraction comparison.
12. Expert Insights on Fraction Comparison
To provide you with a deeper understanding of fraction comparison, we’ve gathered insights from math experts and educators. These experts emphasize the importance of developing a strong conceptual understanding of fractions rather than relying solely on rote memorization. They recommend using visual models and real-world examples to make fractions more concrete and relatable. Additionally, they highlight the value of practice and repetition in mastering fraction comparison skills. By incorporating these expert insights into your learning approach, you can build a solid foundation in fraction comparison and excel in mathematics.
Here are some expert insights:
- Focus on Conceptual Understanding: Understand the meaning of fractions and their relationships to each other.
- Use Visual Models: Employ visual aids to make fractions more concrete and understandable.
- Practice Regularly: Consistent practice is key to mastering fraction comparison skills.
- Relate to Real-World Examples: Connect fractions to real-life situations to make them more relatable.
13. Comparing Fractions in Different Number Systems
While most fraction comparisons are done in the decimal number system, understanding how to compare fractions in other number systems can be a valuable skill. Different number systems, such as binary, octal, and hexadecimal, use different bases to represent numbers. Converting fractions to these number systems and comparing them can provide insights into their relative values in different contexts. This advanced topic is particularly relevant in computer science and engineering, where different number systems are commonly used.
Here are some key points:
- Binary Fractions: Fractions in base-2 (binary) can be compared by converting them to a common denominator or decimal equivalent.
- Octal and Hexadecimal Fractions: Similar methods apply to fractions in base-8 (octal) and base-16 (hexadecimal).
- Conversion: Converting fractions to different number systems often involves repeated division or multiplication by the base.
14. Fractions and Proportions: A Comparative Analysis
Fractions and proportions are closely related concepts in mathematics, and understanding their relationship can enhance your ability to solve problems involving ratios and comparisons. A proportion is an equation that states that two ratios (fractions) are equal. Comparing fractions is often a necessary step in solving proportions, as you need to determine whether two fractions are equivalent. By understanding the interplay between fractions and proportions, you can tackle a wider range of mathematical problems with greater confidence.
Key aspects of their relationship include:
- Equivalence: Proportions are based on the equivalence of two fractions.
- Solving Proportions: Comparing fractions helps determine if a proportion is true or false.
- Applications: Proportions are used in various real-world scenarios, such as scaling recipes and calculating percentages.
15. The Future of Fraction Comparison Techniques
As technology continues to advance, the techniques for comparing fractions are likely to evolve as well. Artificial intelligence (AI) and machine learning (ML) could play a role in developing more efficient and intuitive methods for fraction comparison. For example, AI-powered educational tools could provide personalized learning experiences, tailoring the difficulty of fraction comparison problems to each student’s skill level. Additionally, virtual and augmented reality (VR/AR) could offer immersive visual models for understanding fractions, making the learning process more engaging and effective.
Potential future developments include:
- AI-Powered Tools: Personalized learning experiences for fraction comparison.
- VR/AR Visualizations: Immersive visual models for understanding fractions.
- Automated Simplification: Algorithms that automatically simplify fractions for easier comparison.
16. Challenging Fraction Comparison Problems and Solutions
To test your fraction comparison skills, let’s tackle some challenging problems and explore their solutions. These problems will require you to apply the techniques and strategies we’ve discussed in this guide, pushing you to think critically and creatively. By working through these examples, you’ll gain confidence in your ability to solve complex fraction comparison problems.
Problem 1:
Which is larger: 5/8 or 7/11?
Solution:
Using cross-multiplication:
- 5 * 11 = 55
- 7 * 8 = 56
Since 56 > 55, 7/11 is larger.
Problem 2:
Order the following fractions from smallest to largest: 2/5, 3/7, and 4/9.
Solution:
Find a common denominator:
- The LCD of 5, 7, and 9 is 315.
- Convert the fractions:
- 2/5 = 126/315
- 3/7 = 135/315
- 4/9 = 140/315
Therefore, the order from smallest to largest is 2/5, 3/7, and 4/9.
17. Comparing Fractions in Algebraic Equations
Fractions often appear in algebraic equations, and understanding how to compare them in this context is crucial for solving these equations. When dealing with equations involving fractions, you may need to compare fractions to determine whether two expressions are equal or to solve for an unknown variable. Techniques such as finding a common denominator and cross-multiplication can be applied to compare fractions in algebraic equations, allowing you to simplify the equations and find solutions.
Key strategies include:
- Finding a Common Denominator: Combining fractions in equations often requires a common denominator.
- Cross-Multiplication: Useful for solving equations where two fractions are equal.
- Simplification: Simplifying fractions can make equations easier to solve.
18. Comparing Fractions and Percentages: A Practical Guide
Fractions and percentages are both used to represent parts of a whole, and understanding how to convert between them is essential for making comparisons. To convert a fraction to a percentage, simply multiply the fraction by 100. Once you have both values in percentage form, comparing them becomes straightforward. This conversion is particularly useful in real-world scenarios, such as calculating discounts, understanding statistics, and interpreting data.
Here’s how to compare fractions and percentages:
- Convert the fraction to a percentage by multiplying by 100.
- Compare the resulting percentage to the given percentage.
Example:
Compare 3/4 to 70%.
- Convert 3/4 to a percentage: (3/4) * 100 = 75%.
- Compare 75% to 70%.
Since 75% > 70%, 3/4 is greater than 70%.
19. The Psychological Aspect of Fraction Comparison
Research in cognitive psychology has revealed that people often struggle with fraction comparison due to various cognitive biases and heuristics. One common bias is the “whole number bias,” where people tend to focus on the whole number components of fractions (i.e., the numerator and denominator) rather than their proportional relationship. This can lead to errors in judgment, especially when comparing fractions with large numerators and denominators. Understanding these psychological factors can help you develop strategies to overcome these biases and make more accurate fraction comparisons.
Key findings include:
- Whole Number Bias: Focusing on the whole number components of fractions rather than their proportional relationship.
- Magnitude Effect: The difficulty of comparing fractions increases as the numbers get larger.
- Cognitive Load: Fraction comparison can be cognitively demanding, leading to errors when mental resources are limited.
20. FAQs About Comparing Fractions with Different Denominators
Here are some frequently asked questions about comparing fractions with different denominators:
Q1: What is the easiest method for comparing fractions with different denominators?
The easiest method depends on the specific fractions, but converting to decimals is often straightforward.
Q2: Why is it important to find a common denominator?
Finding a common denominator allows you to compare fractions with equivalent parts, making the comparison accurate.
Q3: Can I use cross-multiplication for comparing more than two fractions?
No, cross-multiplication is only suitable for comparing two fractions at a time.
Q4: What if the fractions are negative?
When comparing negative fractions, remember that the fraction closer to zero is larger.
Q5: How do I compare mixed numbers with different denominators?
First, convert the mixed numbers to improper fractions, then use any of the methods discussed to compare the fractions.
Q6: Is there a shortcut for comparing fractions with the same numerator?
Yes, if the numerators are the same, the fraction with the smaller denominator is larger.
Q7: What should I do if the denominators are very large?
If the denominators are very large, converting to decimals is often the most practical approach.
Q8: Can I use a calculator to compare fractions?
Yes, calculators can be helpful, especially for complex fractions, but it’s important to understand the underlying concepts.
Q9: How does comparing fractions relate to real-world situations?
Comparing fractions is used in various real-world scenarios, such as cooking, finance, and construction.
Q10: What if the fractions are part of a larger problem?
If the fractions are part of a larger problem, focus on simplifying and solving the overall problem rather than just comparing the fractions in isolation.
Ready to put your fraction comparison skills to the test? Visit compare.edu.vn for interactive tools, tutorials, and practice exercises to help you master fractions and make informed decisions. Contact us at 333 Comparison Plaza, Choice City, CA 90210, United States or Whatsapp: +1 (626) 555-9090. Start comparing fractions with confidence today.