How Do You Compare 2 Fractions? The Ultimate Guide

Comparing two fractions involves determining which fraction has a greater value. This comprehensive guide on How To Compare 2 Fractions provides various methods, from basic comparisons with common denominators to more complex techniques involving unlike denominators, decimal conversions, and visual aids. Discover the easiest and most efficient strategies at COMPARE.EDU.VN to master comparing fractions and enhance your number sense, along with understanding relative sizes.

1. Understanding the Basics of Comparing Fractions

Before delving into the methods of comparing fractions, it’s crucial to understand what a fraction represents. A fraction is a part of a whole, consisting of two main components: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts of the whole are being considered, while the denominator represents the total number of equal parts that make up the whole.

1.1 What is a Fraction?

A fraction represents a part of a whole. It’s written as one number over another, separated by a line. The number above the line is the numerator, and the number below the line is the denominator. For example, in the fraction 3/4, 3 is the numerator, and 4 is the denominator. This means we are considering 3 parts out of a total of 4 equal parts. Fractions are fundamental in various real-life scenarios, from cooking and measuring to understanding proportions and ratios.

1.2 Why is Comparing Fractions Important?

Understanding how to compare 2 fractions is essential because it helps us determine which fraction represents a larger or smaller portion of a whole. This skill is crucial in many practical situations, such as:

• Cooking: Adjusting recipes based on the number of servings.
• Finance: Comparing investment returns or discounts.
• Construction: Measuring materials and planning layouts.
• Education: Understanding proportions and ratios in mathematics.

Without the ability to compare fractions, making informed decisions in these areas becomes significantly more challenging. Mastering this skill enhances your overall number sense and mathematical proficiency.

2. Methods for Comparing Fractions

Several methods exist for comparing fractions, each suited to different scenarios. These include comparing fractions with the same denominators, fractions with different denominators, using decimal equivalents, visualization techniques, and cross-multiplication. Here’s a detailed look at each approach:

2.1 Comparing Fractions with the Same Denominators

The simplest method for comparing fractions is when they have the same denominator. In this case, you only need to compare the numerators. The fraction with the larger numerator is the larger fraction.

2.1.1 How to Compare Fractions with the Same Denominator

1. Identify the Denominators: Ensure that both fractions have the same denominator.
2. Compare the Numerators: Look at the numerators of both fractions.
3. Determine the Larger Fraction: The fraction with the larger numerator is the larger fraction.

For example, comparing 3/8 and 5/8:

• Both fractions have the same denominator (8).
• Compare the numerators: 3 and 5.
• Since 5 is greater than 3, 5/8 is larger than 3/8.

2.1.2 Examples of Comparing Fractions with the Same Denominator

Let’s consider a few more examples to illustrate this method:

• Example 1: Compare 7/12 and 9/12.
  • Both fractions have the same denominator (12).
  • Compare the numerators: 7 and 9.
  • Since 9 is greater than 7, 9/12 is larger than 7/12.
• Example 2: Compare 11/15 and 8/15.
  • Both fractions have the same denominator (15).
  • Compare the numerators: 11 and 8.
  • Since 11 is greater than 8, 11/15 is larger than 8/15.
• Example 3: Compare 4/5 and 2/5.
  • Both fractions have the same denominator (5).
  • Compare the numerators: 4 and 2.
  • Since 4 is greater than 2, 4/5 is larger than 2/5.

2.2 Comparing Fractions with Unlike Denominators

When fractions have different denominators, you need to find a common denominator before comparing them. The most common method is to find the least common multiple (LCM) of the denominators.

2.2.1 Finding the Least Common Multiple (LCM)

The least common multiple (LCM) is the smallest number that is a multiple of both denominators. To find the LCM:

1. List the Multiples: List the multiples of each denominator.
2. Identify the Common Multiples: Find the smallest multiple that both denominators share.

For example, to find the LCM of 4 and 6:

• Multiples of 4: 4, 8, 12, 16, 20, 24, …
• Multiples of 6: 6, 12, 18, 24, 30, …
• The LCM of 4 and 6 is 12.

2.2.2 Converting Fractions to a Common Denominator

Once you find the LCM, convert each fraction so that its denominator is the LCM. To do this, multiply both the numerator and the denominator of each fraction by the number that makes the denominator equal to the LCM.

For example, to convert 1/4 and 2/6 to fractions with a denominator of 12:

• For 1/4, multiply both the numerator and the denominator by 3: (1 3) / (4 3) = 3/12.
• For 2/6, multiply both the numerator and the denominator by 2: (2 2) / (6 2) = 4/12.

2.2.3 Comparing Fractions with a Common Denominator

After converting the fractions to a common denominator, you can compare the numerators as you would with fractions that originally had the same denominator.

Using the previous example:

• We converted 1/4 to 3/12 and 2/6 to 4/12.
• Now, compare the numerators: 3 and 4.
• Since 4 is greater than 3, 4/12 (or 2/6) is larger than 3/12 (or 1/4).

2.2.4 Examples of Comparing Fractions with Unlike Denominators

Let’s look at additional examples to reinforce this method:

• Example 1: Compare 2/3 and 3/5.
  • Find the LCM of 3 and 5: The LCM is 15.
  • Convert 2/3 to a fraction with a denominator of 15: (2 5) / (3 5) = 10/15.
  • Convert 3/5 to a fraction with a denominator of 15: (3 3) / (5 3) = 9/15.
  • Compare the numerators: 10 and 9.
  • Since 10 is greater than 9, 2/3 is larger than 3/5.
• Example 2: Compare 1/2 and 3/7.
  • Find the LCM of 2 and 7: The LCM is 14.
  • Convert 1/2 to a fraction with a denominator of 14: (1 7) / (2 7) = 7/14.
  • Convert 3/7 to a fraction with a denominator of 14: (3 2) / (7 2) = 6/14.
  • Compare the numerators: 7 and 6.
  • Since 7 is greater than 6, 1/2 is larger than 3/7.
• Example 3: Compare 4/9 and 5/12.
  • Find the LCM of 9 and 12: The LCM is 36.
  • Convert 4/9 to a fraction with a denominator of 36: (4 4) / (9 4) = 16/36.
  • Convert 5/12 to a fraction with a denominator of 36: (5 3) / (12 3) = 15/36.
  • Compare the numerators: 16 and 15.
  • Since 16 is greater than 15, 4/9 is larger than 5/12.

2.3 Decimal Method of Comparing Fractions

Another effective method for comparing fractions is to convert them into decimal numbers. This involves dividing the numerator by the denominator to obtain a decimal value, which can then be easily compared.

2.3.1 Converting Fractions to Decimals

To convert a fraction to a decimal, divide the numerator by the denominator. For example:

• To convert 3/4 to a decimal, divide 3 by 4: 3 ÷ 4 = 0.75.
• To convert 1/2 to a decimal, divide 1 by 2: 1 ÷ 2 = 0.5.

2.3.2 Comparing Decimal Values

Once you have the decimal values, compare them as you would with any other decimal numbers.

For example, comparing 0.75 and 0.5:

• 0. 75 is greater than 0.5, so 3/4 is larger than 1/2.

2.3.3 Examples of the Decimal Method

Let’s consider a few more examples to illustrate this method:

• Example 1: Compare 2/5 and 3/8.
  • Convert 2/5 to a decimal: 2 ÷ 5 = 0.4.
  • Convert 3/8 to a decimal: 3 ÷ 8 = 0.375.
  • Compare the decimal values: 0.4 and 0.375.
  • Since 0.4 is greater than 0.375, 2/5 is larger than 3/8.
• Example 2: Compare 5/6 and 7/9.
  • Convert 5/6 to a decimal: 5 ÷ 6 = 0.8333… (approximately 0.83).
  • Convert 7/9 to a decimal: 7 ÷ 9 = 0.7777… (approximately 0.78).
  • Compare the decimal values: 0.83 and 0.78.
  • Since 0.83 is greater than 0.78, 5/6 is larger than 7/9.
• Example 3: Compare 1/3 and 2/7.
  • Convert 1/3 to a decimal: 1 ÷ 3 = 0.3333… (approximately 0.33).
  • Convert 2/7 to a decimal: 2 ÷ 7 = 0.2857… (approximately 0.29).
  • Compare the decimal values: 0.33 and 0.29.
  • Since 0.33 is greater than 0.29, 1/3 is larger than 2/7.

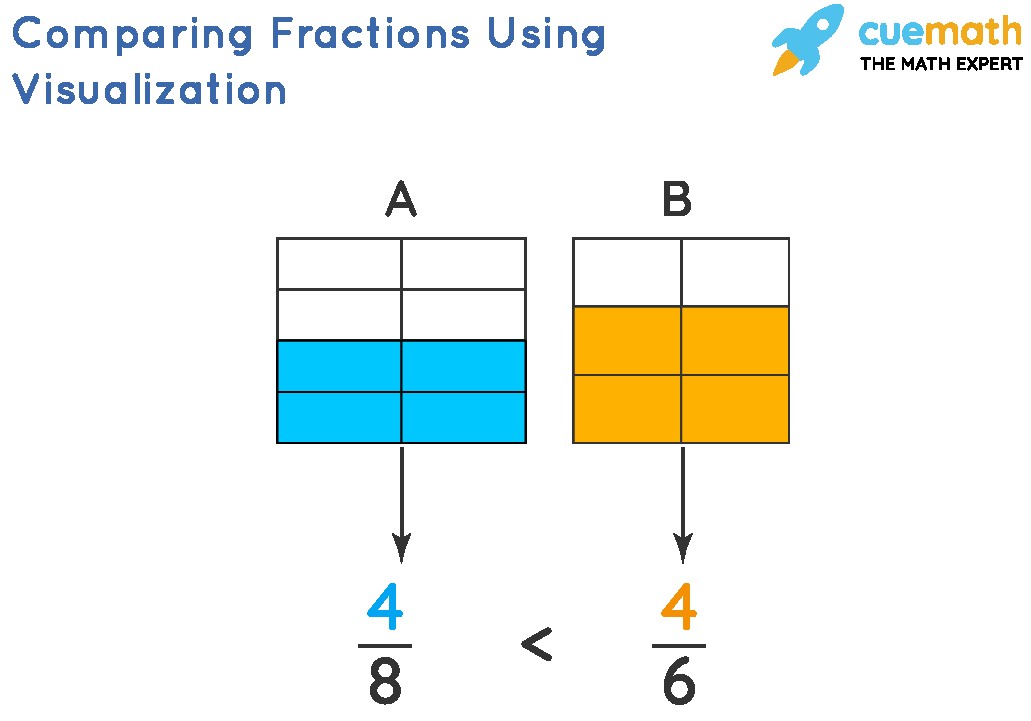
2.4 Comparing Fractions Using Visualization

Visual methods can be particularly helpful for understanding and comparing fractions, especially for those who are visual learners. These methods involve using diagrams or models to represent fractions, making it easier to see their relative sizes.

2.4.1 Using Fraction Bars or Circles

Fraction bars or circles are common visual aids that divide a whole into equal parts. Each part represents a fraction of the whole, and comparing the shaded areas of different fraction bars or circles can help determine which fraction is larger.

For example, to compare 1/2 and 3/4 using fraction bars:

• Draw a fraction bar divided into 2 equal parts and shade 1 part to represent 1/2.
• Draw another fraction bar divided into 4 equal parts and shade 3 parts to represent 3/4.
• Visually, it’s clear that the shaded area representing 3/4 is larger than the shaded area representing 1/2, so 3/4 is larger than 1/2.

2.4.2 Drawing Diagrams

You can also draw your own diagrams to represent fractions. This method is particularly useful when dealing with fractions that are not easily represented by standard fraction bars or circles.

For example, to compare 2/5 and 3/7 using diagrams:

• Draw a rectangle and divide it into 5 equal parts, then shade 2 parts to represent 2/5.
• Draw another rectangle of the same size and divide it into 7 equal parts, then shade 3 parts to represent 3/7.
• By visually comparing the shaded areas, you can determine which fraction represents a larger portion of the whole. In this case, 2/5 appears to be slightly larger than 3/7.

2.4.3 Examples of Visual Comparison

Let’s consider a few more examples to illustrate this method:

• Example 1: Compare 1/4 and 2/8.
  • Draw a fraction bar divided into 4 equal parts and shade 1 part to represent 1/4.
  • Draw another fraction bar divided into 8 equal parts and shade 2 parts to represent 2/8.
  • Visually, the shaded areas are the same, so 1/4 is equal to 2/8.
• Example 2: Compare 2/3 and 5/6.
  • Draw a fraction bar divided into 3 equal parts and shade 2 parts to represent 2/3.
  • Draw another fraction bar divided into 6 equal parts and shade 5 parts to represent 5/6.
  • Visually, the shaded area representing 5/6 is larger than the shaded area representing 2/3, so 5/6 is larger than 2/3.
• Example 3: Compare 3/5 and 4/7.
  • Draw a rectangle divided into 5 equal parts and shade 3 parts to represent 3/5.
  • Draw another rectangle of the same size and divide it into 7 equal parts and shade 4 parts to represent 4/7.
  • By visually comparing the shaded areas, you can determine that 3/5 is larger than 4/7.

2.5 Comparing Fractions Using Cross Multiplication

Cross multiplication is a quick and efficient algebraic method for comparing two fractions. It involves multiplying the numerator of each fraction by the denominator of the other fraction and then comparing the resulting products.

2.5.1 How to Cross Multiply Fractions

1. Set Up the Fractions: Write the two fractions you want to compare side by side.
2. Cross Multiply: Multiply the numerator of the first fraction by the denominator of the second fraction. Write this product next to the first fraction.
3. Multiply the Other Way: Multiply the numerator of the second fraction by the denominator of the first fraction. Write this product next to the second fraction.
4. Compare the Products: Compare the two products. The fraction corresponding to the larger product is the larger fraction.

For example, to compare 1/2 and 3/4 using cross multiplication:

• Set up the fractions: 1/2 and 3/4.
• Cross multiply: 1 * 4 = 4 (write 4 next to 1/2).
• Multiply the other way: 3 * 2 = 6 (write 6 next to 3/4).
• Compare the products: 4 and 6.
• Since 6 is greater than 4, 3/4 is larger than 1/2.

2.5.2 Examples of Cross Multiplication

Let’s consider a few more examples to illustrate this method:

• Example 1: Compare 2/3 and 4/5.
  • Set up the fractions: 2/3 and 4/5.
  • Cross multiply: 2 * 5 = 10 (write 10 next to 2/3).
  • Multiply the other way: 4 * 3 = 12 (write 12 next to 4/5).
  • Compare the products: 10 and 12.
  • Since 12 is greater than 10, 4/5 is larger than 2/3.
• Example 2: Compare 3/7 and 2/5.
  • Set up the fractions: 3/7 and 2/5.
  • Cross multiply: 3 * 5 = 15 (write 15 next to 3/7).
  • Multiply the other way: 2 * 7 = 14 (write 14 next to 2/5).
  • Compare the products: 15 and 14.
  • Since 15 is greater than 14, 3/7 is larger than 2/5.
• Example 3: Compare 5/8 and 7/12.
  • Set up the fractions: 5/8 and 7/12.
  • Cross multiply: 5 * 12 = 60 (write 60 next to 5/8).
  • Multiply the other way: 7 * 8 = 56 (write 56 next to 7/12).
  • Compare the products: 60 and 56.
  • Since 60 is greater than 56, 5/8 is larger than 7/12.

3. Special Cases in Comparing Fractions

Some scenarios require additional considerations. These include comparing negative fractions, mixed numbers, and improper fractions.

3.1 Comparing Negative Fractions

When comparing negative fractions, remember that the fraction with the smaller absolute value is larger. In other words, the fraction closer to zero is greater.

3.1.1 How to Compare Negative Fractions

1. Ignore the Negative Signs: Temporarily disregard the negative signs and compare the fractions as if they were positive.
2. Determine the Larger Fraction (Ignoring Signs): Find the larger fraction using any of the methods described above.
3. Reverse the Comparison: Since the fractions are negative, the fraction that was smaller in the positive comparison is actually larger.

For example, to compare -1/2 and -1/4:

• Ignore the negative signs and compare 1/2 and 1/4.
• 1/2 is larger than 1/4.
• Reverse the comparison: -1/4 is larger than -1/2.

3.1.2 Examples of Negative Fraction Comparisons

Let’s consider additional examples:

• Example 1: Compare -2/3 and -3/5.
  • Ignore the negative signs and compare 2/3 and 3/5.
  • Using cross multiplication: 2 5 = 10 and 3 3 = 9. So, 2/3 is larger than 3/5.
  • Reverse the comparison: -3/5 is larger than -2/3.
• Example 2: Compare -5/6 and -7/8.
  • Ignore the negative signs and compare 5/6 and 7/8.
  • Using cross multiplication: 5 8 = 40 and 7 6 = 42. So, 7/8 is larger than 5/6.
  • Reverse the comparison: -5/6 is larger than -7/8.
• Example 3: Compare -1/5 and -1/3.
  • Ignore the negative signs and compare 1/5 and 1/3.
  • Using cross multiplication: 1 3 = 3 and 1 5 = 5. So, 1/3 is larger than 1/5.
  • Reverse the comparison: -1/5 is larger than -1/3.

3.2 Comparing Mixed Numbers

A mixed number is a combination of a whole number and a fraction (e.g., 2 1/2). To compare mixed numbers, first compare the whole number parts. If the whole numbers are different, the mixed number with the larger whole number is larger. If the whole numbers are the same, compare the fractional parts.

3.2.1 How to Compare Mixed Numbers

1. Compare Whole Numbers: First, compare the whole number parts of the mixed numbers.
2. If Whole Numbers Differ: If the whole numbers are different, the mixed number with the larger whole number is the larger mixed number.
3. If Whole Numbers are the Same: If the whole numbers are the same, compare the fractional parts using any of the methods described above.

For example, to compare 3 1/4 and 2 3/4:

• Compare the whole numbers: 3 and 2.
• Since 3 is greater than 2, 3 1/4 is larger than 2 3/4.

Now, consider comparing 2 1/4 and 2 3/4:

• Compare the whole numbers: Both are 2, so they are the same.
• Compare the fractional parts: 1/4 and 3/4.
• Since 3/4 is larger than 1/4, 2 3/4 is larger than 2 1/4.

3.2.2 Examples of Mixed Number Comparisons

Let’s look at additional examples:

• Example 1: Compare 4 1/2 and 4 2/5.
  • Compare the whole numbers: Both are 4, so they are the same.
  • Compare the fractional parts: 1/2 and 2/5.
  • Using cross multiplication: 1 5 = 5 and 2 2 = 4. So, 1/2 is larger than 2/5.
  • Therefore, 4 1/2 is larger than 4 2/5.
• Example 2: Compare 5 2/3 and 5 3/4.
  • Compare the whole numbers: Both are 5, so they are the same.
  • Compare the fractional parts: 2/3 and 3/4.
  • Using cross multiplication: 2 4 = 8 and 3 3 = 9. So, 3/4 is larger than 2/3.
  • Therefore, 5 3/4 is larger than 5 2/3.
• Example 3: Compare 1 7/8 and 2 1/4.
  • Compare the whole numbers: 1 and 2.
  • Since 2 is greater than 1, 2 1/4 is larger than 1 7/8.

3.3 Comparing Improper Fractions

An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 5/3). To compare improper fractions, you can convert them to mixed numbers and then compare the mixed numbers as described above, or you can use other comparison methods directly.

3.3.1 Method 1: Converting to Mixed Numbers

1. Convert to Mixed Numbers: Convert each improper fraction to a mixed number.
2. Compare Mixed Numbers: Compare the mixed numbers as described above (compare whole numbers first, then fractional parts if necessary).

For example, to compare 5/3 and 7/4:

• Convert 5/3 to a mixed number: 5 ÷ 3 = 1 with a remainder of 2, so 5/3 = 1 2/3.
• Convert 7/4 to a mixed number: 7 ÷ 4 = 1 with a remainder of 3, so 7/4 = 1 3/4.
• Compare the mixed numbers: 1 2/3 and 1 3/4.
• The whole numbers are the same, so compare the fractional parts: 2/3 and 3/4.
• Using cross multiplication: 2 4 = 8 and 3 3 = 9. So, 3/4 is larger than 2/3.
• Therefore, 7/4 is larger than 5/3.

3.3.2 Method 2: Using Common Denominators or Cross Multiplication Directly

If you prefer not to convert to mixed numbers, you can use the common denominator or cross-multiplication methods directly on the improper fractions.

For example, to compare 5/3 and 7/4 using cross multiplication:

• Cross multiply: 5 4 = 20 and 7 3 = 21.
• Since 21 is greater than 20, 7/4 is larger than 5/3.

3.3.3 Examples of Improper Fraction Comparisons

Let’s consider additional examples:

• Example 1: Compare 9/5 and 7/3.
  • Convert to mixed numbers: 9/5 = 1 4/5 and 7/3 = 2 1/3.
  • Compare the whole numbers: 1 and 2.
  • Since 2 is greater than 1, 7/3 is larger than 9/5.
• Example 2: Compare 11/4 and 13/5.
  • Convert to mixed numbers: 11/4 = 2 3/4 and 13/5 = 2 3/5.
  • The whole numbers are the same, so compare the fractional parts: 3/4 and 3/5.
  • Using cross multiplication: 3 5 = 15 and 3 4 = 12. So, 3/4 is larger than 3/5.
  • Therefore, 11/4 is larger than 13/5.
• Example 3: Compare 8/3 and 10/4.
  • Use cross multiplication directly: 8 4 = 32 and 10 3 = 30.
  • Since 32 is greater than 30, 8/3 is larger than 10/4.

4. Practical Applications and Real-World Examples

Understanding how to compare 2 fractions isn’t just a mathematical exercise; it’s a practical skill that’s useful in various real-world scenarios. Here are some examples:

• Cooking: When adjusting recipes, you often need to compare fractions of ingredients. For example, if a recipe calls for 2/3 cup of flour and you want to make a half batch, you need to know that half of 2/3 is 1/3.
• Shopping: Comparing discounts expressed as fractions can help you determine which deal is better. For example, a 1/4 off discount compared to a 1/5 off discount.
• Finance: Comparing investment returns or loan interest rates, which may be expressed as fractions or percentages, helps you make informed financial decisions.
• Construction: Measuring materials and planning layouts often involve fractions. Knowing how to compare them ensures accurate cuts and fits.

5. Tips and Tricks for Mastering Fraction Comparisons

Here are some additional tips and tricks to help you master fraction comparisons:

• Simplify Fractions: Always simplify fractions to their lowest terms before comparing them. This makes the numbers smaller and easier to work with.
• Use Benchmarks: Compare fractions to benchmarks like 0, 1/2, and 1 to get a quick sense of their size.
• Practice Regularly: The more you practice, the more comfortable you’ll become with comparing fractions.
• Understand the “Why”: Don’t just memorize the rules; understand why they work. This will help you apply them in different situations.
• Use Online Tools: There are many online tools and calculators that can help you compare fractions. These can be useful for checking your work or for quickly comparing complex fractions.

6. Common Mistakes to Avoid

When learning how to compare 2 fractions, it’s common to make mistakes. Here are some common pitfalls to avoid:

• Forgetting to Find a Common Denominator: You can’t directly compare fractions with different denominators without first finding a common denominator.
• Incorrectly Finding the LCM: Make sure you accurately calculate the least common multiple. A mistake here will lead to an incorrect comparison.
• Ignoring Negative Signs: When comparing negative fractions, remember to account for the negative signs and reverse the comparison if necessary.
• Not Simplifying Fractions: Failing to simplify fractions can make the comparison more difficult and increase the chance of error.
• Rushing the Process: Take your time and carefully follow the steps. Rushing can lead to careless mistakes.

7. Advanced Fraction Concepts

Once you’ve mastered the basics of comparing fractions, you can explore more advanced concepts:

• Ordering Fractions: Arranging a set of fractions from smallest to largest or vice versa.
• Fractions and Ratios: Understanding the relationship between fractions and ratios and how to compare ratios.
• Complex Fractions: Fractions within fractions, which require additional steps to simplify and compare.
• Fractions in Algebra: Using fractions in algebraic equations and expressions.

8. The Role of COMPARE.EDU.VN in Fraction Comparisons

COMPARE.EDU.VN is an invaluable resource for anyone looking to master the art of how to compare 2 fractions. Our platform offers detailed, step-by-step guides, interactive tools, and real-world examples that simplify the learning process. Whether you’re a student struggling with homework, a professional needing to make quick comparisons, or simply someone looking to brush up on their math skills, COMPARE.EDU.VN provides the resources you need to succeed.

8.1 Features of COMPARE.EDU.VN

• Comprehensive Guides: Step-by-step instructions on all methods of comparing fractions.
• Interactive Tools: Online calculators and visual aids to help you compare fractions quickly and accurately.
• Real-World Examples: Practical applications of fraction comparisons in everyday situations.
• Expert Insights: Tips and tricks from experienced educators and mathematicians.
• Practice Problems: A wide range of practice problems to test your skills and reinforce your learning.

By leveraging the resources available at COMPARE.EDU.VN, you can gain a deeper understanding of fraction comparisons and improve your overall math proficiency.

9. Conclusion: Mastering Fraction Comparisons

Comparing fractions is a fundamental skill that’s essential for success in mathematics and various real-world applications. By understanding the different methods for comparing fractions, avoiding common mistakes, and practicing regularly, you can master this skill and enhance your number sense.

Remember, the key to success is understanding the “why” behind the methods and taking your time to carefully follow the steps. And don’t forget to leverage the resources available at COMPARE.EDU.VN to support your learning journey.

10. Frequently Asked Questions (FAQs) About Comparing Fractions

10.1 What does comparing fractions mean?

Comparing fractions means determining which fraction has a greater value or if two fractions are equal. It involves assessing the relative sizes of the fractions to establish their relationship.

10.2 What is the rule for comparing fractions with the same denominator?

When fractions have the same denominator, the fraction with the larger numerator is the larger fraction. For example, in comparing 3/7 and 5/7, since 5 is greater than 3, 5/7 is the larger fraction.

10.3 How do you compare fractions with different denominators?

To compare fractions with different denominators, you must first find a common denominator, typically the least common multiple (LCM) of the denominators. Convert each fraction to an equivalent fraction with the common denominator and then compare the numerators.

10.4 What is the rule when comparing fractions with the same numerator?

When fractions have the same numerator, the fraction with the smaller denominator is the larger fraction. For example, in comparing 1/3 and 1/5, since 3 is smaller than 5, 1/3 is the larger fraction.

10.5 What are equivalent fractions?

Equivalent fractions are fractions that represent the same value but have different numerators and denominators. For example, 1/2 and 2/4 are equivalent fractions because they both equal 0.5.

10.6 What is the easiest way to compare fractions?

The easiest way to compare fractions is often to convert them into decimals by dividing the numerator by the denominator. Then, simply compare the decimal values.

10.7 Why do we need to compare fractions?

Comparing fractions is essential in various real-life scenarios, such as cooking, finance, construction, and education. It helps us make informed decisions based on accurate proportions and measurements.

10.8 How can visualization help in comparing fractions?

Visualizing fractions using diagrams like fraction bars or circles can make it easier to understand their relative sizes. By visually comparing the shaded areas representing different fractions, you can determine which fraction is larger.

10.9 What is cross multiplication and how does it help in comparing fractions?

Cross multiplication is a method where you multiply the numerator of one fraction by the denominator of the other fraction. By comparing the resulting products, you can determine which fraction is larger.

10.10 What should I do if I encounter negative fractions when comparing?

When comparing negative fractions, remember that the fraction with the smaller absolute value is the larger fraction (closer to zero). Ignore the negative signs, compare the absolute values, and then reverse the comparison.

Ready to take your fraction comparison skills to the next level? Visit compare.edu.vn today for more detailed guides, interactive tools, and expert tips. Make smarter decisions with confidence! Our address is 333 Comparison Plaza, Choice City, CA 90210, United States. You can also reach us on WhatsApp at +1 (626) 555-9090. Don’t wait – start comparing and conquering fractions now!