Comparing similar triangles involves understanding their properties and theorems. At COMPARE.EDU.VN, we offer detailed comparisons to help you master this concept and make informed decisions. This guide provides the essential knowledge and techniques for effectively comparing similar triangles, including practical examples and theorems. Unlock clarity and precision in your geometric analyses with a comparison of corresponding angles, proportional sides, and similarity criteria.
1. What Are Similar Triangles?
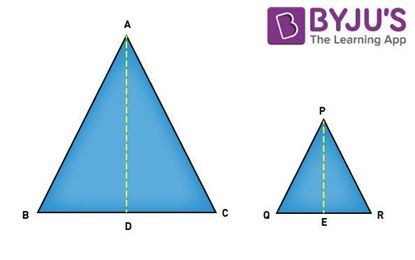
Similar triangles are triangles that share the same shape but can differ in size. This means their corresponding angles are congruent, and their corresponding sides are in proportion. Understanding this concept is crucial for various applications in geometry and beyond.
2. Defining Similarity
Two triangles are deemed similar if they meet specific criteria:
- Corresponding Angles: All pairs of corresponding angles are equal.
- Proportional Sides: The ratio of corresponding sides is constant.
In simpler terms, similar figures maintain the same shape, although their sizes may differ.
3. Examples of Similar Figures
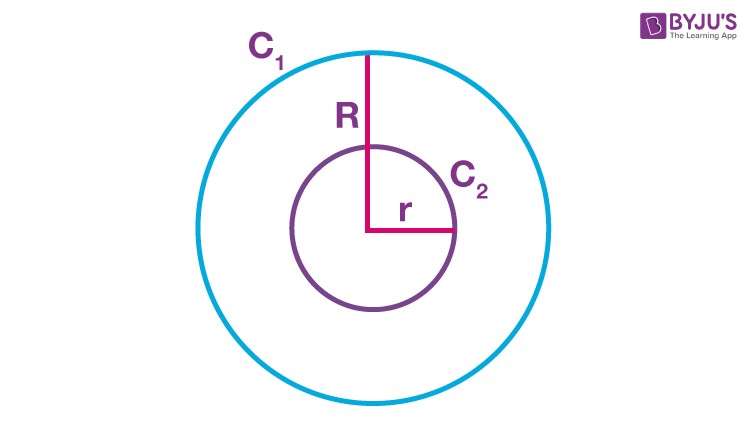
Consider everyday objects like hula hoops and bicycle wheels. Despite their different sizes, they share the same circular shape, making them similar figures.
4. Circles and Similarity
Circles, regardless of their diameter, always possess the same shape. Consequently, any two circles are always similar. This is a fundamental property in geometry.
5. Conditions for Triangle Similarity
For triangles, the conditions for similarity are more specific:
- Equal Corresponding Angles: All corresponding angles of the triangles must be equal.
- Proportional Corresponding Sides: The ratio of corresponding sides must be the same for all pairs of sides.
6. Example: Identifying Similar Triangles
Consider triangles ΔABC and ΔXYZ. They are similar if:
- ∠A = ∠X, ∠B = ∠Y, and ∠C = ∠Z (Equal corresponding angles)
- AB/XY = BC/YZ = AC/XZ (Proportional sides)
If these conditions are met, then ΔABC ~ ΔXYZ.
7. Equiangular Triangles
Triangles with equal corresponding angles are known as equiangular triangles. For such triangles, the Basic Proportionality Theorem (Thales Theorem) states:
- The ratio of any two corresponding sides in equiangular triangles is always the same.
8. Key Properties of Similar Triangles
- Shape: Maintain the same shape.
- Size: Sizes may differ.
- Angles: Each pair of corresponding angles are equal.
- Sides: The ratio of corresponding sides is constant.
9. Formulas for Similar Triangles
If triangles ABC and XYZ are similar, you can use these formulas to find missing dimensions:
- ∠A = ∠X, ∠B = ∠Y, and ∠C = ∠Z (Equal angles)
- AB/XY = BC/YZ = AC/XZ (Proportional sides)
10. Area of Similar Triangles
Once you know the dimensions and angles, calculating the area of similar triangles becomes straightforward. The ratio of their areas is the square of the ratio of their corresponding sides.
11. Similar vs. Congruent Triangles: A Comparison
| Feature | Similar Triangles | Congruent Triangles |
|---|---|---|
| Shape | Same shape, different size | Same shape and size |
| Symbol | ~ | ≅ |
| Ratio of Sides | Same ratio for corresponding sides | Ratio of corresponding sides equals a constant |
| Corresponding Angles | Corresponding angles are equal | Corresponding angles are equal |
| Side Lengths | Side lengths are proportional | Side lengths are equal |
| Area | Areas are proportional to the square of sides | Areas are equal |
12. Similar Triangles Theorems with Proofs
Several theorems help determine if triangles are similar. Let’s explore them with proofs.
13. AA (or AAA) or Angle-Angle Similarity
Theorem: If two angles of one triangle are equal to two angles of another triangle, the triangles are similar.
Explanation:
- If ∠A = ∠X and ∠C = ∠Z, then ΔABC ~ ΔXYZ.
- From this, we can conclude that AB/XY = BC/YZ = AC/XZ and ∠B = ∠Y.
14. Proof of AA Similarity
Consider two triangles, ABC and XYZ, where ∠A = ∠X and ∠B = ∠Y. We need to prove that ΔABC ~ ΔXYZ.
- Given: ∠A = ∠X and ∠B = ∠Y
- Third Angle: Since the sum of angles in a triangle is 180°, ∠C = 180° – (∠A + ∠B) and ∠Z = 180° – (∠X + ∠Y). Therefore, ∠C = ∠Z.
- Similarity: By the AAA (Angle-Angle-Angle) similarity criterion, if all three angles of one triangle are equal to the corresponding angles of another triangle, the triangles are similar. Hence, ΔABC ~ ΔXYZ.
15. SAS or Side-Angle-Side Similarity
Theorem: If two sides of one triangle are proportional to two sides of another triangle, and the included angles are equal, the triangles are similar.
Explanation:
- If ∠A = ∠X and AB/XY = AC/XZ, then ΔABC ~ ΔXYZ.
- From this congruency, AB/XY = BC/YZ = AC/XZ, and ∠B = ∠Y and ∠C = ∠Z.
16. Proof of SAS Similarity
Consider triangles ABC and XYZ, where AB/XY = AC/XZ and ∠A = ∠X. We aim to prove that ΔABC ~ ΔXYZ.
- Given: AB/XY = AC/XZ and ∠A = ∠X
- Construction: On XY, mark a point P such that XP = AB. On XZ, mark a point Q such that XQ = AC.
- Similarity:
- Since AB/XY = AC/XZ, and XP = AB, XQ = AC, we have XP/XY = XQ/XZ.
- By the converse of the Basic Proportionality Theorem, PQ || YZ.
- Therefore, ∠XPQ = ∠Y and ∠XQP = ∠Z.
- Thus, ΔXPQ ~ ΔXYZ.
- Congruence: Since XP = AB, XQ = AC, and ∠X = ∠A, ΔXPQ ≅ ΔABC by SAS congruence.
- Conclusion: Therefore, ΔABC ~ ΔXYZ.
17. SSS or Side-Side-Side Similarity
Theorem: If all three sides of one triangle are proportional to the three sides of another triangle, then the two triangles are similar.
Explanation:
- If AB/XY = BC/YZ = AC/XZ, then ΔABC ~ ΔXYZ.
- From this, we can infer that ∠A = ∠X, ∠B = ∠Y, and ∠C = ∠Z.
18. Proof of SSS Similarity
Given two triangles, ABC and XYZ, where AB/XY = BC/YZ = AC/XZ, we want to show that ΔABC ~ ΔXYZ.
- Given: AB/XY = BC/YZ = AC/XZ.
- Construction: Choose points P and Q on XY and XZ, respectively, such that XP = AB and XQ = AC.
- Proportionality: From the given ratios, XP/XY = XQ/XZ. Therefore, PQ || YZ.
- AAA Similarity: This implies that ∠XPQ = ∠Y and ∠XQP = ∠Z. Hence, ΔXPQ ~ ΔXYZ by AAA similarity.
- Side Lengths: Since AB/XY = BC/YZ = AC/XZ and XP = AB, XQ = AC, we deduce that PQ/YZ = AB/XY. Thus, PQ = BC.
- Congruence: By SSS congruence, ΔABC ≅ ΔXPQ.
- Conclusion: Therefore, ΔABC ~ ΔXYZ.
19. Problem and Solutions
Let’s solve some problems to reinforce your understanding.
20. Problem 1: Finding a Side Length
Q: In ΔABC, AP = 5 cm, PB = 10 cm, BC = 20 cm, and PQ || BC. Find PQ.
Solution:
- Identify Similar Triangles: ΔABC ~ ΔAPQ by the AA criterion (∠PAQ is common, and ∠APQ = ∠ABC).
- Set up Proportion: AP/AB = PQ/BC
- Substitute Values: 5/15 = PQ/20
- Solve for PQ: PQ = 20/3 cm
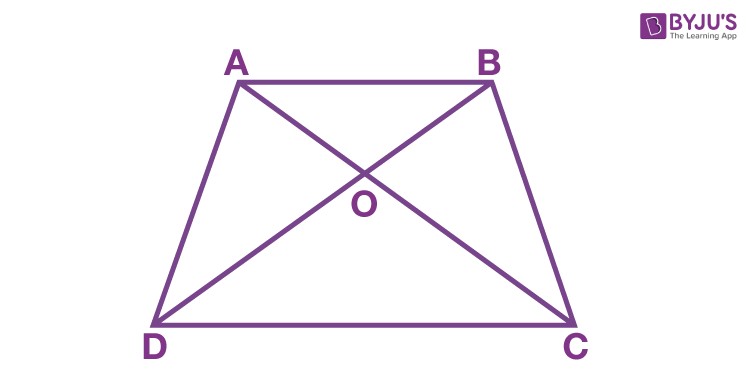
21. Problem 2: Proving a Proportion
Q: Diagonals AC and BD of trapezium ABCD (AB || DC) intersect at O. Show that AO/OC = OB/OD using similarity.
Solution:
- Identify Similar Triangles: In ΔDOC and ΔBOA, ∠CDO = ∠ABO (alternate interior angles), and ∠DCO = ∠BAO.
- AAA Similarity: By AAA criterion, ΔDOC ~ ΔBOA.
- Set up Proportion: DO/BO = OC/OA
- Rearrange: OA/OC = OB/OD (Hence, proved)
22. Problem 3: Checking for Similarity
Q: Determine if triangles PQR and XYZ are similar given their angles.
Solution:
- Find Missing Angles:
- In ΔPQR, ∠R = 180° – (60° + 70°) = 50°
- In ΔXYZ, ∠Y = 180° – (60° + 50°) = 70°
- Compare Angles: ∠Q = ∠Y = 70° and ∠Z = ∠R = 50°
- Conclusion: By the Angle-Angle (AA) rule, ΔPQR ~ ΔXYZ.
23. Frequently Asked Questions – FAQs
Q1: What are similar triangles?
Similar triangles are triangles that have the same shape but can be of different sizes. Their corresponding angles are equal, and their corresponding sides are in proportion.
Q2: What is the symbol for similar triangles?
The symbol used to denote that two triangles, say ABC and PQR, are similar is ∆ABC ~ ∆PQR.
Q3: Are similar triangles and congruent triangles the same?
No, similar triangles have the same shape but may have different sizes, whereas congruent triangles have the same shape and size. Congruent triangles are represented by the symbol ‘≅’.
Q4: What are three similarities theorems for triangles?
The three similarity theorems for triangles are:
- Angle-Angle (AA)
- Side-Angle-Side (SAS)
- Side-Side-Side (SSS)
Q5: How to find the proportion of similar triangles?
If two triangles are similar and have sides A, B, C and a, b, c, respectively, then the pair of corresponding sides are proportional, i.e., A : a = B : b = C : c.
24. Real-World Applications of Similar Triangles
- Architecture: Architects use similar triangles to create scaled models of buildings.
- Navigation: Sailors use similar triangles to determine distances to landmarks.
- Photography: Photographers use similar triangles to adjust focus and perspective.
- Engineering: Engineers use similar triangles in structural design and surveying.
- Cartography: Mapmakers rely on similar triangles to create accurate maps.
- Astronomy: Astronomers use similar triangles to measure distances to celestial objects.
- Art: Artists use similar triangles to create perspective in their paintings.
25. Advanced Concepts in Similarity
- Fractals: Similar triangles play a key role in the creation of fractals. Fractals are infinitely complex patterns that exhibit self-similarity at different scales.
- Homothety: Homothety is a transformation that scales an object with respect to a fixed point. Similar triangles are the basis for understanding homothety.
- Projective Geometry: Similar triangles are crucial in projective geometry, where parallel lines are considered to meet at infinity.
- Computer Graphics: Similar triangles are used in 3D modeling and rendering to create realistic images.
- Physics: Similar triangles are used in optics to analyze the behavior of light.
26. The Importance of Clear Comparisons
Understanding and comparing similar triangles correctly can significantly improve your problem-solving skills in geometry and related fields. By recognizing the properties and theorems associated with similar triangles, you can approach complex problems with confidence and accuracy.
27. Need More Help?
At COMPARE.EDU.VN, we understand the challenges in comparing complex mathematical concepts. That’s why we offer detailed, unbiased comparisons to help you make informed decisions. Whether you’re a student, a professional, or just curious, our resources are designed to clarify and simplify.
28. Make Informed Decisions with COMPARE.EDU.VN
Do you find it challenging to compare different geometric shapes or theorems? Visit COMPARE.EDU.VN for comprehensive comparisons that highlight the pros, cons, and key features of each. Our detailed analysis helps you make informed decisions, saving you time and effort.
29. Ready to Explore More?
Take the next step in mastering geometry. Visit COMPARE.EDU.VN today to explore our extensive collection of comparisons and educational resources. Empower yourself with the knowledge you need to excel.
30. Contact Us
Have questions or need personalized assistance? Reach out to us!
- Address: 333 Comparison Plaza, Choice City, CA 90210, United States
- WhatsApp: +1 (626) 555-9090
- Website: COMPARE.EDU.VN
Let compare.edu.vn be your guide to clarity and informed decision-making in the world of geometry and beyond.
