How Do You Compare 3 Ratios? A Simple Guide

Comparing three or more ratios can seem daunting, but it’s actually a straightforward process. At COMPARE.EDU.VN, we simplify complex comparisons, and this guide shows you exactly how to do it. Master ratio comparisons and make informed decisions with our easy-to-follow methods. Unlock the power of ratio comparisons!

1. Understanding Ratios and Their Importance

Before diving into the “how,” it’s crucial to understand the “what” and “why.” A ratio is a comparison of two quantities, indicating how much of one thing there is compared to another. They are fundamental in various fields, from cooking and finance to science and engineering.

Definition: A ratio expresses the relative sizes of two or more values. It can be written in several ways: as a fraction (a/b), with a colon (a:b), or using the word “to” (a to b).
Real-World Applications: Ratios are everywhere. In cooking, a recipe might call for a 2:1 ratio of water to rice. In finance, debt-to-equity ratios are used to assess a company’s financial leverage. In science, ratios are used to express concentrations, proportions, and scales.
Why Compare Ratios? Comparing ratios becomes essential when you need to evaluate different proportions or relationships. For instance, you might want to compare the fuel efficiency of three different cars (miles per gallon) or assess the profitability of several investment options (return on investment).
Benefits of Accurate Comparison: Accurate ratio comparison leads to informed decision-making. Whether you’re a student comparing study time allocation, a consumer evaluating product value, or a business professional analyzing performance metrics, understanding how to compare ratios effectively is invaluable.
Common Mistakes to Avoid: A common mistake is comparing ratios without ensuring they are in the same units or context. For example, comparing a ratio of miles to gallons with a ratio of kilometers to liters directly would be misleading. Always standardize units and consider the underlying context.

2. Identifying Your Search Intent

Understanding why someone searches for “How To Compare 3 Ratios” is key to providing the right information. Here are five common search intents:

Method Exploration: Users want to learn the specific methods for comparing ratios, such as finding a common denominator or using cross-multiplication.
Practical Application: Users need to apply ratio comparison to real-world problems, like comparing prices, mixtures, or performance metrics.
Conceptual Understanding: Users seek a clearer understanding of what ratios are and why comparing them is useful.
Step-by-Step Guidance: Users require detailed, step-by-step instructions on how to compare ratios, often with examples.
Verification and Confirmation: Users want to confirm their understanding of the methods and ensure they are applying them correctly.

3. Core Methods for Comparing Ratios

There are several established methods for comparing ratios, each with its own strengths and applications. We will explore the two most common and versatile methods: finding a common denominator and using cross-multiplication.

3.1. Method 1: Finding a Common Denominator

This method is based on the principle that fractions can be easily compared when they have the same denominator. By converting ratios into fractions and finding a common denominator, you can directly compare their numerators.

Step-by-Step Instructions:
1. Convert Ratios to Fractions: Express each ratio as a fraction. For example, the ratio a:b becomes a/b.
2. Find the Least Common Multiple (LCM): Determine the LCM of all the denominators. The LCM is the smallest number that is a multiple of all the denominators.
3. Convert Fractions: Convert each fraction to an equivalent fraction with the LCM as the denominator. To do this, multiply both the numerator and denominator of each fraction by the factor that makes the denominator equal to the LCM.
4. Compare Numerators: Once all fractions have the same denominator, compare their numerators. The fraction with the largest numerator represents the largest ratio.
Example:

Compare the ratios 2:3, 3:4, and 5:6.
1. Convert to Fractions: 2/3, 3/4, 5/6
2. Find LCM: The LCM of 3, 4, and 6 is 12.
3. Convert Fractions:
  - 2/3 = (2*4)/(3*4) = 8/12
  - 3/4 = (3*3)/(4*3) = 9/12
  - 5/6 = (5*2)/(6*2) = 10/12
4. Compare Numerators: 8/12, 9/12, 10/12. Since 10 > 9 > 8, the ratio 5:6 is the largest, followed by 3:4, and then 2:3.
When to Use This Method: This method is particularly useful when you have several ratios to compare and when you are comfortable working with fractions.
Advantages: It provides a clear visual comparison and is easy to understand.
Disadvantages: Finding the LCM can be time-consuming with larger numbers.

3.2. Method 2: Cross-Multiplication

Cross-multiplication is a quick method for comparing two ratios at a time. It involves multiplying the numerator of one ratio by the denominator of the other and vice versa.

Step-by-Step Instructions:
1. Choose Two Ratios: Select any two ratios to compare.
2. Convert to Fractions: Express each ratio as a fraction.
3. Cross-Multiply: Multiply the numerator of the first fraction by the denominator of the second fraction. Then, multiply the numerator of the second fraction by the denominator of the first fraction.
4. Compare the Products: Compare the two products. If the first product is greater, the first ratio is larger. If the second product is greater, the second ratio is larger. If the products are equal, the ratios are equal.
5. Repeat: Repeat the process with another pair of ratios until all ratios have been compared.
Example:

Compare the ratios 3:5, 4:7, and 2:3.
1. Compare 3:5 and 4:7:
  - Convert to Fractions: 3/5 and 4/7
  - Cross-Multiply: 3*7 = 21 and 4*5 = 20
  - Compare: Since 21 > 20, 3:5 > 4:7
2. Compare 3:5 and 2:3:
  - Convert to Fractions: 3/5 and 2/3
  - Cross-Multiply: 3*3 = 9 and 2*5 = 10
  - Compare: Since 10 > 9, 2:3 > 3:5
3. Conclusion: Combining the results, we find that 2:3 > 3:5 > 4:7.
When to Use This Method: This method is ideal for quickly comparing pairs of ratios, especially when dealing with relatively small numbers.
Advantages: It is fast and straightforward, requiring minimal calculations.
Disadvantages: It can become cumbersome when comparing many ratios, as it requires multiple comparisons.

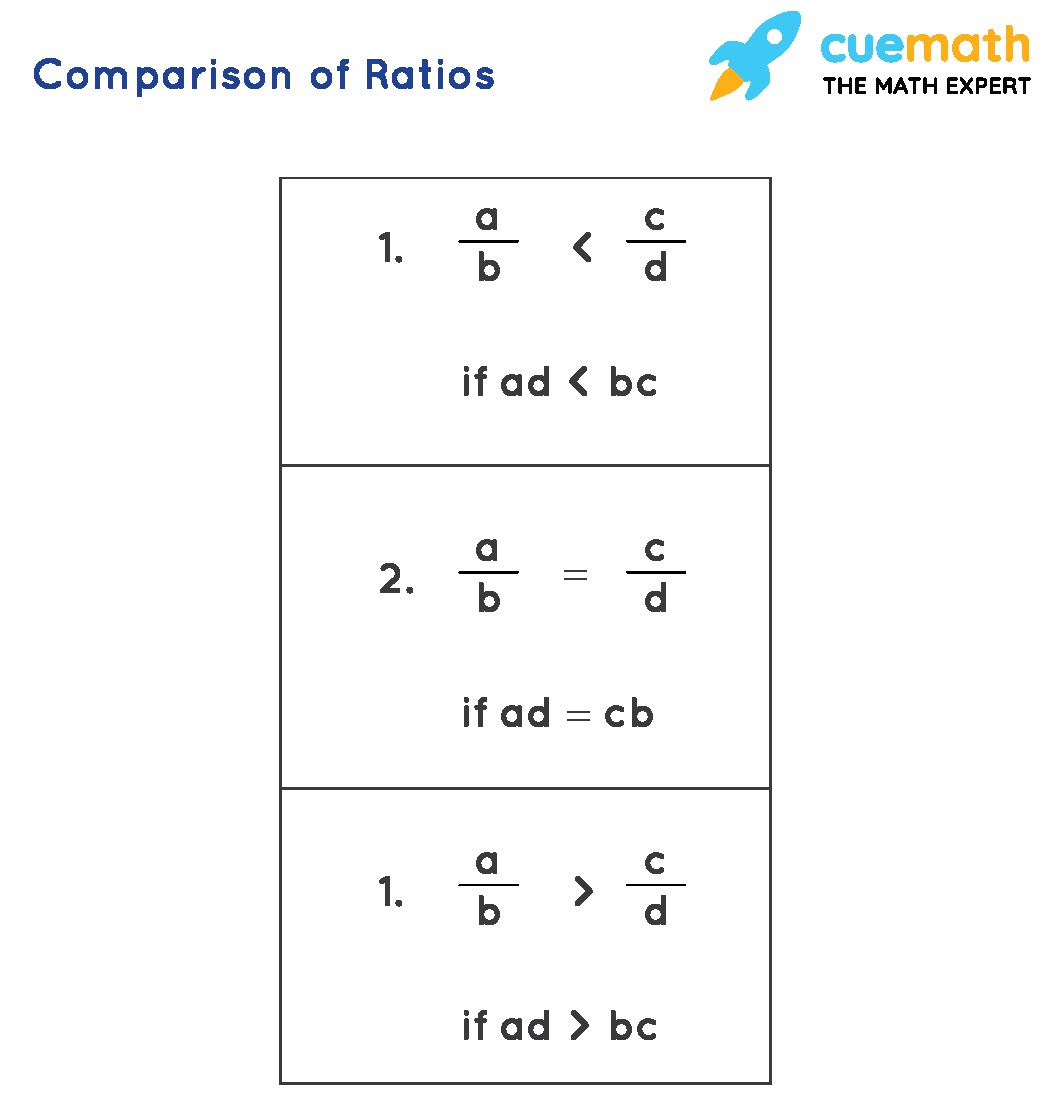Cross Multiplication Method

4. Advanced Techniques and Considerations

While the common denominator and cross-multiplication methods are effective, there are situations where more advanced techniques are necessary.

4.1. Using Proportions to Simplify Comparisons

Proportions are statements that two ratios are equal. Understanding and using proportions can simplify complex comparisons.

Definition of Proportion: A proportion is an equation stating that two ratios are equal. For example, if a/b = c/d, then the ratios a:b and c:d are in proportion.
Setting Up Proportions: When comparing ratios, you can set up proportions to find unknown quantities or to simplify comparisons. For instance, if you know that two mixtures should have the same ratio of ingredients, you can use a proportion to determine the amount of one ingredient needed in the second mixture.
Solving for Unknowns: Proportions can be solved using cross-multiplication. If a/b = c/x, then ax = bc, and x = (bc)/a.
Example:

Suppose you have two mixtures. The first mixture has a ratio of 2:5 of ingredient A to ingredient B and contains 10 grams of ingredient B. The second mixture should have the same ratio but contains 8 grams of ingredient B. How much of ingredient A is needed in the second mixture?
- Set up the proportion: 2/5 = x/8
- Solve for x: 5x = 2*8, so x = 16/5 = 3.2 grams
- Therefore, you need 3.2 grams of ingredient A in the second mixture.

4.2. Dealing with More Than Three Ratios

When comparing more than three ratios, the common denominator method becomes particularly useful. However, there are strategies to streamline the process.

Grouping and Comparing: Divide the ratios into smaller groups and compare them using the common denominator or cross-multiplication methods. Then, compare the results of these smaller groups to determine the overall order.
Using a Spreadsheet: For a large number of ratios, using a spreadsheet can automate the calculations and make the comparison process more efficient.
Standardizing Ratios: Convert all ratios to a standard form, such as percentages or decimals, to make comparisons easier.

4.3. Handling Ratios with Different Units

One of the most common pitfalls in comparing ratios is failing to account for different units. Always ensure that the quantities being compared are in the same units.

Importance of Unit Conversion: Comparing ratios with different units is like comparing apples and oranges. You must convert all quantities to the same unit before making a comparison.
Common Unit Conversions: Familiarize yourself with common unit conversions, such as converting between meters and feet, kilograms and pounds, or liters and gallons.
Example:

Compare the speeds of two cars: Car A travels 120 miles in 3 hours, and Car B travels 200 kilometers in 4 hours.
- Convert kilometers to miles: 200 kilometers ≈ 124.27 miles
- Calculate the speeds:
  - Car A: 120 miles / 3 hours = 40 mph
  - Car B: 124.27 miles / 4 hours = 31.07 mph
- Compare: Car A is faster than Car B.

5. Real-World Examples and Applications

To solidify your understanding, let’s look at some real-world examples where comparing ratios is essential.

5.1. Comparing Investment Options

When evaluating investment options, ratios like return on investment (ROI) and risk-reward ratio are crucial.

ROI Calculation: ROI = (Net Profit / Cost of Investment) * 100%
Risk-Reward Ratio: Risk-Reward Ratio = (Potential Loss / Potential Gain)
Example:

Consider two investment options:
- Investment A: Costs $10,000 and is expected to generate a net profit of $1,500.
- Investment B: Costs $15,000 and is expected to generate a net profit of $2,000.
Calculate the ROI for each:
- Investment A: ($1,500 / $10,000) * 100% = 15%
- Investment B: ($2,000 / $15,000) * 100% = 13.33%
- Compare: Investment A has a higher ROI than Investment B.

5.2. Analyzing Financial Ratios

Financial ratios are used to assess a company’s financial health and performance. Common ratios include debt-to-equity, current ratio, and profit margin.

Debt-to-Equity Ratio: Debt-to-Equity = (Total Debt / Total Equity)
Current Ratio: Current Ratio = (Current Assets / Current Liabilities)
Profit Margin: Profit Margin = (Net Income / Revenue) * 100%
Example:

Compare two companies:
- Company X: Total Debt = $500,000, Total Equity = $1,000,000
- Company Y: Total Debt = $750,000, Total Equity = $900,000
Calculate the Debt-to-Equity Ratio for each:
- Company X: $500,000 / $1,000,000 = 0.5
- Company Y: $750,000 / $900,000 ≈ 0.83
- Compare: Company X has a lower Debt-to-Equity Ratio, indicating it is less leveraged than Company Y.

5.3. Comparing Product Value

When shopping, comparing ratios like price-to-quality or value-for-money can help you make informed purchasing decisions.

Price-to-Quality Ratio: Evaluate the price of a product relative to its quality or features.
Value-for-Money: Assess whether the benefits and features of a product justify its cost.
Example:

Consider two smartphones:
- Phone A: Costs $600 and has a 4.5-star rating from 500 reviews.
- Phone B: Costs $800 and has a 4.7-star rating from 750 reviews.
Calculate the Price-to-Quality Ratio (assuming a higher rating indicates better quality):
- Phone A: $600 / 4.5 = $133.33 per rating point
- Phone B: $800 / 4.7 = $170.21 per rating point
- Compare: Phone A offers better value per rating point than Phone B.

5.4. Analyzing Scientific Data

In scientific research, ratios are used to compare experimental results, concentrations, and proportions.

Concentration Ratios: Compare the concentration of a substance in different solutions.
Proportion Ratios: Analyze the proportions of different elements in a compound.
Example:

Compare the concentration of a chemical in two solutions:
- Solution 1: Contains 20 grams of the chemical in 500 ml of water.
- Solution 2: Contains 30 grams of the chemical in 750 ml of water.
Calculate the concentration ratios:
- Solution 1: 20 grams / 500 ml = 0.04 grams/ml
- Solution 2: 30 grams / 750 ml = 0.04 grams/ml
- Compare: Both solutions have the same concentration of the chemical.

6. Common Mistakes and How to Avoid Them

Even with a solid understanding of the methods, it’s easy to make mistakes when comparing ratios. Here are some common pitfalls and how to avoid them.

Incorrect Unit Conversion: Always double-check your unit conversions. Use reliable conversion factors and be consistent with your units.
Misinterpreting Ratios: Understand what the ratio represents in its context. A high ratio might be good in one situation but bad in another.
Ignoring Context: Consider the underlying factors that might influence the ratios. A seemingly better ratio might be misleading if you don’t understand the full picture.
Comparing Non-Comparable Ratios: Ensure that the ratios you are comparing are truly comparable. They should relate to the same quantities and be measured in the same way.

7. Tools and Resources for Ratio Comparison

Several tools and resources can help you compare ratios more efficiently and accurately.

Spreadsheet Software: Programs like Microsoft Excel and Google Sheets can automate calculations and provide visual representations of ratios.
Online Calculators: Many online calculators are specifically designed for ratio comparison, such as those found on websites like CalculatorSoup and MiniWebtool.
Statistical Software: For more advanced analysis, statistical software packages like R and SPSS offer a wide range of tools for comparing and analyzing ratios.
COMPARE.EDU.VN: Your one-stop platform for comprehensive comparisons, including detailed ratio analyses across various domains.

8. Optimizing Your Comparisons for Different Scenarios

The best approach to comparing ratios depends on the specific scenario. Here are some tips for optimizing your comparisons in different situations.

Simple Comparisons: For quick comparisons of two or three ratios, cross-multiplication is often the most efficient method.
Complex Comparisons: When comparing many ratios or dealing with complex data, the common denominator method and spreadsheet software are more suitable.
Academic Settings: In academic settings, focus on showing your work and explaining your reasoning clearly.
Professional Settings: In professional settings, prioritize accuracy and efficiency. Use appropriate tools and resources to ensure your comparisons are reliable.

9. Frequently Asked Questions (FAQs)

Here are some frequently asked questions about comparing ratios:

9.1. What is the easiest way to compare ratios?

The easiest way to compare two ratios is often the cross-multiplication method. It is quick and requires minimal calculations.

9.2. How do you compare three or more ratios?

For three or more ratios, the common denominator method is usually the most effective. Convert all ratios to fractions with a common denominator and then compare the numerators.

9.3. What should I do if the ratios have different units?

Always convert all quantities to the same unit before comparing ratios. Use reliable conversion factors and double-check your work.

9.4. Can I use a calculator to compare ratios?

Yes, calculators can be very helpful for comparing ratios. Many online calculators are specifically designed for this purpose.

9.5. What is the importance of understanding ratios in real life?

Understanding ratios is important in many areas of life, including cooking, finance, science, and engineering. It helps you make informed decisions and solve problems effectively.

9.6. How does COMPARE.EDU.VN help in comparing ratios?

COMPARE.EDU.VN provides comprehensive comparisons, including detailed ratio analyses across various domains, helping you make informed decisions quickly and easily.

9.7. What are some common mistakes to avoid when comparing ratios?

Common mistakes include incorrect unit conversion, misinterpreting ratios, ignoring context, and comparing non-comparable ratios.

9.8. How can I improve my understanding of ratios?

Practice comparing ratios in different scenarios, use online resources and tools, and seek feedback from others.

9.9. What is a proportion, and how does it relate to ratios?

A proportion is an equation stating that two ratios are equal. Proportions can be used to solve for unknown quantities or to simplify comparisons.

9.10. Where can I find more resources on comparing ratios?

You can find more resources on websites like Khan Academy, CalculatorSoup, and MiniWebtool, as well as on COMPARE.EDU.VN.

10. Conclusion: Mastering Ratio Comparison for Informed Decisions

Comparing ratios is a fundamental skill with wide-ranging applications. By understanding the core methods, avoiding common mistakes, and utilizing available tools, you can master ratio comparison and make informed decisions in various aspects of your life. At COMPARE.EDU.VN, we are committed to providing you with the resources and tools you need to make accurate and insightful comparisons.

Ready to make smarter decisions? Visit COMPARE.EDU.VN today to explore detailed comparisons and find the best options for your needs. Whether you’re evaluating investment opportunities, comparing product values, or analyzing scientific data, we’re here to help you make the right choice.

Address: 333 Comparison Plaza, Choice City, CA 90210, United States

Whatsapp: +1 (626) 555-9090

Website: compare.edu.vn