Comparing fractions can be simple and straightforward when you know the right methods. This comprehensive guide on compare.edu.vn breaks down various techniques to help you determine which fraction is larger or smaller, enhancing your understanding of numerical relationships. Discover practical tips and strategies, improve your fraction skills, and confidently apply these concepts in real-world scenarios with our comprehensive comparisons of fractions, simplifying your learning journey with valuable resources and insights into comparing fractions and fractional values.
1. What Does It Mean To Compare Fractions?
Comparing fractions involves determining the relative size of two or more fractions. Essentially, you are trying to figure out which fraction represents a larger or smaller portion of a whole. This process is fundamental in mathematics and is used in everyday situations, from cooking to measuring. Understanding how to compare fractions is crucial for various mathematical operations and problem-solving scenarios.
1.1 Why Is Comparing Fractions Important?
Comparing fractions is a fundamental skill with numerous applications in real life. Imagine you’re following a recipe that calls for 1/3 cup of sugar, but you only have a measuring cup for 1/4 cup. Knowing that 1/3 is greater than 1/4 allows you to estimate the amount correctly. In education, comparing fractions helps students develop a strong number sense and understand the relationship between different quantities. Whether it’s calculating proportions, understanding financial ratios, or solving complex mathematical problems, the ability to compare fractions accurately is invaluable.
1.2 Basic Terminology: Numerator and Denominator
Before diving into the methods of comparing fractions, it’s essential to understand the basic components of a fraction: the numerator and the denominator.
- Numerator: The number above the fraction bar, indicating how many parts of the whole are being considered.
- Denominator: The number below the fraction bar, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 3/4, 3 is the numerator, and 4 is the denominator. Understanding these terms is crucial for grasping the concepts of comparing fractions.
2. Comparing Fractions With The Same Denominator
When fractions share the same denominator, comparing them is straightforward. The fraction with the larger numerator is the larger fraction. This method simplifies the comparison process, making it easy to identify the greater or smaller fraction.
2.1 The Rule: Larger Numerator Means Larger Fraction
When comparing fractions with the same denominator, the rule is simple: the fraction with the larger numerator is the larger fraction. For example, when comparing 3/7 and 5/7, since both fractions have the same denominator (7), you only need to compare the numerators. Because 5 is greater than 3, 5/7 is greater than 3/7. This rule makes it easy to quickly determine which fraction represents a larger portion of the whole when the denominators are the same.
2.2 Examples Of Comparing Fractions With The Same Denominator
To illustrate this concept, consider the following examples:
- Example 1: Compare 2/9 and 6/9. Both fractions have the same denominator (9), so we compare the numerators. Since 6 is greater than 2, 6/9 > 2/9.
- Example 2: Compare 7/15 and 4/15. Again, the denominators are the same (15). Comparing the numerators, 7 is greater than 4, so 7/15 > 4/15.
- Example 3: Compare 11/20 and 13/20. With the same denominator (20), we compare the numerators. 13 is greater than 11, so 13/20 > 11/20.
These examples demonstrate how easy it is to compare fractions when they have the same denominator. You simply look at the numerators to determine which fraction is larger.
2.3 Practice Problems
Test your understanding with these practice problems:
- Compare 4/11 and 9/11.
- Compare 5/13 and 2/13.
- Compare 8/17 and 12/17.
Answers: 1. 9/11 > 4/11, 2. 5/13 > 2/13, 3. 12/17 > 8/17
3. Comparing Fractions With Different Denominators
Comparing fractions becomes more complex when the denominators are different. Several methods can be used to make this comparison, including finding a common denominator, using cross-multiplication, or converting fractions to decimals.
3.1 Method 1: Finding A Common Denominator
One of the most common methods for comparing fractions with different denominators is to find a common denominator. This involves finding a multiple that both denominators can divide into evenly, and then converting each fraction to have this common denominator. Once the denominators are the same, you can compare the numerators as before.
3.1.1 How To Find The Least Common Denominator (LCD)
The least common denominator (LCD) is the smallest multiple that both denominators can divide into. Here’s how to find it:
-
List the multiples of each denominator: For example, if you’re comparing 1/4 and 2/6:
- Multiples of 4: 4, 8, 12, 16, 20, 24, …
- Multiples of 6: 6, 12, 18, 24, 30, …
-
Identify the smallest multiple that appears in both lists: In this case, the smallest common multiple is 12. Therefore, the LCD of 4 and 6 is 12.
3.1.2 Converting Fractions To Have The LCD
Once you’ve found the LCD, you need to convert each fraction so that its denominator matches the LCD. To do this, multiply both the numerator and the denominator of each fraction by the factor that makes the original denominator equal to the LCD.
-
For 1/4: To convert the denominator 4 to 12, multiply by 3. So, multiply both the numerator and denominator by 3:
- (1 3) / (4 3) = 3/12
-
For 2/6: To convert the denominator 6 to 12, multiply by 2. So, multiply both the numerator and denominator by 2:
- (2 2) / (6 2) = 4/12
Now that both fractions have the same denominator, you can easily compare them. Since 4/12 is greater than 3/12, 2/6 is greater than 1/4.
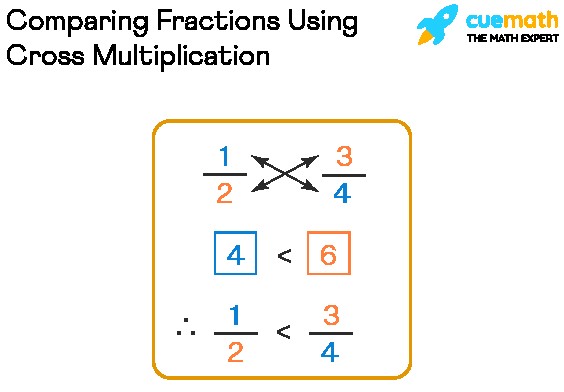
3.2 Method 2: Cross-Multiplication
Cross-multiplication is a quick method for comparing two fractions. It involves multiplying the numerator of one fraction by the denominator of the other, and then comparing the results.
3.2.1 How To Apply Cross-Multiplication
To compare two fractions using cross-multiplication:
-
Write down the two fractions you want to compare: For example, 3/5 and 2/3.
-
Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and multiply the numerator of the second fraction by the denominator of the first fraction.
- 3 (numerator of the first fraction) * 3 (denominator of the second fraction) = 9
- 2 (numerator of the second fraction) * 5 (denominator of the first fraction) = 10
-
Compare the results: The fraction that corresponds to the larger result is the larger fraction. In this case, 10 is greater than 9, so 2/3 is greater than 3/5.
3.2.2 Advantages And Disadvantages
- Advantages:
- It is a quick and straightforward method, especially useful when you only need to compare two fractions.
- It doesn’t require finding a common denominator, which can save time.
- Disadvantages:
- It only works for comparing two fractions at a time. If you have more than two fractions, you need to apply it multiple times.
- It doesn’t provide a clear sense of the actual size of the fractions, only their relative size.
3.3 Method 3: Converting Fractions To Decimals
Another method for comparing fractions is to convert them to decimals. This allows you to compare fractions using the familiar decimal system, making it easier to determine which fraction is larger.
3.3.1 How To Convert A Fraction To A Decimal
To convert a fraction to a decimal, divide the numerator by the denominator. For example:
-
Convert 3/4 to a decimal: Divide 3 by 4.
- 3 ÷ 4 = 0.75
-
Convert 5/8 to a decimal: Divide 5 by 8.
- 5 ÷ 8 = 0.625
3.3.2 Comparing Decimals
Once you have converted the fractions to decimals, comparing them is straightforward. Simply compare the decimal values to determine which fraction is larger. For example:
-
Compare 0.75 (which is 3/4) and 0.625 (which is 5/8).
- Since 0.75 is greater than 0.625, 3/4 is greater than 5/8.
Converting fractions to decimals is particularly useful when dealing with fractions that are difficult to compare directly or when you need a precise comparison.
3.4 Examples Of Comparing Fractions With Unlike Denominators
To illustrate these methods, let’s look at some examples:
-
Example 1: Compare 2/3 and 3/4 using the common denominator method.
- The LCD of 3 and 4 is 12.
- Convert 2/3 to 8/12 (multiply both numerator and denominator by 4).
- Convert 3/4 to 9/12 (multiply both numerator and denominator by 3).
- Since 9/12 > 8/12, 3/4 > 2/3.
-
Example 2: Compare 1/5 and 2/7 using cross-multiplication.
- 1 * 7 = 7
- 2 * 5 = 10
- Since 10 > 7, 2/7 > 1/5.
-
Example 3: Compare 3/8 and 5/12 by converting to decimals.
- 3/8 = 0.375
- 5/12 = 0.4167 (approximately)
- Since 0.4167 > 0.375, 5/12 > 3/8.
3.5 Practice Problems
Test your skills with these practice problems:
- Compare 2/5 and 3/7 using all three methods.
- Compare 1/3 and 3/10 using all three methods.
- Compare 4/9 and 5/11 using all three methods.
Answers: 1. 3/7 > 2/5, 2. 1/3 > 3/10, 3. 5/11 > 4/9
4. Comparing Mixed Numbers
Mixed numbers combine a whole number and a fraction (e.g., 2 1/2). Comparing mixed numbers involves comparing both the whole number part and the fractional part.
4.1 Comparing The Whole Number Part
The first step in comparing mixed numbers is to compare the whole number parts. If the whole numbers are different, the mixed number with the larger whole number is the larger mixed number.
-
Example: Compare 3 1/4 and 2 3/5.
- The whole number part of 3 1/4 is 3, and the whole number part of 2 3/5 is 2.
- Since 3 is greater than 2, 3 1/4 is greater than 2 3/5.
4.2 Comparing The Fractional Part (If Whole Numbers Are Equal)
If the whole number parts of the mixed numbers are equal, you need to compare the fractional parts. Use any of the methods discussed earlier (common denominator, cross-multiplication, or converting to decimals) to compare the fractions.
-
Example: Compare 4 2/5 and 4 3/7.
- Both mixed numbers have the same whole number part (4), so we need to compare the fractional parts 2/5 and 3/7.
- Using cross-multiplication:
- 2 * 7 = 14
- 3 * 5 = 15
- Since 15 > 14, 3/7 is greater than 2/5.
- Therefore, 4 3/7 is greater than 4 2/5.
4.3 Converting Mixed Numbers To Improper Fractions
Another method for comparing mixed numbers is to convert them to improper fractions. This involves multiplying the whole number by the denominator, adding the numerator, and placing the result over the original denominator.
4.3.1 How To Convert Mixed Numbers To Improper Fractions
To convert a mixed number to an improper fraction:
- Multiply the whole number by the denominator:
- For 2 3/4: 2 * 4 = 8
- Add the numerator to the result:
- 8 + 3 = 11
- Place the result over the original denominator:
- So, 2 3/4 = 11/4
4.3.2 Comparing Improper Fractions
Once the mixed numbers are converted to improper fractions, you can compare them using any of the methods discussed earlier (common denominator, cross-multiplication, or converting to decimals).
-
Example: Compare 2 3/4 and 3 1/5 by converting to improper fractions.
- 2 3/4 = (2 * 4 + 3) / 4 = 11/4
- 3 1/5 = (3 * 5 + 1) / 5 = 16/5
- Now compare 11/4 and 16/5 using cross-multiplication:
- 11 * 5 = 55
- 16 * 4 = 64
- Since 64 > 55, 16/5 is greater than 11/4.
- Therefore, 3 1/5 is greater than 2 3/4.
4.4 Examples Of Comparing Mixed Numbers
Let’s look at some examples to illustrate these methods:
-
Example 1: Compare 5 1/3 and 5 2/7.
- The whole number parts are the same (5), so we compare the fractions 1/3 and 2/7.
- Using cross-multiplication:
- 1 * 7 = 7
- 2 * 3 = 6
- Since 7 > 6, 1/3 > 2/7.
- Therefore, 5 1/3 > 5 2/7.
-
Example 2: Compare 2 2/5 and 3 1/4.
- The whole number part of 2 2/5 is 2, and the whole number part of 3 1/4 is 3.
- Since 3 > 2, 3 1/4 > 2 2/5.
-
Example 3: Compare 1 3/8 and 1 5/16.
- The whole number parts are the same (1), so we compare the fractions 3/8 and 5/16.
- Using a common denominator (16):
- 3/8 = 6/16
- Now compare 6/16 and 5/16.
- Since 6/16 > 5/16, 1 3/8 > 1 5/16.
4.5 Practice Problems
Test your understanding with these practice problems:
- Compare 2 1/4 and 2 3/5.
- Compare 3 2/7 and 4 1/3.
- Compare 1 5/8 and 1 9/16.
Answers: 1. 2 3/5 > 2 1/4, 2. 4 1/3 > 3 2/7, 3. 1 5/8 > 1 9/16
5. Comparing More Than Two Fractions
When you need to compare more than two fractions, the process involves extending the methods used for comparing two fractions. The most common approach is to find a common denominator for all the fractions.
5.1 Finding A Common Denominator For Multiple Fractions
To compare multiple fractions, you must first find a common denominator. The least common denominator (LCD) is the smallest multiple that all the denominators can divide into evenly.
5.1.1 How To Find The LCD For Multiple Fractions
-
List the multiples of each denominator: For example, if you’re comparing 1/3, 1/4, and 2/5:
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, …
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, …
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, …
-
Identify the smallest multiple that appears in all lists: In this case, the smallest common multiple is 60. Therefore, the LCD of 3, 4, and 5 is 60.
5.1.2 Converting Fractions To Have The LCD
Once you’ve found the LCD, convert each fraction so that its denominator matches the LCD. To do this, multiply both the numerator and the denominator of each fraction by the factor that makes the original denominator equal to the LCD.
-
For 1/3: To convert the denominator 3 to 60, multiply by 20. So, multiply both the numerator and denominator by 20:
- (1 20) / (3 20) = 20/60
-
For 1/4: To convert the denominator 4 to 60, multiply by 15. So, multiply both the numerator and denominator by 15:
- (1 15) / (4 15) = 15/60
-
For 2/5: To convert the denominator 5 to 60, multiply by 12. So, multiply both the numerator and denominator by 12:
- (2 12) / (5 12) = 24/60
5.2 Comparing Numerators
After converting all fractions to have the same denominator, you can easily compare the numerators. The fraction with the largest numerator is the largest fraction, and the fraction with the smallest numerator is the smallest fraction.
-
Example: Compare 20/60, 15/60, and 24/60.
- The numerators are 20, 15, and 24.
- Since 24 > 20 > 15, the order from largest to smallest is 24/60, 20/60, and 15/60.
- Therefore, the order of the original fractions from largest to smallest is 2/5, 1/3, and 1/4.
5.3 Examples Of Comparing Multiple Fractions
Let’s look at some examples to illustrate this process:
-
Example 1: Compare 1/2, 2/5, and 3/10.
- The LCD of 2, 5, and 10 is 10.
- Convert 1/2 to 5/10 (multiply both numerator and denominator by 5).
- Convert 2/5 to 4/10 (multiply both numerator and denominator by 2).
- The fractions are now 5/10, 4/10, and 3/10.
- Comparing the numerators: 5 > 4 > 3.
- Therefore, the order from largest to smallest is 1/2, 2/5, and 3/10.
-
Example 2: Compare 2/3, 3/4, and 5/6.
- The LCD of 3, 4, and 6 is 12.
- Convert 2/3 to 8/12 (multiply both numerator and denominator by 4).
- Convert 3/4 to 9/12 (multiply both numerator and denominator by 3).
- Convert 5/6 to 10/12 (multiply both numerator and denominator by 2).
- The fractions are now 8/12, 9/12, and 10/12.
- Comparing the numerators: 10 > 9 > 8.
- Therefore, the order from largest to smallest is 5/6, 3/4, and 2/3.
-
Example 3: Compare 1/4, 2/7, and 3/14.
- The LCD of 4, 7, and 14 is 28.
- Convert 1/4 to 7/28 (multiply both numerator and denominator by 7).
- Convert 2/7 to 8/28 (multiply both numerator and denominator by 4).
- Convert 3/14 to 6/28 (multiply both numerator and denominator by 2).
- The fractions are now 7/28, 8/28, and 6/28.
- Comparing the numerators: 8 > 7 > 6.
- Therefore, the order from largest to smallest is 2/7, 1/4, and 3/14.
5.4 Practice Problems
Test your skills with these practice problems:
- Compare 1/3, 2/5, and 3/8.
- Compare 2/7, 3/10, and 4/15.
- Compare 1/6, 3/10, and 2/5.
Answers: 1. 2/5 > 3/8 > 1/3, 2. 3/10 > 4/15 > 2/7, 3. 2/5 > 3/10 > 1/6
6. Tips And Tricks For Easier Comparison
Comparing fractions can be simplified with a few handy tips and tricks. These strategies can help you quickly assess the relative sizes of fractions without going through lengthy calculations.
6.1 Benchmarking With 1/2
One useful technique is to benchmark fractions against 1/2. This involves determining whether each fraction is greater than, less than, or equal to 1/2.
6.1.1 How To Use Benchmarking
- Compare each fraction to 1/2:
- A fraction is greater than 1/2 if its numerator is more than half of its denominator.
- A fraction is less than 1/2 if its numerator is less than half of its denominator.
- A fraction is equal to 1/2 if its numerator is exactly half of its denominator.
- Use the comparison to determine the relative sizes of the fractions:
- If one fraction is greater than 1/2 and another is less than 1/2, the one greater than 1/2 is larger.
- If both fractions are greater than 1/2 or both are less than 1/2, you’ll need to use another method (like finding a common denominator) to compare them.
6.1.2 Examples Of Benchmarking
-
Example 1: Compare 3/5 and 2/7.
- 3/5: Half of 5 is 2.5. Since 3 > 2.5, 3/5 is greater than 1/2.
- 2/7: Half of 7 is 3.5. Since 2 < 3.5, 2/7 is less than 1/2.
- Therefore, 3/5 > 2/7.
-
Example 2: Compare 4/6 and 5/9.
- 4/6: Half of 6 is 3. Since 4 > 3, 4/6 is greater than 1/2.
- 5/9: Half of 9 is 4.5. Since 5 > 4.5, 5/9 is greater than 1/2.
- Since both are greater than 1/2, use another method (like finding a common denominator) to compare them.
- 4/6 = 12/18
- 5/9 = 10/18
- Thus, 4/6 > 5/9.
6.2 Comparing To 0 And 1
Another useful tip is to compare fractions to 0 and 1. This helps quickly identify whether a fraction is very small or very large relative to the whole.
6.2.1 How To Use This Comparison
- Assess each fraction in relation to 0 and 1:
- A fraction is close to 0 if its numerator is much smaller than its denominator.
- A fraction is close to 1 if its numerator is very close to its denominator.
- Use these assessments to compare the fractions:
- If one fraction is close to 1 and another is close to 0, the one close to 1 is larger.
- If both fractions are close to 0 or both are close to 1, you’ll need to use another method to compare them more precisely.
6.2.2 Examples Of Comparing To 0 And 1
-
Example 1: Compare 1/10 and 9/10.
- 1/10: The numerator (1) is much smaller than the denominator (10), so it’s close to 0.
- 9/10: The numerator (9) is very close to the denominator (10), so it’s close to 1.
- Therefore, 9/10 > 1/10.
-
Example 2: Compare 2/11 and 3/13.
- 2/11: The numerator (2) is small compared to the denominator (11), so it’s closer to 0.
- 3/13: The numerator (3) is also small compared to the denominator (13), so it’s also closer to 0.
- Since both are close to 0, use another method to compare them.
- 2/11 = 26/143
- 3/13 = 33/143
- Thus, 3/13 > 2/11.
6.3 Estimating And Approximating
Estimating and approximating fractions can help you quickly determine their relative sizes, especially when exact comparisons are not necessary.
6.3.1 How To Estimate Fractions
- Round the fractions to the nearest simple fraction: This might involve rounding the numerator or denominator to make the fraction easier to work with.
- Compare the rounded fractions: Use your knowledge of simple fractions to quickly estimate their sizes.
6.3.2 Examples Of Estimating Fractions
-
Example 1: Compare 7/15 and 9/20.
- 7/15 is approximately 7/14, which simplifies to 1/2.
- 9/20 is slightly less than 10/20, which simplifies to 1/2.
- Since both are approximately 1/2, use another method to compare them more accurately.
- 7/15 = 28/60
- 9/20 = 27/60
- Thus, 7/15 > 9/20.
-
Example 2: Compare 16/33 and 19/40.
- 16/33 is approximately 16/32, which simplifies to 1/2.
- 19/40 is slightly less than 20/40, which simplifies to 1/2.
- Since both are approximately 1/2, use another method to compare them more accurately.
- 16/33 = 640/1320
- 19/40 = 627/1320
- Thus, 16/33 > 19/40.
6.4 Practice Problems
Use these tips to quickly compare the following fractions:
- Compare 4/9 and 6/13 using benchmarking with 1/2.
- Compare 2/15 and 8/9 using comparison to 0 and 1.
- Compare 11/23 and 13/27 using estimation.
Answers: 1. 6/13 > 4/9, 2. 8/9 > 2/15, 3. 11/23 > 13/27
7. Real-World Applications Of Comparing Fractions
Comparing fractions isn’t just a theoretical exercise; it has many practical applications in everyday life. Understanding how to compare fractions can help you make better decisions in various situations.
7.1 Cooking And Baking
In cooking and baking, recipes often require you to adjust ingredient quantities. Comparing fractions is essential for scaling recipes up or down accurately.
-
Example: A recipe calls for 2/3 cup of flour, but you only want to make half the recipe. You need to determine what half of 2/3 is.
- Half of 2/3 is (1/2) * (2/3) = 1/3 cup.
- Therefore, you would use 1/3 cup of flour.
7.2 Measuring And Construction
In measuring and construction, comparing fractions helps ensure precision and accuracy in dimensions and proportions.
-
Example: You need to cut a piece of wood that is 3/8 inch thick, but your ruler only shows measurements in 1/16 inch increments.
- Convert 3/8 to sixteenths: (3/8) * (2/2) = 6/16 inch.
- You can now accurately measure and cut the wood to the correct thickness.
7.3 Finances And Budgeting
Understanding fractions is crucial for managing personal finances, comparing prices, and budgeting effectively.
-
Example: You’re comparing two investment options: one offers a return of 1/4 of your investment, and the other offers a return of 2/10.
- Compare 1/4 and 2/10:
- 1/4 = 5/20
- 2/10 = 4/20
- Since 5/20 > 4/20, the first investment option (1/4) offers a better return.
- Compare 1/4 and 2/10:
7.4 Time Management
Comparing fractions can help you manage your time more effectively by estimating how long different tasks will take and prioritizing accordingly.
-
Example: You have three tasks to complete: one will take 1/3 of your day, another will take 1/4 of your day, and the third will take 1/6 of your day.
- Compare 1/3, 1/4, and 1/6:
- LCD = 12
- 1/3 = 4/12
- 1/4 = 3/12
- 1/6 = 2/12
- The tasks in order of time consumption are: 1/3 > 1/4 > 1/6.
- You can prioritize the task that takes 1/3 of your day first.
- Compare 1/3, 1/4, and 1/6:
7.5 Practice Problems
Consider these real-world scenarios and use your fraction comparison skills to solve them:
- A recipe calls for 3/4 teaspoon of salt. If you want to double the recipe, how much salt do you need?
- You need to divide a 5-meter ribbon into two pieces: one that is 2/5 of the total length and the other that is 3/5. How long is each piece?
- You are offered a discount of 1/3 off the original price of an item. Would you prefer this discount or a discount of 3/10 off the original price?
Answers: 1. 1 1/2 teaspoons, 2. 2 meters and 3 meters, 3. 1/3 off is better
8. Common Mistakes To Avoid When Comparing Fractions
When comparing fractions, it’s easy to make mistakes if you’re not careful. Being aware of these common pitfalls can help you avoid errors and ensure accurate comparisons.
8.1 Assuming Larger Denominator Means Larger Fraction
One of the most common mistakes is assuming that a fraction with a larger denominator is always smaller. This is only true when the numerators are the same.
- Mistake: Thinking that 1/8 is smaller than 1/4 because 8 is larger than 4.
- Correction: Remember that when numerators are the same, the fraction with the smaller denominator is actually larger because it represents a whole divided into fewer parts. In this case, 1/4 > 1/8.
8.2 Forgetting To Find A Common Denominator
When comparing fractions with different denominators, it’s essential to find a common denominator before comparing the numerators.