Do you compare mole in solute vs solvent? Understanding the mole fraction in solute versus solvent is crucial for comprehending solution behavior, especially in relation to Raoult’s Law. COMPARE.EDU.VN provides comprehensive comparisons and analyses to simplify complex scientific concepts. This guide breaks down the essentials, ensuring you grasp the nuances of solute-solvent interactions, ideal solutions, and vapor pressure calculations, all while optimizing your understanding of colligative properties and solution chemistry.
1. What is the Significance of Comparing Moles in Solute vs. Solvent?
Comparing moles of solute and solvent is fundamental in understanding the properties of solutions. The relative amounts of each component influence the solution’s colligative properties, such as vapor pressure, boiling point, and freezing point. This comparison helps predict and explain how the solution behaves under different conditions.
1.1 Mole Fraction Explained
Mole fraction is a way to express the concentration of a component in a mixture or solution. It’s defined as the number of moles of a particular component divided by the total number of moles of all components in the mixture.
-
Formula:
[
text{Mole fraction of component A} = frac{text{Moles of A}}{text{Total moles of all components}}
] -
Importance: Mole fraction is dimensionless, making it easy to compare concentrations across different solutions and conditions. It’s especially useful in Raoult’s Law calculations.
1.2 Why Mole Fraction Matters in Solutions
Mole fraction plays a critical role because it directly impacts the physical properties of solutions. For instance, in Raoult’s Law, the vapor pressure of a solution is proportional to the mole fraction of the solvent. This relationship helps predict how a solution will behave under different temperatures and pressures.
1.3 Real-world Applications
Understanding mole fractions is essential in various fields:
- Chemistry: Predicting reaction rates and equilibrium conditions.
- Pharmaceuticals: Calculating drug concentrations in formulations.
- Environmental Science: Assessing pollutant levels in water or air samples.
- Chemical Engineering: Designing and optimizing chemical processes.
2. Understanding Solute and Solvent Roles
Solute and solvent play distinct roles in a solution. The solute is the substance being dissolved, while the solvent is the substance doing the dissolving. The interaction between these two determines the solution’s properties.
2.1 Defining Solute and Solvent
- Solute: The component present in a smaller amount that dissolves in the solvent.
- Solvent: The component present in a larger amount that dissolves the solute.
For example, in a salt water solution, salt is the solute and water is the solvent.
2.2 Factors Affecting Solubility
Solubility, the ability of a solute to dissolve in a solvent, depends on several factors:
- Temperature: Solubility of solids usually increases with temperature, while gases often decrease.
- Pressure: Primarily affects the solubility of gases; higher pressure increases solubility.
- Polarity: “Like dissolves like”—polar solutes dissolve in polar solvents, and nonpolar solutes dissolve in nonpolar solvents.
- Intermolecular Forces: Stronger forces between solute and solvent molecules enhance solubility.
2.3 Types of Solutions
Solutions can be classified based on the state of the solute and solvent:
- Gaseous Solutions: Gas dissolved in gas (e.g., air).
- Liquid Solutions: Solid, liquid, or gas dissolved in a liquid (e.g., salt water, alcohol in water, carbonated water).
- Solid Solutions: Solid dissolved in solid (e.g., alloys like brass).
3. Raoult’s Law: The Key Relationship
Raoult’s Law describes the relationship between the vapor pressure of a solution and the mole fraction of the solvent. This law is fundamental in understanding the colligative properties of solutions.
3.1 What is Raoult’s Law?
Raoult’s Law states that the vapor pressure of a solvent above a solution is equal to the vapor pressure of the pure solvent at the same temperature, scaled by the mole fraction of the solvent present.
-
Formula:
[
P{text{solution}} = chi{text{solvent}} P^o_{text{solvent}}
]Where:
- (P_{text{solution}}) is the vapor pressure of the solution.
- (chi_{text{solvent}}) is the mole fraction of the solvent.
- (P^o_{text{solvent}}) is the vapor pressure of the pure solvent.
3.2 Assumptions and Limitations
Raoult’s Law works best under ideal conditions, which include:
- Ideal Solutions: Solutions where intermolecular interactions between solute and solvent are similar to those between the pure components.
- Dilute Solutions: Solutions with a low concentration of solute.
However, Raoult’s Law has limitations:
- Non-ideal Solutions: Significant deviations occur when solute-solvent interactions differ greatly from pure component interactions.
- Concentrated Solutions: The law is less accurate at higher solute concentrations.
- Volatile Solutes: Raoult’s Law in its simplest form applies mainly when the solute is non-volatile.
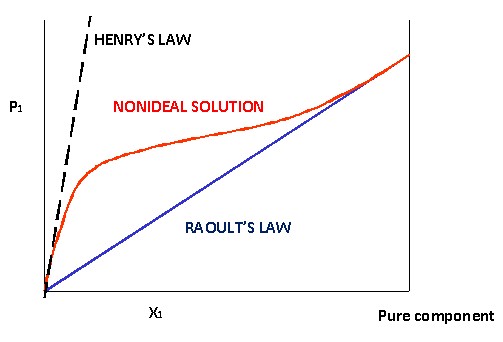
3.3 Ideal vs. Non-ideal Solutions
- Ideal Solutions: Exhibit thermodynamic mixing characteristics identical to those of ideal gas mixtures. Intermolecular interactions are equal to those of the pure components.
- Non-ideal Solutions: Do not follow Raoult’s Law accurately due to significant differences in intermolecular forces between solute and solvent.
3.4 Positive and Negative Deviations
Non-ideal solutions can show positive or negative deviations from Raoult’s Law:
- Positive Deviation: Occurs when solute-solvent interactions are weaker than those in the pure components, leading to a higher vapor pressure than predicted.
- Negative Deviation: Occurs when solute-solvent interactions are stronger, resulting in a lower vapor pressure than predicted.
3.5 Factors Influencing Deviations
Several factors influence deviations from Raoult’s Law:
- Chemical Nature: Differences in the chemical properties of solute and solvent.
- Temperature: Affects the strength of intermolecular forces.
- Concentration: Higher concentrations increase the likelihood of non-ideal behavior.
4. Calculating Vapor Pressure Using Raoult’s Law
Calculating vapor pressure using Raoult’s Law involves determining the mole fraction of the solvent and using the vapor pressure of the pure solvent. The approach varies based on whether the solute is volatile or non-volatile.
4.1 Non-Volatile Solutes
When the solute is non-volatile, it does not contribute to the vapor pressure. The calculation is straightforward:
- Determine Moles: Calculate the number of moles of both solute and solvent.
- Calculate Mole Fraction: Find the mole fraction of the solvent.
- Apply Raoult’s Law: Use the formula (P{text{solution}} = chi{text{solvent}} P^o_{text{solvent}}) to find the vapor pressure of the solution.
-
Example:
If 1.5 moles of solute are added to 110.9 moles of water, and the vapor pressure of pure water is 23.8 mm Hg:
[
chi_{text{water}} = frac{110.9}{110.9 + 1.5} = 0.9867
][
P_{text{solution}} = 0.9867 times 23.8 = 23.48 , text{mm Hg}
]
4.2 Volatile Solutes
When the solute is volatile, it contributes to the vapor pressure, and you must consider the partial pressures of both solute and solvent.
-
Determine Moles: Calculate the number of moles of both solute and solvent.
-
Calculate Mole Fractions: Find the mole fractions of both solute and solvent.
-
Calculate Partial Pressures: Use Raoult’s Law to find the partial pressure of each component:
[
P{text{solute}} = chi{text{solute}} P^o_{text{solute}}
][
P{text{solvent}} = chi{text{solvent}} P^o_{text{solvent}}
] -
Calculate Total Vapor Pressure: Add the partial pressures to find the total vapor pressure of the solution:
[
P{text{total}} = P{text{solute}} + P_{text{solvent}}
]
-
Example:
For a solution with a mole fraction of benzene of 0.6 and toluene of 0.4, where (P^o{text{benzene}} = 95.1) mm Hg and (P^o{text{toluene}} = 28.4) mm Hg:
[
P_{text{benzene}} = 0.6 times 95.1 = 57.06 , text{mm Hg}
][
P_{text{toluene}} = 0.4 times 28.4 = 11.36 , text{mm Hg}
][
P_{text{total}} = 57.06 + 11.36 = 68.42 , text{mm Hg}
]
4.3 Step-by-step Calculation
Here’s a step-by-step approach for calculating vapor pressure:
- Identify Solute and Solvent: Determine which substance is the solute and which is the solvent.
- Calculate Moles: Convert the mass of each component to moles using their respective molar masses.
- Determine Mole Fractions: Calculate the mole fractions of both solute and solvent.
- Find Vapor Pressures: Obtain the vapor pressures of the pure solute and solvent at the given temperature.
- Apply Raoult’s Law: Use the appropriate formulas based on whether the solute is volatile or non-volatile.
- Calculate Total Vapor Pressure: Sum the partial pressures if both components are volatile.
5. Factors Affecting Vapor Pressure
Several factors can influence the vapor pressure of a solution. Understanding these factors is essential for accurate predictions and applications.
5.1 Temperature
Temperature significantly affects vapor pressure. As temperature increases, the kinetic energy of the molecules also increases, allowing more molecules to escape into the gas phase.
- Impact: Higher temperature leads to higher vapor pressure.
5.2 Intermolecular Forces
The strength of intermolecular forces between solute and solvent molecules affects vapor pressure. Stronger attractive forces reduce the tendency of molecules to escape into the gas phase.
- Impact: Stronger forces lead to lower vapor pressure.
5.3 Solute Concentration
The concentration of the solute in the solution also plays a role. As the solute concentration increases, the mole fraction of the solvent decreases, leading to a lower vapor pressure (as per Raoult’s Law).
- Impact: Higher solute concentration generally leads to lower vapor pressure.
5.4 Volatility of Components
The volatility of the solute and solvent also affects the vapor pressure. Volatile substances have higher vapor pressures because they readily evaporate.
- Impact: More volatile components contribute more to the overall vapor pressure.
6. Practical Examples and Exercises
Applying the concepts of mole fraction and Raoult’s Law through practical examples and exercises helps solidify understanding.
6.1 Example 1: Non-Electrolyte Solution
Calculate the vapor pressure of a solution made by dissolving 50.0 g of glucose ((C6H{12}O_6)) in 500 g of water at 37°C. The vapor pressure of pure water at this temperature is 47.1 torr.
-
Moles of Water:
[
n_{text{water}} = frac{500 , text{g}}{18 , text{g/mol}} = 27.7 , text{mol}
] -
Moles of Glucose:
[
n_{text{glucose}} = frac{50 , text{g}}{180.2 , text{g/mol}} = 0.277 , text{mol}
] -
Mole Fraction of Water:
[
chi_{text{water}} = frac{27.7}{27.7 + 0.277} = 0.99
] -
Vapor Pressure of Solution:
[
P_{text{solution}} = 0.99 times 47.1 = 46.63 , text{torr}
]
6.2 Example 2: Electrolyte Solution
Calculate the vapor pressure of a solution made by dissolving 50.0 g of (CaCl_2) in 500 g of water at 37°C. The vapor pressure of pure water at this temperature is 47.1 torr.
-
Moles of Water:
[
n_{text{water}} = frac{500 , text{g}}{18 , text{g/mol}} = 27.7 , text{mol}
] -
Moles of (CaCl_2):
[
n_{text{CaCl}_2} = frac{50 , text{g}}{111 , text{g/mol}} = 0.45 , text{mol}
]Since (CaCl_2) dissociates into three ions ((Ca^{2+}) and 2 (Cl^{-})), the total moles of solute particles are:
[
n_{text{solutes}} = 0.45 + (2 times 0.45) = 1.35 , text{mol}
] -
Mole Fraction of Water:
[
chi_{text{water}} = frac{27.7}{27.7 + 1.35} = 0.953
] -
Vapor Pressure of Solution:
[
P_{text{solution}} = 0.953 times 47.1 = 44.88 , text{torr}
]
6.3 Practice Exercises
- What is the vapor pressure of a solution at 25°C containing 78.0 grams of glucose (MM = 180.16 g/mol) in 500 grams of water? The vapor pressure of pure water at this temperature is 23.8 mm Hg.
- 25 grams of cyclohexane ((P^o = 80.5) torr, MM = 84.16 g/mol) and 30 grams of ethanol ((P^o = 52.3) torr, MM = 92.14 g/mol) are both volatile components present in a solution. What is the partial pressure of ethanol?
- What is the vapor pressure of pure butane at 20°C if its partial pressure is 698 mm Hg in a butane-acetone mixture where the mole fraction of acetone is x = 0.577?
7. Raoult’s Law and Colligative Properties
Raoult’s Law is closely linked to colligative properties, which are properties of solutions that depend on the number of solute particles rather than their chemical identity.
7.1 Colligative Properties Defined
Colligative properties include:
- Vapor Pressure Lowering: The vapor pressure of a solution is lower than that of the pure solvent.
- Boiling Point Elevation: The boiling point of a solution is higher than that of the pure solvent.
- Freezing Point Depression: The freezing point of a solution is lower than that of the pure solvent.
- Osmotic Pressure: The pressure required to stop the flow of solvent across a semipermeable membrane.
7.2 How Raoult’s Law Relates
Raoult’s Law directly explains vapor pressure lowering. Because the vapor pressure of a solution is proportional to the mole fraction of the solvent, adding a solute reduces the solvent’s mole fraction, thereby lowering the vapor pressure.
- Boiling Point Elevation: The boiling point increases because a higher temperature is needed for the solution’s vapor pressure to equal the atmospheric pressure.
- Freezing Point Depression: The freezing point decreases because the presence of solute particles disrupts the formation of the solvent’s crystal lattice.
7.3 Practical Applications of Colligative Properties
Colligative properties have numerous practical applications:
- Antifreeze in Cars: Ethylene glycol is added to water to lower its freezing point and raise its boiling point, preventing the engine from freezing or overheating.
- Salting Roads: Salt is used to melt ice on roads in winter, lowering the freezing point of water.
- Osmosis in Biology: Osmotic pressure is crucial for maintaining cell turgor and function in living organisms.
- Reverse Osmosis: Used in water purification to remove solutes from water, creating potable water from seawater or contaminated sources.
8. Common Mistakes to Avoid
When working with Raoult’s Law and mole fractions, it’s important to avoid common mistakes that can lead to incorrect calculations.
8.1 Forgetting Electrolyte Dissociation
Electrolytes dissociate into ions in solution. Failing to account for this dissociation can lead to errors in calculating the total number of moles of solute particles.
- Example: (NaCl) dissociates into (Na^+) and (Cl^-), so 1 mole of (NaCl) produces 2 moles of particles.
8.2 Ignoring Non-Ideal Behavior
Raoult’s Law assumes ideal behavior, which is not always the case. Ignoring non-ideal behavior can lead to significant deviations in calculated vapor pressures.
- Solution: Consider using activity coefficients or more advanced models for non-ideal solutions.
8.3 Incorrectly Calculating Mole Fractions
Errors in calculating mole fractions, such as using incorrect molar masses or not accounting for all components, can lead to inaccurate results.
- Solution: Double-check molar masses and ensure all components are included in the calculation.
8.4 Mixing Up Solute and Solvent
Confusing solute and solvent can lead to incorrect calculations. Always clearly identify which substance is the solute and which is the solvent.
- Solution: Clearly label each component and its corresponding properties.
8.5 Neglecting Temperature Dependence
Vapor pressures are temperature-dependent. Using vapor pressure values at the wrong temperature can lead to inaccurate results.
- Solution: Ensure you are using the correct vapor pressure values for the given temperature.
9. Advanced Topics in Solution Chemistry
Beyond Raoult’s Law, several advanced topics in solution chemistry provide a deeper understanding of solution behavior.
9.1 Activity and Activity Coefficients
In non-ideal solutions, activity and activity coefficients are used to correct for deviations from Raoult’s Law. Activity represents the “effective concentration” of a component, while the activity coefficient is a measure of how much a substance deviates from ideal behavior.
-
Formula:
[
a_i = gamma_i chi_i
]Where:
- (a_i) is the activity of component i.
- (gamma_i) is the activity coefficient of component i.
- (chi_i) is the mole fraction of component i.
9.2 Fugacity and Fugacity Coefficients
Fugacity is a measure of the “escaping tendency” of a substance from a particular phase, similar to vapor pressure but applicable to real gases and liquids. The fugacity coefficient corrects for non-ideal behavior in gases.
- Application: Used in chemical engineering for designing and analyzing processes involving real gases.
9.3 Excess Properties
Excess properties describe the difference between the actual properties of a mixture and the properties it would have if it were an ideal solution. These properties include excess volume, excess enthalpy, and excess entropy.
- Importance: Provide insights into the nature of intermolecular interactions in non-ideal solutions.
9.4 Models for Non-Ideal Solutions
Various models are used to describe non-ideal solutions, including:
- Regular Solution Theory: Assumes that the excess entropy of mixing is zero.
- UNIFAC (Universal Functional Activity Coefficient): A group contribution method that estimates activity coefficients based on the functional groups present in the molecules.
- NRTL (Non-Random Two-Liquid): An activity coefficient model that accounts for local composition effects in solutions.
10. How COMPARE.EDU.VN Can Help
COMPARE.EDU.VN offers comprehensive resources to help you understand and compare complex scientific concepts, including Raoult’s Law and solution chemistry.
10.1 Detailed Comparisons and Analyses
COMPARE.EDU.VN provides detailed comparisons of various scientific principles and applications, making it easier to grasp complex concepts.
- Benefits: Clear, concise explanations and examples to enhance understanding.
10.2 Real-World Examples and Case Studies
Explore real-world examples and case studies that illustrate the practical applications of Raoult’s Law and colligative properties.
- Benefits: Understand how these concepts are used in various fields, such as pharmaceuticals, environmental science, and chemical engineering.
10.3 Expert Insights and Explanations
Gain access to expert insights and explanations that simplify complex scientific topics.
- Benefits: Clarify doubts and deepen your understanding with reliable and accurate information.
10.4 Interactive Tools and Resources
Utilize interactive tools and resources, such as calculators and simulations, to reinforce your understanding of mole fractions and vapor pressure calculations.
- Benefits: Hands-on learning experiences that make complex concepts more accessible.
FAQ: Mole Fraction and Raoult’s Law
1. What is the difference between mole fraction and molarity?
Mole fraction is the ratio of the number of moles of a component to the total number of moles in the solution, while molarity is the number of moles of solute per liter of solution.
2. Can Raoult’s Law be applied to all solutions?
No, Raoult’s Law is most accurate for ideal and dilute solutions. Non-ideal solutions may exhibit significant deviations.
3. How does temperature affect vapor pressure?
Increasing temperature generally increases vapor pressure because more molecules have enough energy to escape into the gas phase.
4. What are colligative properties?
Colligative properties are properties of solutions that depend on the number of solute particles, not their chemical identity. Examples include vapor pressure lowering, boiling point elevation, and freezing point depression.
5. Why is it important to consider electrolyte dissociation when using Raoult’s Law?
Electrolytes dissociate into ions in solution, increasing the number of solute particles. This must be accounted for when calculating mole fractions and applying Raoult’s Law.
6. What is a non-volatile solute?
A non-volatile solute is a substance that does not readily evaporate into the gas phase at a given temperature.
7. What is the significance of activity coefficients?
Activity coefficients correct for non-ideal behavior in solutions, providing a more accurate representation of the “effective concentration” of a component.
8. How does COMPARE.EDU.VN simplify complex scientific concepts?
COMPARE.EDU.VN provides detailed comparisons, real-world examples, expert insights, and interactive tools to make complex scientific concepts more accessible and understandable.
9. What are some practical applications of colligative properties?
Practical applications include antifreeze in cars, salting roads to melt ice, and reverse osmosis for water purification.
10. Where can I find more detailed explanations and examples of Raoult’s Law?
You can find more detailed explanations and examples on COMPARE.EDU.VN, which offers comprehensive resources for understanding scientific principles.
Conclusion
Understanding the comparison of moles in solute versus solvent, especially in the context of Raoult’s Law, is essential for grasping the behavior of solutions. COMPARE.EDU.VN provides the tools and resources you need to master these concepts, from detailed explanations to practical examples. By exploring the factors that affect vapor pressure and learning to avoid common mistakes, you can confidently apply Raoult’s Law in various scientific and practical contexts.
Ready to dive deeper and make informed decisions? Visit COMPARE.EDU.VN today to explore detailed comparisons and analyses that simplify complex topics. Make your learning journey easier and more effective with COMPARE.EDU.VN.
Contact Information:
Address: 333 Comparison Plaza, Choice City, CA 90210, United States
Whatsapp: +1 (626) 555-9090
Website: compare.edu.vn