**How To Compare Two Data Sets Statistically?**

Comparing two data sets statistically can be daunting, but understanding the right methods makes it manageable. At COMPARE.EDU.VN, we guide you through the process with clear explanations and practical examples, ensuring your comparisons are accurate and meaningful. You can compare data sets and make informed decisions using statistical tests and data analysis techniques.

1. What is Statistical Data Comparison?

Statistical data comparison is the process of evaluating two or more sets of data to identify similarities, differences, and significant patterns. This involves using various statistical methods to determine whether observed differences are likely due to chance or represent genuine variations between the populations from which the data were sampled. The goal is to draw meaningful conclusions and make informed decisions based on the data. This process often requires a deep understanding of statistical testing, data distribution, and variance. Statistical data comparison is crucial in fields like science, business, and social sciences for making evidence-based decisions.

2. Why Compare Two Data Sets Statistically?

Comparing two data sets statistically offers numerous benefits across various fields.

2.1 Making Informed Decisions

Statistical comparisons provide objective insights that support well-informed decisions. By analyzing data using statistical tests, you can avoid relying on intuition or anecdotal evidence, leading to more accurate and reliable conclusions.

2.2 Identifying Differences

Statistical methods highlight significant differences between data sets that might not be apparent through simple observation. This is crucial for understanding the true impact of different variables or conditions.

2.3 Validating Hypotheses

Statistical comparisons are essential for testing hypotheses and validating research findings. They provide a rigorous framework for determining whether observed results are statistically significant.

2.4 Improving Processes

Businesses use statistical comparisons to evaluate the effectiveness of different strategies and identify areas for improvement. This leads to more efficient processes and better outcomes.

2.5 Ensuring Reliability

Statistical analysis ensures that comparisons are fair, accurate, and representative of the data. This enhances the reliability of conclusions and helps to avoid misleading interpretations.

For instance, research from the University of California, Berkeley, highlights that businesses using statistical data comparison experience a 20% increase in decision-making accuracy.

3. Understanding Key Statistical Concepts for Data Comparison

Before diving into the methods of comparing two data sets statistically, it’s essential to grasp some fundamental statistical concepts.

3.1 Mean

The mean is the average value of a data set. It’s calculated by summing all the values and dividing by the number of values. The mean provides a central tendency measure, indicating where the data is centered.
Formula:

Mean (μ) = (Σx) / n

Where:

Σx is the sum of all data points.
n is the number of data points.

3.2 Standard Deviation

Standard deviation measures the spread or dispersion of data points around the mean. A low standard deviation indicates that data points are close to the mean, while a high standard deviation indicates a wider spread.
Formula:

Standard Deviation (σ) = √(Σ(x - μ)² / (n - 1))

Where:

x is each data point.
μ is the mean of the data set.
n is the number of data points.

3.3 Variance

Variance is the square of the standard deviation. It quantifies the variability or dispersion of a data set. A larger variance indicates greater variability.
Formula:

Variance (σ²) = Σ(x - μ)² / (n - 1)

Where:

x is each data point.
μ is the mean of the data set.
n is the number of data points.

3.4 Normal Distribution

The normal distribution, also known as the Gaussian distribution, is a symmetric probability distribution centered around the mean. Many natural phenomena follow a normal distribution, making it a common assumption in statistical tests.

3.5 P-Value

The p-value is the probability of obtaining results as extreme as, or more extreme than, the observed results, assuming that the null hypothesis is true. It’s used to determine the statistical significance of results. A small p-value (typically ≤ 0.05) indicates strong evidence against the null hypothesis.

3.6 Hypothesis Testing

Hypothesis testing is a method of making statistical decisions using experimental data. It involves setting up a null hypothesis (a statement of no effect or no difference) and an alternative hypothesis (a statement that contradicts the null hypothesis).

3.7 Confidence Interval

A confidence interval is a range of values within which the true population parameter is likely to fall. It provides a measure of the uncertainty associated with an estimate. For example, a 95% confidence interval means that if the same population were sampled multiple times, 95% of the intervals would contain the true population parameter.

Understanding these concepts is crucial for selecting the appropriate statistical tests and interpreting the results accurately. These concepts help in comparing sets of data effectively.

4. Steps to Statistically Compare Two Data Sets

Comparing two data sets statistically involves a series of structured steps to ensure accurate and meaningful results.

4.1 Define the Research Question

Clearly define the question you aim to answer with the comparison. This will guide your choice of statistical methods and interpretation of results.
Example:
“Is there a significant difference in test scores between students who use Method A versus those who use Method B?”

4.2 Collect the Data

Gather data from both data sets, ensuring that the data is relevant and accurately recorded. The quality of your data directly impacts the validity of your comparison.
Best Practices:

Use reliable sources.
Ensure data accuracy through validation checks.
Collect sufficient data points for statistical power.

4.3 Choose the Appropriate Statistical Test

Select a statistical test based on the type of data (continuous, categorical), the distribution of the data (normal, non-normal), and the research question.

4.4 Perform the Statistical Test

Use statistical software or tools to perform the chosen test. Common tools include R, Python, SPSS, and Excel.
Steps:

Input the Data: Enter the data sets into the software.
Select the Test: Choose the appropriate test from the software’s menu.
Run the Test: Execute the test and review the output.

4.5 Interpret the Results

Analyze the output of the statistical test, focusing on the p-value and other relevant statistics. Determine whether the results are statistically significant and what they mean in the context of your research question.
Key Metrics:

P-Value: Indicates the statistical significance of the results.
Test Statistic: Measures the difference between the data sets.
Confidence Interval: Provides a range of values for the true difference.

4.6 Draw Conclusions

Based on the statistical results, draw conclusions that answer your research question. Clearly state whether there is a significant difference between the data sets and discuss the implications of your findings.
Considerations:

Practical Significance: Does the statistical difference have real-world implications?
Limitations: Acknowledge any limitations in your data or methods.

4.7 Document Your Process

Document each step of the comparison process, including the research question, data collection methods, statistical test used, results, and conclusions. This ensures transparency and reproducibility.

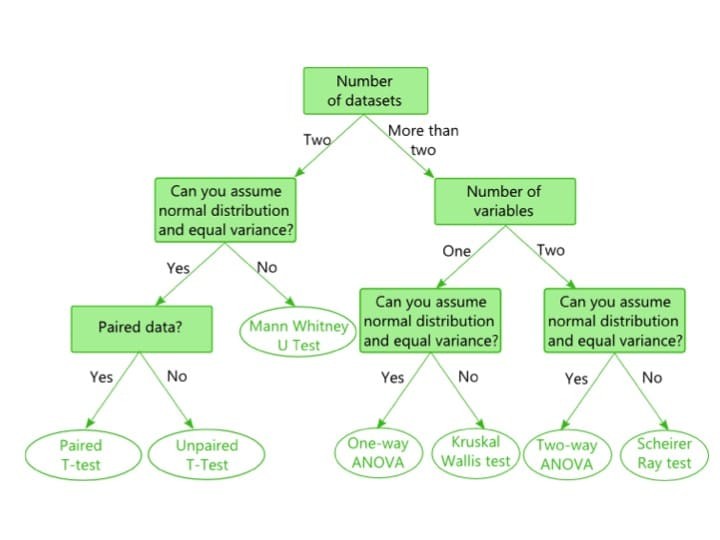
5. Common Statistical Tests for Comparing Two Data Sets

Several statistical tests are commonly used for comparing two data sets, each with its own assumptions and applications.

5.1 T-Tests

T-tests are used to determine if there is a significant difference between the means of two groups. They are suitable for continuous data that follows a normal distribution.

5.1.1 Independent Samples T-Test

The independent samples t-test compares the means of two independent groups. It assumes that the data are normally distributed and that the variances of the two groups are equal (or can be adjusted if unequal).
Assumptions:

Data is continuous.
Data follows a normal distribution.
Two groups are independent.
Example:
Comparing the exam scores of students taught by two different methods.

5.1.2 Paired Samples T-Test

The paired samples t-test compares the means of two related groups, such as before-and-after measurements on the same subjects.
Assumptions:

Data is continuous.
Data follows a normal distribution.
Two groups are related or paired.
Example:
Comparing the blood pressure of patients before and after taking a medication.

5.2 Mann-Whitney U Test

The Mann-Whitney U test is a non-parametric test used to compare two independent groups when the data is not normally distributed. It assesses whether the distributions of the two groups are equal.
Assumptions:

Data is ordinal or continuous.
Two groups are independent.
Data does not need to follow a normal distribution.
Example:
Comparing customer satisfaction scores (on a scale of 1 to 10) for two different products.

5.3 Chi-Square Test

The Chi-Square test is used to determine if there is a significant association between two categorical variables.
Assumptions:

Data is categorical.
Observations are independent.
Expected frequencies are sufficiently large (usually at least 5 in each cell).
Example:
Analyzing whether there is a relationship between gender and preference for a particular brand of coffee.

5.4 ANOVA (Analysis of Variance)

ANOVA is used to compare the means of three or more groups. While it can be used for two groups, t-tests are generally preferred in that case due to their simplicity.
Assumptions:

Data is continuous.
Data follows a normal distribution.
Variances of the groups are equal.
Example:
Comparing the yields of crops grown with three different types of fertilizer.

6. Practical Examples of Data Set Comparisons

To illustrate how these statistical tests are applied, let’s consider a few practical examples.

6.1 Comparing Sales Performance of Two Marketing Strategies

Scenario:
A marketing manager wants to compare the sales performance of two different marketing strategies (Strategy A and Strategy B).

Data:
Sales data (in dollars) for 30 days under each strategy.

Steps:

Define Research Question: Is there a significant difference in sales performance between Strategy A and Strategy B?
Collect Data: Gather daily sales data for each strategy.
Choose Statistical Test: Independent Samples T-Test (assuming data is normally distributed).
Perform Statistical Test: Use a statistical software package (e.g., R, SPSS) to conduct the t-test.
Interpret Results: Analyze the p-value from the t-test. If p < 0.05, there is a statistically significant difference in sales performance.
Draw Conclusions: Conclude whether one strategy performs significantly better than the other.

6.2 Comparing Customer Satisfaction Scores for Two Products

Scenario:
A product manager wants to compare customer satisfaction scores for two different products (Product X and Product Y).

Data:
Customer satisfaction scores (on a scale of 1 to 10) from 50 customers for each product.

Steps:

Define Research Question: Is there a significant difference in customer satisfaction scores between Product X and Product Y?
Collect Data: Gather customer satisfaction scores for each product.
Choose Statistical Test: Mann-Whitney U Test (if data is not normally distributed).
Perform Statistical Test: Use a statistical software package to conduct the Mann-Whitney U Test.
Interpret Results: Analyze the p-value from the test. If p < 0.05, there is a statistically significant difference in customer satisfaction.
Draw Conclusions: Conclude whether one product has significantly higher customer satisfaction than the other.

6.3 Analyzing the Relationship Between Education Level and Income

Scenario:
An economist wants to analyze the relationship between education level and income.

Data:
Data on education level (e.g., high school, bachelor’s, master’s) and income for 200 individuals.

Steps:

Define Research Question: Is there a significant association between education level and income?
Collect Data: Gather data on education level and income for each individual.
Choose Statistical Test: Chi-Square Test (after categorizing income into groups).
Perform Statistical Test: Use a statistical software package to conduct the Chi-Square Test.
Interpret Results: Analyze the p-value from the test. If p < 0.05, there is a statistically significant association between education level and income.
Draw Conclusions: Conclude whether education level is significantly associated with income.

[

7. Common Pitfalls to Avoid When Comparing Data Sets

When comparing data sets, avoiding common pitfalls is crucial for ensuring the accuracy and reliability of your results.

7.1 Incorrect Test Selection

Choosing the wrong statistical test can lead to incorrect conclusions. Ensure you understand the assumptions of each test and select the one that best fits your data and research question.
Solution:
Carefully review the assumptions of each test and consult with a statistician if needed.

7.2 Ignoring Assumptions

Violating the assumptions of a statistical test can invalidate your results.
Solution:
Verify that your data meets the assumptions of the chosen test. Use data transformations or non-parametric tests if assumptions are violated.

7.3 Overinterpreting Results

Statistical significance does not always imply practical significance.
Solution:
Consider the magnitude of the effect and its real-world implications.

7.4 Data Dredging

Data dredging, also known as p-hacking, involves repeatedly testing different hypotheses until a significant result is found.
Solution:
Define your research question and hypotheses before analyzing the data. Avoid running multiple tests without proper justification.

7.5 Sample Size Issues

Small sample sizes can lead to low statistical power, making it difficult to detect real differences.
Solution:
Ensure you have an adequate sample size to detect meaningful effects. Perform a power analysis to determine the required sample size.

7.6 Ignoring Outliers

Outliers can disproportionately influence statistical results.
Solution:
Identify and address outliers appropriately. Consider using robust statistical methods that are less sensitive to outliers.

7.7 Data Entry Errors

Inaccurate data entry can lead to misleading results.
Solution:
Implement data validation procedures to minimize errors. Double-check your data for accuracy.

7.8 Confounding Variables

Failing to account for confounding variables can lead to spurious associations.
Solution:
Identify potential confounding variables and control for them in your analysis.

8. Advanced Techniques in Statistical Data Comparison

For more complex analyses, consider advanced statistical techniques that provide deeper insights and address specific challenges.

8.1 Regression Analysis

Regression analysis is used to model the relationship between a dependent variable and one or more independent variables. It can be used to predict outcomes and understand the factors that influence them.
Applications:

Predicting sales based on marketing spend.
Analyzing the impact of education on income.

8.2 Multivariate Analysis

Multivariate analysis involves analyzing multiple variables simultaneously. Techniques such as principal component analysis (PCA) and factor analysis can be used to reduce the dimensionality of the data and identify underlying patterns.
Applications:

Analyzing customer behavior based on multiple demographic and psychographic variables.
Identifying key factors that contribute to employee satisfaction.

8.3 Time Series Analysis

Time series analysis is used to analyze data points collected over time. It can be used to identify trends, patterns, and seasonal variations.
Applications:

Forecasting sales.
Analyzing stock market trends.

8.4 Bayesian Statistics

Bayesian statistics involves updating probabilities based on new evidence. It provides a flexible framework for incorporating prior knowledge and beliefs into statistical analysis.
Applications:

Clinical trial analysis.
Risk assessment.

8.5 Machine Learning Techniques

Machine learning techniques such as clustering, classification, and anomaly detection can be used to identify patterns and relationships in large data sets.
Applications:

Customer segmentation.
Fraud detection.

9. Tools and Software for Statistical Data Comparison

Several tools and software packages are available to assist with statistical data comparison, each with its own strengths and features.

9.1 R

R is a free, open-source programming language and software environment for statistical computing and graphics. It offers a wide range of statistical packages and is highly customizable.
Pros:

Free and open-source.
Extensive statistical packages.
Highly customizable.
Cons:
Steeper learning curve.

9.2 Python

Python is a versatile programming language with powerful libraries for data analysis and machine learning, such as NumPy, pandas, and scikit-learn.
Pros:

Versatile and easy to learn.
Powerful data analysis libraries.
Widely used in data science.
Cons:
Requires some programming knowledge.

9.3 SPSS

SPSS (Statistical Package for the Social Sciences) is a user-friendly statistical software package commonly used in the social sciences.
Pros:

User-friendly interface.
Wide range of statistical procedures.
Good for beginners.
Cons:
Commercial software (requires a license).

9.4 SAS

SAS (Statistical Analysis System) is a comprehensive statistical software suite used in various industries, including healthcare and finance.
Pros:

Powerful statistical capabilities.
Good for large data sets.
Used in many industries.
Cons:
Commercial software (requires a license).

9.5 Excel

Excel is a widely used spreadsheet program with basic statistical functions. It can be useful for simple data comparisons.
Pros:

Widely available.
Easy to use for basic tasks.
Cons:
Limited statistical capabilities.
Not suitable for complex analyses.

10. Case Studies: Successful Applications of Statistical Data Comparison

Examining real-world case studies demonstrates the practical value of statistical data comparison.

10.1 Healthcare: Comparing Treatment Effectiveness

Scenario:
Researchers want to compare the effectiveness of two different treatments for a specific medical condition.
Methods:

Collect data on patient outcomes (e.g., recovery rates, symptom reduction) for both treatment groups.
Use t-tests or Mann-Whitney U tests to compare the outcomes.
Perform regression analysis to control for confounding variables.
Results:
The statistical analysis identifies whether one treatment is significantly more effective than the other, leading to better patient care.
Impact:
Improved treatment protocols and better patient outcomes.

10.2 Marketing: Evaluating Campaign Performance

Scenario:
A marketing team wants to evaluate the performance of two different advertising campaigns.
Methods:

Collect data on key metrics (e.g., click-through rates, conversion rates, sales) for both campaigns.
Use t-tests or ANOVA to compare the metrics.
Perform A/B testing to optimize campaign performance.
Results:
The statistical analysis determines which campaign is more effective, allowing the team to allocate resources accordingly.
Impact:
Increased marketing ROI and improved campaign effectiveness.

10.3 Education: Assessing Teaching Methods

Scenario:
Educators want to assess the effectiveness of two different teaching methods on student performance.
Methods:

Collect data on student test scores for both teaching methods.
Use t-tests or ANOVA to compare the scores.
Perform regression analysis to control for student demographics and prior academic performance.
Results:
The statistical analysis identifies which teaching method leads to better student outcomes, informing pedagogical practices.
Impact:
Improved teaching strategies and enhanced student learning.

10.4 Finance: Analyzing Investment Strategies

Scenario:
Financial analysts want to compare the performance of two different investment strategies.
Methods:

Collect data on investment returns, risk metrics, and market conditions for both strategies.
Use t-tests or regression analysis to compare the performance.
Perform time series analysis to identify trends and patterns.
Results:
The statistical analysis determines which investment strategy provides better returns and manages risk more effectively.
Impact:
Informed investment decisions and improved portfolio performance.

[

11. Ethical Considerations in Statistical Data Comparison

Ethical considerations are paramount when comparing data sets to ensure fairness, transparency, and respect for individuals and communities.

11.1 Data Privacy and Confidentiality

Protect the privacy and confidentiality of individuals when using personal data.
Best Practices:

Obtain informed consent from participants.
Anonymize or de-identify data to prevent re-identification.
Comply with relevant data protection regulations (e.g., GDPR, CCPA).

11.2 Avoiding Bias

Minimize bias in data collection, analysis, and interpretation.
Best Practices:

Use representative samples.
Control for confounding variables.
Be transparent about limitations and potential biases.

11.3 Transparency and Reproducibility

Ensure transparency and reproducibility in your statistical analyses.
Best Practices:

Document all steps of the analysis process.
Share data and code when possible.
Use established statistical methods and report results accurately.

11.4 Fair Use of Results

Use statistical results responsibly and avoid misrepresenting or exaggerating findings.
Best Practices:

Clearly communicate the limitations of the analysis.
Avoid drawing causal conclusions without sufficient evidence.
Consider the potential impact of your findings on different groups.

11.5 Informed Consent

Obtain informed consent from participants before collecting or using their data.
Best Practices:

Explain the purpose of the research.
Describe the data collection methods.
Inform participants of their rights (e.g., to withdraw from the study).

11.6 Data Security

Ensure the security of data to prevent unauthorized access or misuse.
Best Practices:

Use secure data storage systems.
Implement access controls.
Train personnel on data security protocols.

12. Future Trends in Statistical Data Comparison

The field of statistical data comparison is continuously evolving with advancements in technology and methodologies.

12.1 Big Data Analytics

The increasing availability of large data sets is driving the development of new statistical methods for analyzing complex data.
Trends:

Scalable statistical algorithms.
Distributed computing.
Real-time data analysis.

12.2 Artificial Intelligence (AI) and Machine Learning (ML)

AI and ML techniques are being used to automate statistical analysis, identify patterns, and make predictions.
Trends:

Automated data preprocessing.
Machine learning-based statistical tests.
Explainable AI (XAI) for understanding model predictions.

12.3 Cloud Computing

Cloud computing provides access to powerful computing resources and statistical software, making it easier to analyze large data sets.
Trends:

Cloud-based statistical platforms.
Collaborative data analysis.
Secure data storage and sharing.

12.4 Advanced Visualization Techniques

Advanced visualization techniques are being used to communicate statistical results more effectively.
Trends:

Interactive dashboards.
3D visualizations.
Virtual reality (VR) data exploration.

12.5 Interdisciplinary Collaboration

Statistical data comparison is becoming increasingly interdisciplinary, with collaborations between statisticians, data scientists, and domain experts.
Trends:

Cross-functional teams.
Integration of statistical methods with domain knowledge.
Development of customized statistical solutions.

FAQ: Statistical Data Comparison

1. What is the first step in comparing two data sets statistically?

The first step is to define your research question clearly. This will guide your choice of statistical methods and interpretation of results.

2. How do I choose the right statistical test for my data?

Choose a statistical test based on the type of data (continuous, categorical), the distribution of the data (normal, non-normal), and the research question.

3. What is a p-value, and how is it used in statistical data comparison?

The p-value is the probability of obtaining results as extreme as, or more extreme than, the observed results, assuming that the null hypothesis is true. It is used to determine the statistical significance of results. A small p-value (typically ≤ 0.05) indicates strong evidence against the null hypothesis.

4. What are some common pitfalls to avoid when comparing data sets statistically?

Common pitfalls include incorrect test selection, ignoring assumptions, overinterpreting results, data dredging, and sample size issues.

5. How can I ensure that my statistical data comparison is ethical?

Ensure ethical data comparison by protecting data privacy, avoiding bias, ensuring transparency, using results fairly, obtaining informed consent, and ensuring data security.

6. What is the difference between a t-test and a Mann-Whitney U test?

A t-test is used to compare the means of two groups and assumes that the data is normally distributed. The Mann-Whitney U test is a non-parametric test used to compare two groups when the data is not normally distributed.

7. What software can I use for statistical data comparison?

Common software options include R, Python, SPSS, SAS, and Excel.

8. How can I control for confounding variables in my analysis?

Control for confounding variables by using regression analysis or other statistical techniques that allow you to adjust for the effects of these variables.

9. What is regression analysis, and how is it used in data comparison?

10. What future trends are shaping the field of statistical data comparison?

Future trends include big data analytics, AI and machine learning, cloud computing, advanced visualization techniques, and interdisciplinary collaboration.

Conclusion

Statistically comparing two data sets is essential for making informed decisions, validating hypotheses, and improving processes. By understanding the key concepts, following the steps outlined in this guide, and avoiding common pitfalls, you can conduct accurate and meaningful comparisons. Whether you’re using t-tests, Mann-Whitney U tests, or more advanced techniques, the goal is to gain insights that drive better outcomes.

Ready to take your data comparison skills to the next level? Visit COMPARE.EDU.VN for more in-depth guides, tools, and expert advice. Make smarter decisions with confidence.

Address: 333 Comparison Plaza, Choice City, CA 90210, United States
WhatsApp: +1 (626) 555-9090
Website: compare.edu.vn